图形学中常见的数学困惑

前言

我高中搞了三年数学竞赛，之前还对自己的数学能力很自负，现在发现自己太naive了。在学习图形学的过程中就遇到了不少困惑，有的当时搞明白了过后又忘记了，发现自己实在是太笨了，还是要好好记录总结一下。

这里主要是图形学中的线性代数部分总结整理，全局光照技术等部分或许会在以后整理。

这其中有很多是我自己的思考，比如旋转矩阵为什么单单绕y轴是反的，比如旋转矩阵另推与涉及的初等变换，比如内旋的yxz顺序为什么和外旋的zxy顺序是一样的。这里分享出来，主要也是自己的学习笔记总结，也希望能有大佬指正。

左右手系与旋转方向

先给出判断方法：通过叉乘去判断。

拿到一个三维坐标系xyz，用右手去做叉乘，如果 x 叉乘 y 的结果是 z 轴正半轴，就是右手系。如果是 z 轴负半轴，就是左手系。

左右手系有一种常见的判断方法（但是我从没有用过这种方法）：

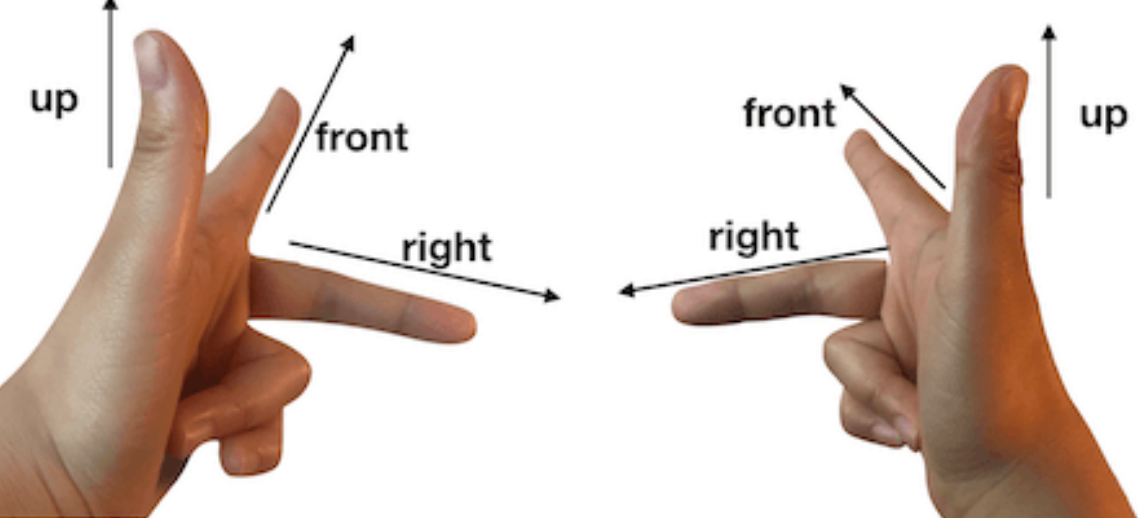
比如拿到一个三维坐标系xyz，用右手去做叉乘：

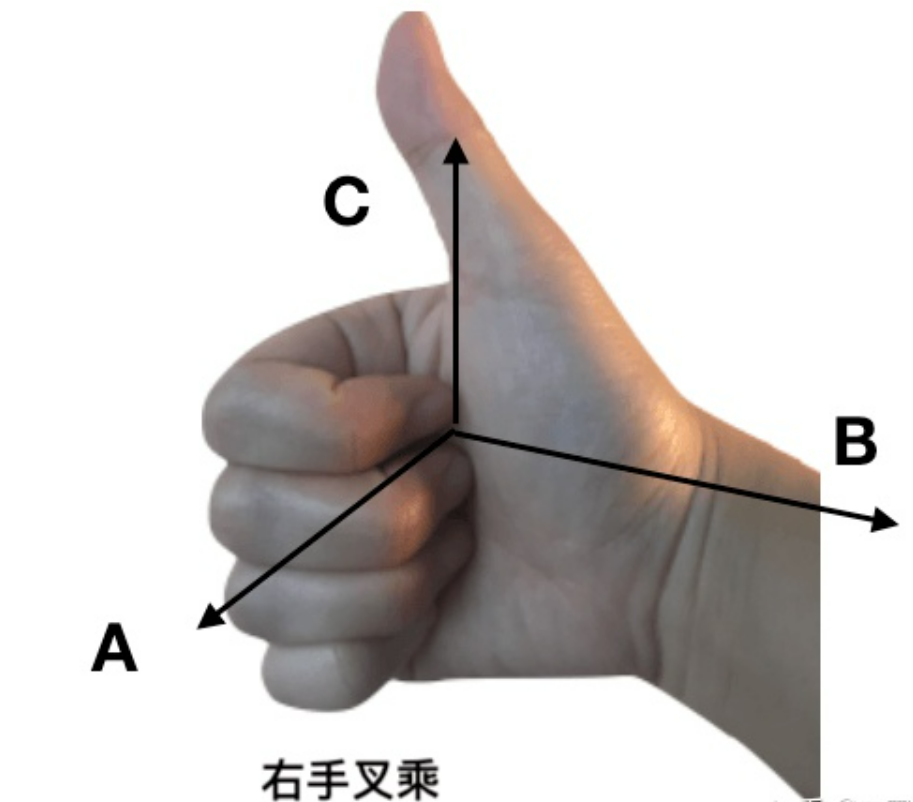
如果 x 叉乘 y 的结果是 z 轴正半轴，就是右手系。如果是 z 轴负半轴，就是左手系。

但是事实上，左手系和右手系的叉乘是不一样的：左手系是用左手去判断，右手系则是用右手去判断。

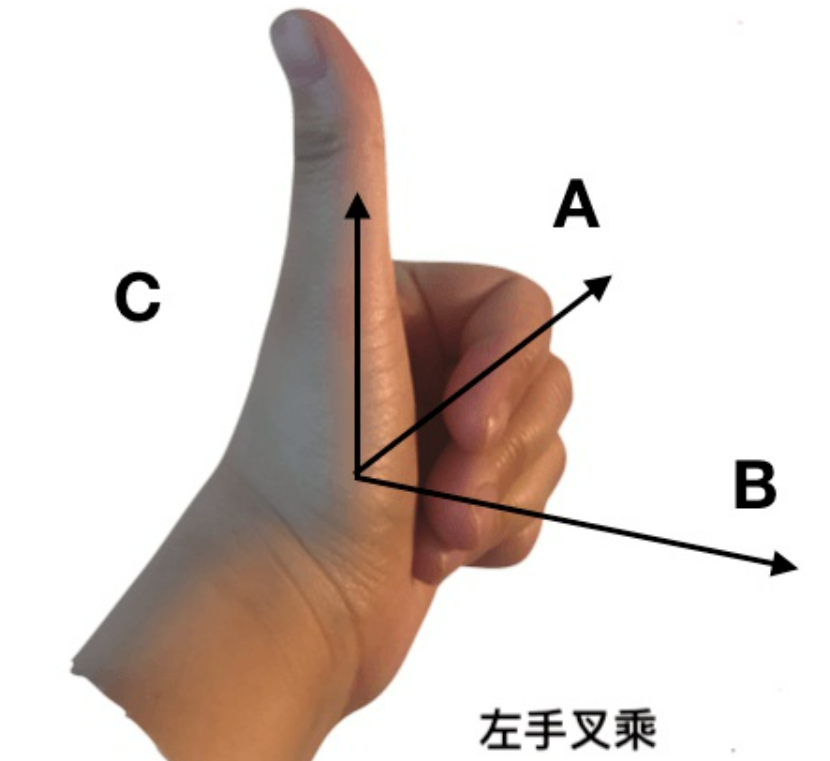
但是叉乘的公式都是一样的，为了方便记忆可以借助行列式：
$$w=u\times v=(u_y{v}_z-u_z{v}_y,u_z{v}_x-u_x{v}_z,u_x{v}_y-u_y{v}_x)=\left|\begin{array}{ccc}i& j& k\\ u_x& u_y& u_z\\ v_x& v_y& v_z\end{array}\right|$$

这部分的示意图源自：https://zhuanlan.zhihu.com/p/64707259

因此左右手系的几个特点：

1. 叉乘公式是一样的

2. 左手系叉乘用左手，右手系叉乘用右手，判断统一先用右手叉乘试一试

3. 旋转的正方向，左手系用左手判断，右手系用右手判断（和叉乘判断类似，伸出大拇指让它指向旋转轴正方向，那么旋转的正方向就是剩下4个手指的弯曲方向）

常用软件使用的坐标系（这张图的出处我不记得了）：
·
这里补充一下，Unity使用的是左手坐标系，但是对于观察空间（即以摄像机为原点的坐标系）则是右手坐标系。

旋转矩阵为什么单单绕y轴是反的

这里我们都考虑矩阵左乘的情况，即对应行变换，下同。


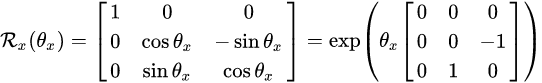
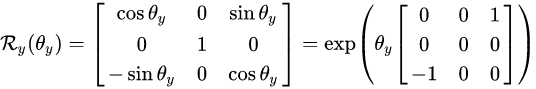
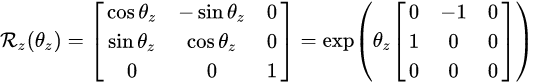
公式懒得敲了，之间从维基百科复制了：
https://zh.wikipedia.org/wiki/%E6%97%8B%E8%BD%AC%E7%9F%A9%E9%98%B5

这里还要明确一下，一般矩阵是左乘，即对应是行变换。而在如D3D的龙书中，所有的矩阵都是右乘，对应则是进行列变换。那么对于矩阵A 乘以一个向量 v， 其转置就是 向量v的转置乘以矩阵A的转置。

因此有的地方看到旋转矩阵是上面三个公式的转置，对应则应该是矩阵右乘的情况。

然而无论是哪种情况，都看到一个神奇的现象，就是它们单单绕y轴是反着的，其实原因很简单：

我在前面说了旋转方向是根据坐标系按照左右手去进行判断。这里便于理解以右手系为例，并且给一张坐标系的图片（首先复习一下，这里用右手去叉乘，x 叉乘 y 的结果为 z 轴正半轴， 所以给的是右手系的图片）：

绕x轴旋转的时候，对应右手4个手指的弯曲方向从y到z；绕z轴旋转的时候，对应右手4个手指的弯曲方向从x到y；

但是注意，绕y轴旋转的时候，对应旋转方向是从z到x。

而我们对于三维矩阵的推导一般是在二维平面上进行的，这是因为绕某个轴旋转，其实是对应一个点的坐标在垂直于该轴的平面去进行旋转。而二维旋转的推导我们都是以xy平面、yz平面、xz平面去进行的，那么对于从z到x（即zx平面）则会变成相应矩阵的转置（因为旋转矩阵是正交阵，转置即为逆，xz平面逆时针转就等于zx平面顺时针转，所以表现出来是逆矩阵），因此表现出来只有旋转矩阵是反着的。

旋转矩阵的另推

这里先介绍错切矩阵：

说到矩阵一定要谈到矩阵的三种初等变换，但是我发现大多图形学书籍都不会涉及到。从百度百科复制来的定义：

所谓数域P上矩阵的初等行变换是指下列3种变换：

1）以P中一个非零的数乘矩阵的某一行

2）把矩阵的某一行的c倍加到另一行，这里c是P中的任意一个数

3）互换矩阵中两行的位置

可以看到，所谓错切矩阵其实就是上述变换中的2. 而所谓缩放就是上述变换中的1. 所谓平移则是齐次坐标下的2.

那么所谓旋转对应什么初等变换呢？这里给出我个人的思考：所谓旋转其实是错切和缩放的结合，即1和2两种初等变换的组合。证明很简单，比如我随手画一个图：

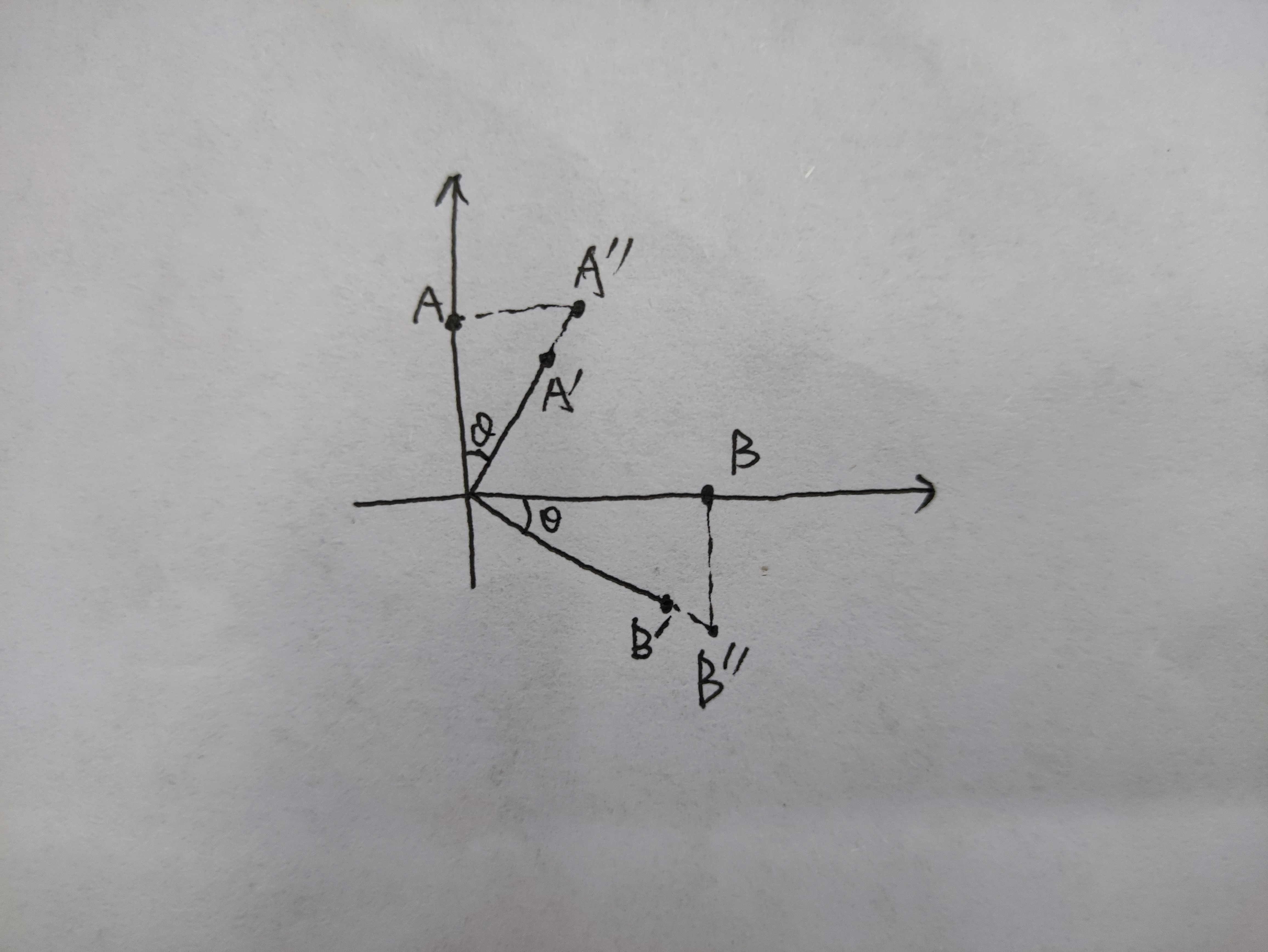
对于A、B两点，可以由错切矩阵得到 A’’ 和 B’’ ，再有缩放矩阵得到 A’ 和 B’，对应的矩阵为：
$$Shear=\left[\begin{array}{ccc}1& tan\theta & 0\\ -tan\theta & 1& 0\\ 0& 0& 1\end{array}\right],Scale=\left[\begin{array}{ccc}cos\theta & 1& 0\\ 0& cos\theta & 0\\ 0& 0& 1\end{array}\right]$$

同时，由于旋转矩阵可以看成是坐标系的变换（后续会提到），因此考虑A、B两点（或OA、OB两向量）已足够。

先旋转再平移和先平移再旋转

一般对于变换的复合，我们遵循SRT原则：即先缩放Scale，再旋转Rotate，最后平移Translate。

一般接触图形学都会说先旋转再平移和先平移再旋转是两码事。但是这里从数学角度来看更恰当。

首先从维基百科抄一下线性变换和仿射变换的定义：


因此可以看到，引入齐次坐标有一个很大的用处就是方便定义平移矩阵。

再对于旋转矩阵：

绕任意轴的非齐次坐标矩阵：

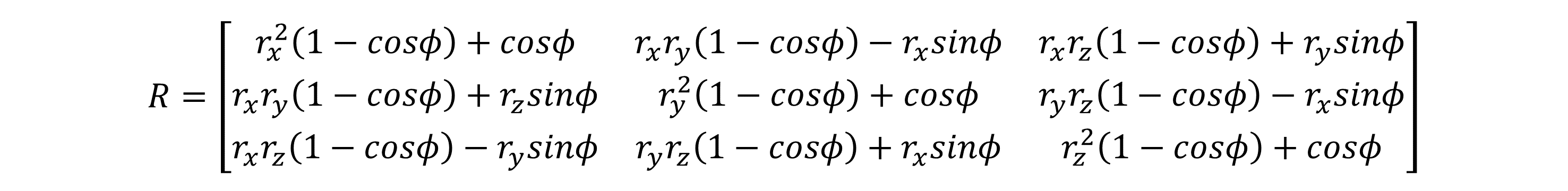
绕x、y、z轴的齐次坐标矩阵：

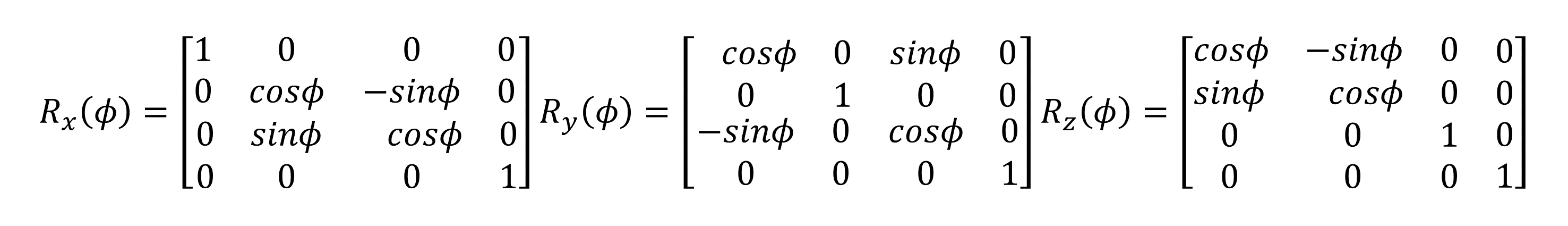
而平移变换的矩阵：

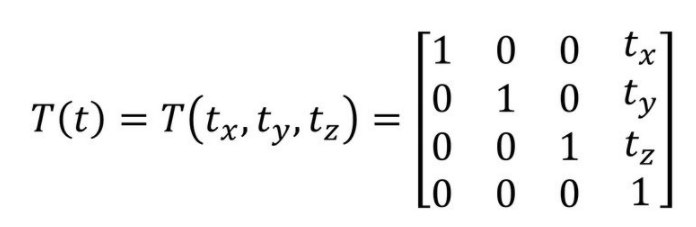
之前已经说了初等变换，可以看到齐次坐标下的平移变换都是针对第四行进行第二种初等变换，而在SRT中第四行固定为 (0, 0, 0, 1)。

因此显而易见先平移后旋转和先旋转后平移他们的矩阵都是不一样的，严格遵照SRT原则，平移矩阵得到的结果（即第二种初等变换：把矩阵的某一行的c倍加到另一行）就不会受到前面S和R的缩放影响，即最终矩阵第四列依然是tx ty tz； 因此现在大多采用SRT原则的方式。

旋转的两种视角

接下来这一块参考了这个博客：https://blog.csdn.net/hzwwpgmwy/article/details/101547949

不过主要还是自己的一个思考。

事实上不光是旋转矩阵，任何一个仿射变换（缩放、旋转、平移）都有两种视角去解读：

1. 使几何体本身发生变换。

2. 看成是坐标系的变换。

就比如绕x轴旋转30度这样一个旋转矩阵，既可以看作对于一个场景，这个场景绕x轴逆时针旋转30度； 也可以看作对于整个坐标系，整个坐标系绕x轴顺时针旋转30度。

对于一个原坐标系中的点p，旋转矩阵R，变换后为：
$$p^{\prime }=R\ast p$$

p’ 为变换后的点在原坐标系的位置。

两边取逆有公式：
$$R^T\ast p^{\prime }=p$$

比如 R 是绕着轴 t 逆时针旋转α角度，那么$R^T$ 就是绕着轴ｔ顺时针旋转α角度。因此上述公式可以看成：原坐标系绕着轴ｔ顺时针旋转α角度得到新的坐标系，点ｐ在新的坐标系下的表示为 p’

欧拉角内旋、外旋与万向节死锁

欧拉角经典图片和GIF：
https://en.wikipedia.org/wiki/Euler_angles


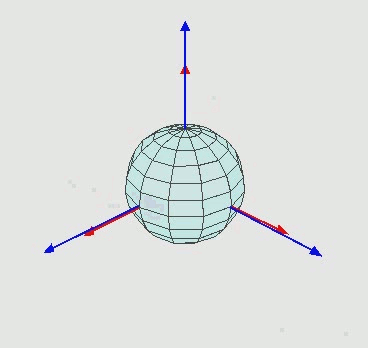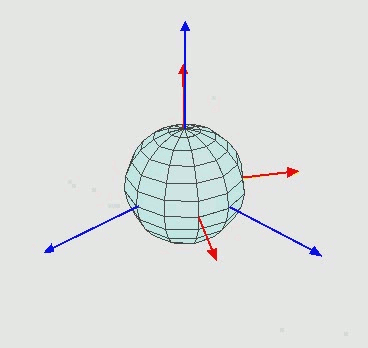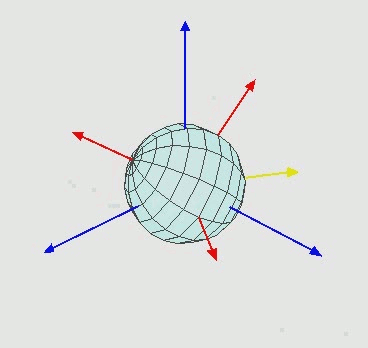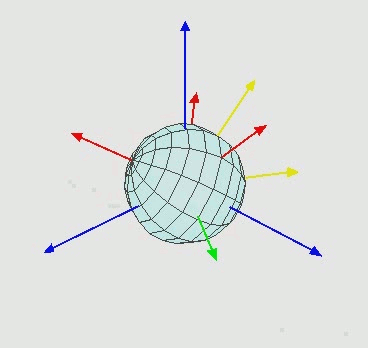
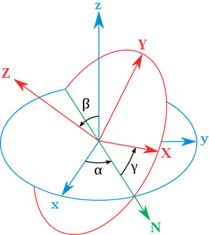
实际上欧拉角是区分内旋和外旋的，又或者叫动态欧拉角与静态欧拉角。

内在旋转（内旋， 或叫动态欧拉角）每次旋转围绕的轴是上次旋转之后坐标系的某个轴，外在旋转（外旋， 或叫静态欧拉角）每次旋转的轴是固定坐标系中的轴。

首先来看最简单的外旋（确实是懒得扣latex，我厚颜无耻地直接从鸡哥那里截图了）：
https://zhuanlan.zhihu.com/p/45404840

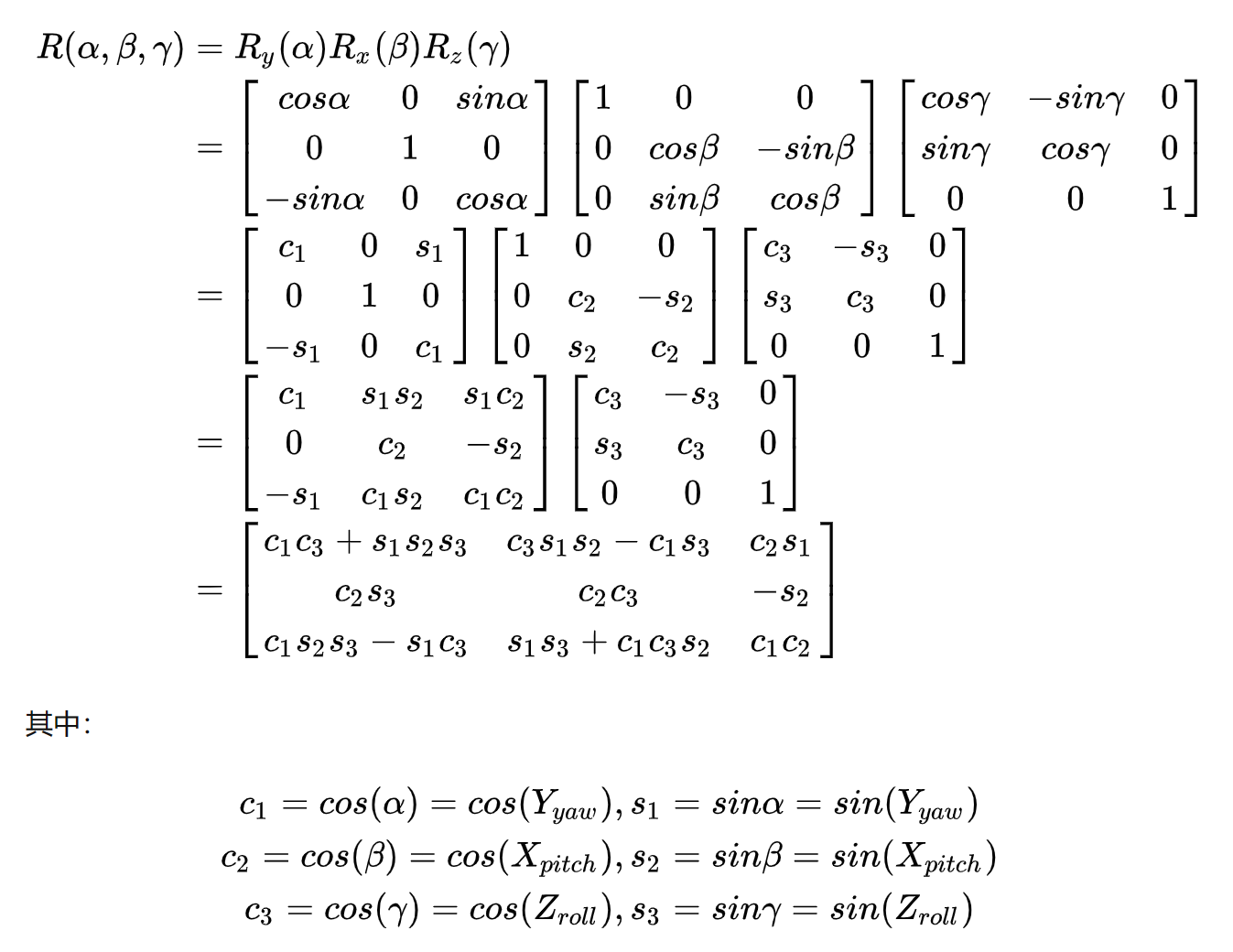
毕竟是绕世界坐标系ｚｘｙ轴，我们直接按顺序乘就好了，这个很容易理解。

再来说内旋，思考一下如何表示内旋中的坐标轴叠加的一个关系，可以想到，我们可以按照把一个旋转矩阵看成是坐标系的变换的角度去理解，这样就顺理成章叠加起来了：

同样是绕ｚｘｙ轴，根据我之前所说的旋转的两种视角那一块的公式，那么内旋的表示就是：

$$R_y^T{R}_x^T{R}_z^T{p}^{\prime }=p$$

那么对应的p’点的坐标就是在两边取对应矩阵的逆即可：

$$p^{\prime }=R_z{R}_x{R}_{y}p$$

对比一下内旋外旋，因此我们发现这样的结论：

内旋的ｙｘｚ顺序与外旋的ｚｘｙ顺序是一致的。即把旋转顺序颠倒一下，得到的结果就是一样的。

顺便多提一句，unity文档中说明的旋转顺序指的是静态的，即旋转时坐标系不会跟着旋转。

最后说一下万向节死锁，似乎很多人被绕进去了，甚至还看到过很多篇专栏专门讲为什么会产生万向节死锁，但其实原理应该很简单：

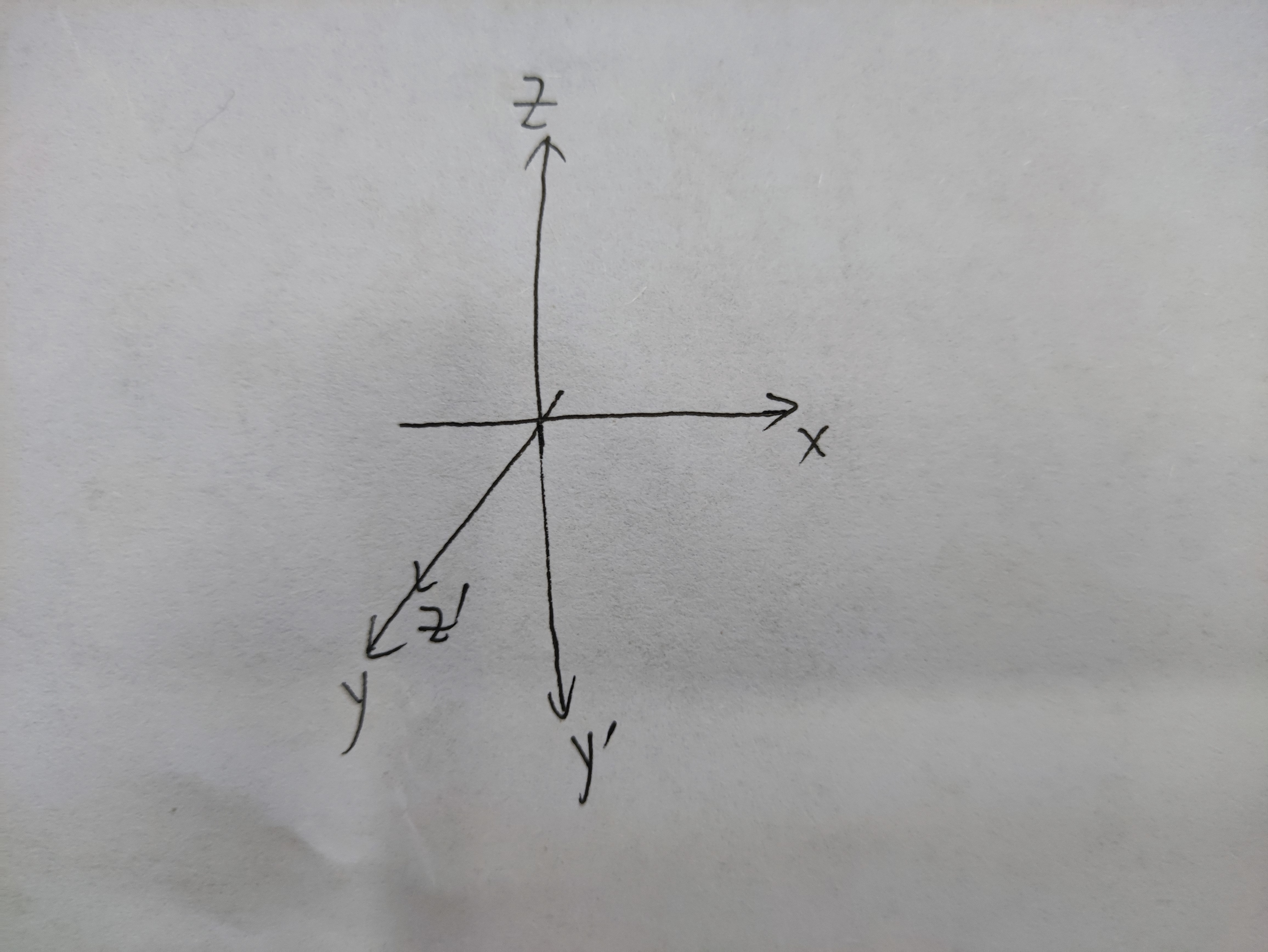
比如就拿z x y顺序来看，如果绕ｘ轴旋转90度的话，如下图是所示，ｙ轴变成了 y’ 轴，z 轴变成了 z’ 轴，而 y’ 轴如图其实就是原来的z轴负半轴，因此之后再绕y轴旋转和在一开始绕z轴旋转没任何差别，少了一个自由度，称为万向节死锁。

参考

https://blog.csdn.net/hzwwpgmwy/article/details/101547949

其他一些写的不错的博客：
https://zhuanlan.zhihu.com/p/80852438
https://zhuanlan.zhihu.com/p/356878461
https://zhuanlan.zhihu.com/p/45404840