【模型预测控制MPC】：深蓝路径规划课程P8笔记

后厂村路钢铁侠

已于 2023-10-20 10:17:18 修改

阅读量1.9k

点赞数 6

分类专栏：深蓝路径规划作业路径规划算法文章标签：算法机器人无人机动态规划

于 2023-10-18 15:58:49 首次发布

本文链接：https://blog.csdn.net/weixin_47765522/article/details/133894400

版权

深蓝路径规划作业同时被 2 个专栏收录

8 篇文章

订阅专栏

路径规划算法

3 篇文章

订阅专栏

简介：模型预测控制在机器人学的应用，涉及线性MPC、非线性MPC以及粒子群优化算法的JLT问题求解。

P7课程笔记：基于马尔可夫决策过程的运动规划-深蓝路径规划P7笔记-CSDN博客

作业代码实现：【MPC】追踪锥形螺旋：深蓝路径规划课程P8作业-CSDN博客

一、引言

1.1名词解释

模型预测控制可以分别从三个关键词来看：

模型（moodel）：主要分为两个，一个是问题模型，一个是系统模型，以经典的小球运动为例，f=ma就是系统模型，最下化当前位置和目标位置的差就是问题模型。

预测（prediction）：包含三个内容：输入、其他状态，参数空间，比如外力就是输入，其他状态包括速度、加速度、位置等，那参数空间是什么呢？参数空间是为了把力的未来的状态（无限个，不可解）转化为一个多项式描述，这个多项式的参数是有限个的，是可以描述的，称为参数空间。这样在后面优化问题模型就可以只优化多项式的参数即可。

参数空间的常用处理方式有：zero order hold（离散采样）、多项式（Polynomial）、贝塞尔曲线（B-spline）、基于机器学习的方法。

控制（control）：在参数空间里面选择一个最优的参数组合。

1.2优化函数建模

目标函数：对一般的问题优化的目标函数主要分为final cost：关注最后tf时刻的状态和running cost：关注t0-tf期间的消耗。

约束条件分为四部分：动力学约束、不等式约束（最大速度限制、最大加速度限制、高度限制）、等式约束（起始点和终止点的参数）和障碍物避免约束（防止轨迹进入障碍物内，往往是非凸的，需要进行特殊处理）。

优化目标：通过在参数空间内找到最佳的u使得目标函数最小化。

优化方法：搜索（图搜索、随机搜索）、凸优化（二次规划）、非凸优化（SQP、Particle swarm optimization），标红的部分是采用的方案。

1.3 Tube Based MPC整体流程

在经典的Control模型中，通过优化解出u*，带入到系统里执行，然后通过观测再解出新的u*',这样的方式存在的问题是，优化的频率太低，无法跟随控制系统的频率（大概是200-1000hz）。于是引出了Tube Based MPC，实现不同频率模块的解耦：

外环：低频控制模型中的X*;

内环：高频跟踪外环优化出的轨迹。

可以选用MATLAB MPC toolbox、μAO-MPC、Acado toolkit、YANE、Multi-Parametric Toolbox 3等软件求解建模。

二、线性MPC

2.1基本模型

系统建模：一般是根据动力学模型，预测未来的4s，离散成20份，每份dt0.2s，通过矩阵可以描述预测模型PVA，以及参数空间J。每当选定有一定的参数后，就可以预测未来的PVA。

问题建模：

目标①：PVA终点都为0；

目标②：轨迹光滑，减少输入幅值。

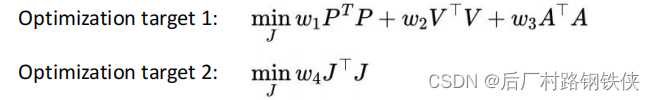
问题求解：

可结合起来写，可以将问题转化为二次规划问题，利用MATLAB中的quadprog求解，其中Bp、Bv、Ba是和初始状态相关的函数：

2.2包含不等式约束

2.2.1常规解法

比如说对速度v和加速度a约束其范围在[-1,,1]之间，

$\begin{aligned}&-1\leq v_i\leq1,\forall i\in\{1,2,3\cdots,20\};&-1\leq a_i\leq1,\forall i\in\{1,2,3,\ldots,20\}\end{aligned}.$

写出矩阵形式为以下形式：

$\begin{aligned}-1_{20\times1}&\le V\le1_{20\times1}\\-1_{20\times1}&\le A\le1_{20\times1}\end{aligned}$

其中 $V=T_vJ+B_v$ ， $A=T_aJ+B_a$ ，把不等式拆开带入后写成小于等于的形式（quadprog求解器的要求）：

2.2.2软约束的解法

但是在一些特定的情况，没有解：比如你要求速度从12m/s降到1m/s，但是你预测的时长只有4s，这明显是无解的。于是又两种解决手段：①是增大你的预测时间，这样会带来计算量上升，但是对系统正定是有益的；②采用软约束（soft constraints）的方法，将不等式转化为惩罚项带入目标函数中。

一般来说，对输入的不等式可以采用软约束，输出的不等式采用硬约束（避免机械损伤等）。

于是引入参数L，以速度的约束为例：

$\begin{aligned}&-T_vJ\leqslant1_{20\times1}+B_v+L\\&-L\leqslant0\\&L=[l,l_2,l_3,\cdots,l_{20}]^\top\end{aligned}$

当L足够大的时候，这个式子是一定满足的；但是太大的话会导致这个式子没有含义了，于是在目标函数中加入对L的约束，限制其过大，一般会把该项惩罚系数w5设置的很大：

$\begin{aligned}\min_{J,L}w_1P^TP+w_2V^\top V+w_3A^\top A+w_4J^\top J+w_5L^\top L\end{aligned}$

这个式子同样可以利用二次规划的方式进行求解，这种方法的优势是会对违反约束条件的状态更加鲁棒。

示例代码解读：

2.3线性MPC的缺陷

①要求系统模型是线性的或者是被线性化的。

②对障碍物处理不理想。障碍物通常是凸的，但是可通行区域不是凸的。需要利用许多“或”进行表示，而非凸的优化问题对初值比较敏感。

三、非线性MPC

非线性MPC最终都是要回归到线性MPC上。

3.1BSCP

Boundary constrained motion primitives (BSCP)与多项式参数空间、采样（Zero order hold）参数空间不同，是以系统初始状态和系统期望达到的状态作为参数空间的参数的，放到两点编织问题中求解，对比如下：

以JLT（加加速度jerk限制轨迹）为例，其优势是：连续变化的力，没有跳变，对机械结构比较友好，被广泛应用于机器人领域，以四旋翼模型为例：

①四旋翼只受两个力：升力和重力，但 升力是有限制的，以及body rate： $\omega$ 也是有限制的。

②规划是在外环中的，限制①是内环信息，需要利用公式将 内环映射到外环中。如左下角的框内公式所示：公式1约束了加加速度，公式2、3约束力加速度。

③上述公式是非线性的，需要转化为线性问题，采用对幅值约束，②中三个公式就能满足要求。

④出于安全考虑，还需要考虑最大速度限制。

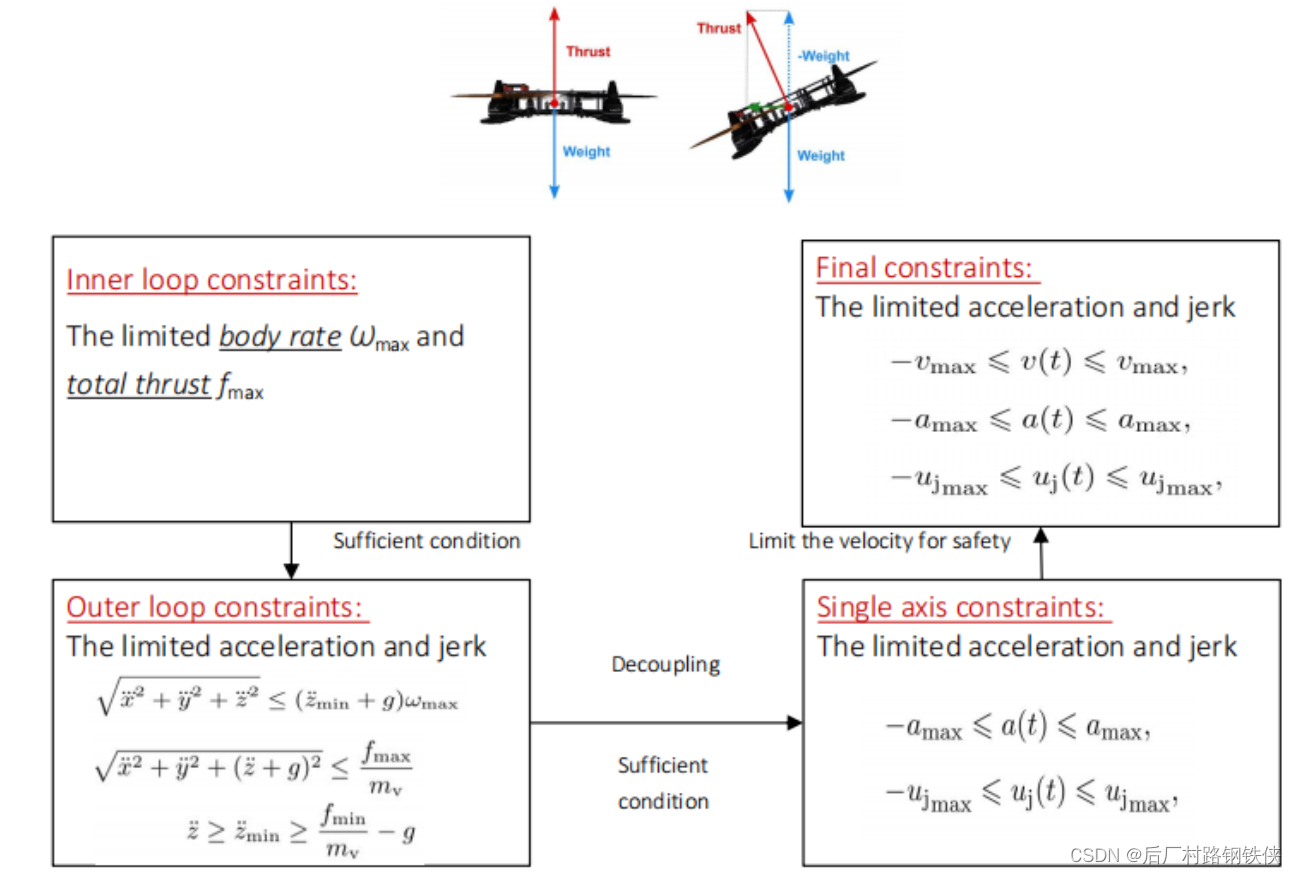
3.2Jerk limited trajectory

二阶积分器模型：

$\begin{aligned} &\begin{aligned}v(0)=v_0,\quad v(T)=v_{\text{ref}}\end{aligned}&&& \\ &\begin{aligned}a(0)=a_0,\quad a(T)=0\end{aligned} \\ &\begin{aligned}\dot{v}(t)=a(t)\end{aligned} \\ &\begin{aligned}\dot{a}(t)=u_j(t)\end{aligned} \\ &\begin{aligned}-a_{\max}\leqslant a(t)\leqslant a_{\max},\quad\forall t\in[0,T]\end{aligned} \\ &\begin{aligned}-u_\mathrm{jmax}\leqslant u_\mathrm{j}(t)\leqslant u_\mathrm{jmax},&\forall t\in[0,T]\end{aligned} \end{aligned}$

这是一个二阶积分器的模型，输入不仅有加速度a，还有加加速度jerk的限制，而且还有状态上的幅值限制。最后加加速度一般是三种情况，①最大jmax②最小jmin③0。那么加速度就会是三角形或者是梯形，那么与坐标轴围成的面积就是变化速度ΔV。先然他加速到最大加速度amax度再下降到0，那么根据现有的三角形覆盖面积比较目标的V，求解是一个分类情况讨论的问题：

①面积太大了，缩小面积，让他上升一个t1后下降到0.（如左图）

②面积太小了，让它变成一个梯形，增加的是一个长方形，计算Δt2即可。（如右图）

三阶积分器模型：

$\begin{aligned} &p(0)=p_{0},\quad p(T) =p_{\mathrm{ref}} \\ &v(0)=v_{0},\quad v(T) =0 \\ &\begin{aligned}a(0)=a_0,\quad a(T)= 0 \end{aligned} \\ &\dot{p}(t)=v(t) \\ &\dot{v}(t)=a(t) \\ &\begin{aligned}\dot{a}(t)=u_j(t)\end{aligned} \\ &\begin{aligned}-v_{\max}\leqslant v(t)\leqslant v_{\max},\quad\forall t\in[0,T]\end{aligned} \\ &\begin{aligned}-a_{\max}\leqslant a(t)\leqslant a_{\max},\quad\forall t\in[0,T]\end{aligned} \\ &\begin{aligned}-u_{\mathrm{jmax}}\leqslant u_{\mathrm{j}}(t)\leqslant u_{\mathrm{jmax}},\forall t\in[0,T]\end{aligned} \end{aligned}$