电机驱动(二)——SVPWM

电机驱动(二)——SVPWM

version : v1.0 「2022.7.28」 最后补充


author： Y.Z.T.

摘要： 简要介绍FOC驱动从坐标变换到SVPWM 各个部分在MATLAB仿真和硬件平台实现的学习过程


备注： ❗️面向自己的笔记 , 有的地方可能说的不是很清晰

---

⭐️ 目录

3️⃣ SVPWM 控制流程

$$SVPWM\{\begin{array}{l}输入V_{\alpha }和V_{\beta }\\ 输出三相定时器的pwm\end{array}$$

控制流程:

①获取$V_{\alpha }$ 和 $V_{\beta }$

②根据$V_{\alpha }$ 和 $V_{\beta }$ 判断当前扇区

③计算相邻两个矢量 , 每个矢量的作用时长

④通过矢量作用时长计算出定时器的高电平时间

⑤通过定时器每个高电平时间计算出每个通道的CCR值

---

3.1 引入

• 首先我们需要在三相线圈里面产生正弦的交流电流 ,来产生旋转的磁场 , 进而控制转子的转动 ;
• 而三相正弦电流 由三相正弦电压产生 , 但是我们的供电是直流供电的方式
• 通过mos管控制 , 只有 通和不通两种状态 ， 所以通过平均值等效的方式, 将正弦波转换为pwm波
• 最终实现 , 通过直流mos管的开关 , 来模拟正弦的电压信号

正弦波转换成pwm波

用上面坐标系中的正弦波和三角波的交点投影到下面的坐标轴，以此确定PWM的占空比变化规律，这样合成的PWM波，经过低通滤波器之后，其实就等效为了一个正弦波

---

3.2 空间电压矢量

• 前面提到了6步换向的驱动方式 , 通过ABC三个桥臂的组合 , 总共有8个状态.
• 即有8个矢量方向, 通过相邻两个矢量的合成 , 就可以合成任意方向的矢量

3.2.1 等效电路

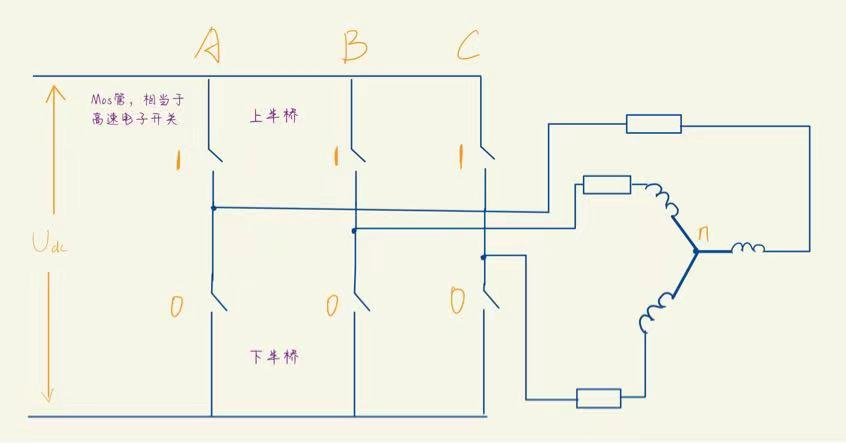
示例： 以(110) 和 (011)为例

---

3.2.2 八个矢量对应的电压关系

---

3.3.3合成矢量 $U$

三相电压矢量$U_a、U_b、U_c$ 合成矢量$U$

补充：

• 可以看到合成后的矢量的模是$U_{dc}$ , 但六个方向矢量的模却是 $\frac{2}{3}{U}_{dc}$
• 这是因为, 在从***x - y坐标系*** 等幅变换到*** $\alpha -\beta$ 坐标系***的过程中 , 进行了缩放 (即矢量长度缩小了1.5倍)
• 但是这种缩放 , 并不影响最后的占空比结果

---

3.3.4 小结

小结：

• 八个电压矢量中, 000和111 是零矢量 ;
• 其他6个矢量将整个空间划分成了6个扇区
• 为了减少管子在开关过程中的损耗 , 要保证每次都只改动一个桥臂的动作
• 所以六个矢量的大小都是 $\frac{2}{3}{V}_{dc}$

---

3.3 怎么合成任意向量

通过合理配置六个基向量 , 在一个PWM周期中的作用的时间 , 就能合成出任意的空间电压矢量

其中 :

• $U_{ref}$ 表示合成的空间电压矢量;
• $T_s$ 表示一个PWM的作用周期;
• $T_x$ 和 $T_y$ 分别表示$X方向矢量$ 和 $Y方向矢量$的作用时长

小结：

• $T_x$ 和 $T_y$ 的比值决定合成矢量的方向 ;

• 空矢量决定了力矩的大小;

• 当空矢量作用时间长的时候 , 合成矢量就小 , 电压就小 ; 电压小,电流也小 , 电机的扭矩就变小;

---

3.4 扇区判断

前面提到 , SVPWM的输入是$V_{\alpha }$ 和 $V_{\beta }$ , 我们需要通过$V_{\alpha }$ 和 $V_{\beta }$ 来获取角度信息, 进行扇区判断。

3.4.1 由$V_{\alpha }$ 和 $V_{\beta }$ 获取角度信息

ABC三相电压
$$\{\begin{array}{l}{V}_a=V_m\times \cos \theta \\ V_b=V_m\times \cos (\theta -\frac{2}{3}\pi )\\ V_b=V_m\times \cos (\theta +\frac{2}{3}\pi )\end{array}$$

• 其中 $V_m$ 为相电压有效值

$\alpha$ - $\beta$ 坐标系中 $V_{\alpha }$ 和 $V_{\beta }$ 表达式
$$\{\begin{array}{l}{V}_{\alpha }=V_a\cdot \cos 0^{\circ }-V_b\cdot \cos \frac{\pi }{3}-V_c\cdot \cos \frac{\pi }{3}\\ V_{\beta }=V_a\cdot \cos 90^{\circ }+V_b\cdot \cos \frac{\pi }{6}-V_c\cdot \cos \frac{\pi }{6}\end{array}$$

将ABC三相电压代入得
$$\{\begin{array}{l}{V}_{\alpha }=\frac{2}{3}{V}_m\cdot (cos\theta -\frac{1}{2}\cdot \cos (\theta -\frac{2}{3}\pi )-\frac{1}{2}\cdot \cos (\theta +\frac{2}{3}\pi )\\ V_{\alpha }=\frac{2}{3}{V}_m\cdot (\frac{\sqrt{3}}{2}\cdot \cos (\theta -\frac{2}{3}\pi )-\frac{\sqrt{3}}{2}\cdot \cos (\theta +\frac{2}{3}\pi )\end{array}$$

化简得
$$\{\begin{array}{l}{V}_{\alpha }=V_m\cdot \cos \theta \\ V_{\beta }=V_m\cdot \sin \theta \end{array}$$

提取出角度信息
$$\theta =\arctan (\frac{V_{\beta }}{V_{\alpha }})$$

---

3.4.2 扇区判断原理

扇区判断的原理是根据**矢量的角位置$\theta$**确定矢量在哪个区间

六个扇区对应的角度

扇区	角度	消除$\arctan$
I	$$0<\arctan (\frac{V_{\beta }}{V_{\alpha }})<60^{\circ }$$	$0<\frac{V_{\beta }}{V_{\alpha }}<\sqrt{3}$
II	$$60^{\circ }<\arctan (\frac{V_{\beta }}{V_{\alpha }})<120^{\circ }$$	$|\frac{V_{\beta }}{V_{\alpha }}|>\sqrt{3}$
III	$$120^{\circ }<\arctan (\frac{V_{\beta }}{V_{\alpha }})<180^{\circ }$$	$-\sqrt{3}<\frac{V_{\beta }}{V_{\alpha }}<0$
IV	$$180^{\circ }<\arctan (\frac{V_{\beta }}{V_{\alpha }})<240^{\circ }$$	$0<\frac{V_{\beta }}{V_{\alpha }}<\sqrt{3}$
V	$$240^{\circ }<\arctan (\frac{V_{\beta }}{V_{\alpha }})<270^{\circ }$$	$|\frac{V_{\beta }}{V_{\alpha }}|>\sqrt{3}$
VI	$$270^{\circ }<\arctan (\frac{V_{\beta }}{V_{\alpha }})<360^{\circ }$$	$-\sqrt{3}<\frac{V_{\beta }}{V_{\alpha }}<0$

由波形图像可获取$V_{\alpha }$ 和 $V_{\beta }$ 在各个扇区的值

汇总得

扇区	$V_{\beta }$值	$V_{\alpha }$值	代入$V_{\alpha }$和$V_{\beta }$ , 化简$\frac{V_{\beta }}{V_{\alpha }}$
I	$V_{\beta }$ > 0	$V_{\alpha }$ > 0	$\frac{V_{\beta }}{V_{\alpha }}<\sqrt{3}$
II	$V_{\beta }$ > 0	$V_{\alpha }$ > 0	$\frac{V_{\beta }}{|V_{\alpha }|}>\sqrt{3}$
III	$V_{\beta }$ > 0	$V_{\alpha }$ < 0	$\frac{V_{\beta }}{-V_{\alpha }}<\sqrt{3}$
IV	$V_{\beta }$ < 0	$V_{\alpha }$ < 0	$\frac{V_{\beta }}{V_{\alpha }}<\sqrt{3}$
V	$V_{\beta }$ < 0	$V_{\alpha }$ < 0	$\frac{V_{\beta }}{|V_{\alpha }|}>\sqrt{3}$
VI	$V_{\beta }$ < 0	$V_{\alpha }$ > 0	$\frac{-V_{\beta }}{V_{\alpha }}<\sqrt{3}$

进行不等式展开

扇区	$V_{\beta }$值(A相)	原不等式	展开 (B相)	(C相)
I	$V_{\beta }$ > 0	$$\frac{V_{\beta }}{V_{\alpha }}<\sqrt{3}$$	$\frac{\sqrt{3}}{2}{V}_{\alpha }-\frac{1}{2}{V}_{\beta }$ > 0	$-\frac{\sqrt{3}}{2}{V}_{\alpha }-\frac{1}{2}{V}_{\beta }$ < 0
II	$V_{\beta }$ > 0	$$\frac{V_{\beta }}{|V_{\alpha }|}>\sqrt{3}$$	$\frac{\sqrt{3}}{2}{V}_{\alpha }-\frac{1}{2}{V}_{\beta }$ < 0	$-\frac{\sqrt{3}}{2}{V}_{\alpha }-\frac{1}{2}{V}_{\beta }$ < 0
III	$V_{\beta }$ > 0	$\frac{V_{\beta }}{V_{\alpha }}<\sqrt{3}$	$\frac{\sqrt{3}}{2}{V}_{\alpha }-\frac{1}{2}{V}_{\beta }$ < 0	$-\frac{\sqrt{3}}{2}{V}_{\alpha }-\frac{1}{2}{V}_{\beta }$ > 0
IV	$V_{\beta }$ < 0	$\frac{V_{\beta }}{V_{\alpha }}<\sqrt{3}$	$\frac{\sqrt{3}}{2}{V}_{\alpha }-\frac{1}{2}{V}_{\beta }$ < 0	$-\frac{\sqrt{3}}{2}{V}_{\alpha }-\frac{1}{2}{V}_{\beta }$ > 0
V	$V_{\beta }$ < 0	$\frac{V_{\beta }}{|V_{\alpha }|}>\sqrt{3}$	$\frac{\sqrt{3}}{2}{V}_{\alpha }-\frac{1}{2}{V}_{\beta }$ > 0	$-\frac{\sqrt{3}}{2}{V}_{\alpha }-\frac{1}{2}{V}_{\beta }$ > 0
VI	$V_{\beta }$ < 0	$\frac{-V_{\beta }}{V_{\alpha }}<\sqrt{3}$	$\frac{\sqrt{3}}{2}{V}_{\alpha }-\frac{1}{2}{V}_{\beta }$ > 0	$-\frac{\sqrt{3}}{2}{V}_{\alpha }-\frac{1}{2}{V}_{\beta }$ < 0

如上所示:
将ABC三相在α-β 坐标系下 , 建立以$V_{\beta }$轴为参考的坐标系

新的坐标系在MATLAB中的仿真

如上所示:

• 可以观察到 , 在每一个扇区都存在 两条曲线在 其中一侧 , 一条曲线在另一侧
• 通过判断这三条曲线 与 0的关系即可确定当前所在的扇区.

---

3.4.3 小结

通过以上的计算结论 , 可以通过以下三个数值来判断扇区。
$$\{\begin{array}{l}{V}_a=V_{\beta }\\ V_b=\frac{\sqrt{3}}{2}{V}_{\alpha }-\frac{1}{2}{V}_{\beta }\\ V_c=-\frac{\sqrt{3}}{2}{V}_a-\frac{1}{2}{V}_{\beta }\end{array}$$

• 当$V_a$ > 0时, 令 A = 1; else A = 0;
• 当$V_b$ > 0时 , 令B = 1; else B = 0;
• 当$V_c$ > 0 时, 令C = 1; else C = 0;
• 且 N = 4C + 2B + A ,
• 通过N , 与各个扇区进行唯一的对应 , 且对ABC 三相利用一个二进制数字进行表示

扇区	$-\frac{\sqrt{3}}{2}{V}_a-\frac{1}{2}{V}_{\beta }$ ( C)	\ $\frac{\sqrt{3}}{2}{V}_{\alpha }-\frac{1}{2}{V}_{\beta }$ (B)	$V_{\beta }$ (A)	N=4C+2B+A
I	0	1	1	3
II	0	0	1	1
III	1	0	1	5
IV	1	0	0	4
V	1	1	0	6
VI	0	1	0	2

---

3.5 电压利用率

结论放前面: SVPWM的电压利用率是100%

3.5.1 公式与结论

首先电压利用率的公式:
$$直流母线电压利用率=\frac{输出线电压幅值}{直流母线电压}\text{\hspace{1em}(公式1)}$$
前面提到ABC三相电压空间矢量
$$\{\begin{array}{l}{U}_a=U_m\times \cos \theta \\ U_b=U_m\times \cos (\theta -\frac{2}{3}\pi )\\ U_b=U_m\times \cos (\theta +\frac{2}{3}\pi )\end{array}$$

三相电压合成的空间矢量(即输出电压)
$$U=U_a+U_b\cdot e^{j\frac{2\pi }{3}}+U_c\cdot e^{-j\frac{2\pi }{3}}=\frac{3}{2}{U}_m\cdot e^{j\theta }\text{\hspace{1em}(结论1)}$$

小结：

• 可以看到 , $U$ 是一个幅值为相电压峰值1.5倍的旋转空间矢量
• 且空间矢量$U$在三相坐标轴 (a , b , c)上投影是对称的三相正弦量

合成空间矢量$U$的推导过程 (记住结论就行 , 过程随便看看)

---

3.5.2 小结

• 三相正弦电压合成的空间矢量的幅值是相电压幅值的 $\frac{3}{2}$倍

• 三相的相电压幅值最高为$\frac{2U_{dc}}{3}$ (怎么来的可以看前面提到的这个表格)

• 所以合成矢量电压幅值 $U=\frac{2U_{dc}}{3}\times \frac{3}{2}=U_{dc}$

• 代入**(公式1)**得 , $直流母线电压利用率=\frac{U_{dc}}{U_{dc}}=100\%$

  
  

---

3.6 矢量作用时间计算

3.6.1 第一扇区

• 已知条件

$$\{\begin{array}{l}\left|U_4\right|=\left|U_6\right|=\frac{2}{3}\left|U_{dc}\right|\\ \\ U_{ref}\cdot T_s=U_4\cdot T_4+U_6\cdot T_6+U_0\cdot T_0\\ \\ U_{ref}\times \cos \theta =U_{\alpha }\\ \\ U_{ref}\times \sin \theta =U_{\beta }\end{array}$$

• 将目标矢量$U_{ref}$ 投影到相邻两个矢量$U_4和U_6$上

$$\{\begin{array}{l}{U}_{ref}\times \cos \theta =\left|U_4\right|\times \frac{T_4}{T_s}+\left|U_6\right|\times \frac{T_6}{T_s}\times \cos \frac{\pi }{3}\\ \\ U_{ref}\times \sin \theta =\left|U_6\right|\times \frac{T_6}{T_s}\times \sin \frac{\pi }{3}\end{array}$$

• 代入已知条件得

$$\{\begin{array}{l}{U}_{\alpha }\cdot T_s=\frac{2}{3}\cdot U_{dc}(T_4+T_6\cdot \frac{1}{2})\\ \\ U_{\beta }\cdot T_s=\frac{2}{3}\cdot U_{dc}\cdot T_6\cdot \frac{\sqrt{3}}{2}\end{array}$$

• 整理解得

$$\{\begin{array}{l}{T}_6=\frac{\sqrt{3}\cdot T_s}{U_{dc}}\cdot U_{\beta }\\ \\ T_4=\frac{\sqrt{3}\cdot T_s}{U_{dc}}(\frac{\sqrt{3}}{2}{U}_{\alpha }-\frac{1}{2}{U}_{\beta })\\ \\ T_0=T_s-T_6-T_4\end{array}$$

---

3.6.2 第二扇区

注意此时的角度定义

• 将目标矢量$U_{ref}$ 投影到相邻两个矢量$U_6 $ 和 $U_2$上

$$\{\begin{array}{l}{U}_{ref}\times \cos (\theta -\frac{\pi }{3})=\left|U_6\right|\times \frac{T_6}{T_s}+\left|U_2\right|\times \frac{T_2}{T_s}\times \cos \frac{\pi }{3}\\ \\ U_{ref}\times \sin (\theta -\frac{\pi }{3})=|U_2|\times \frac{T_2}{T_s}\times \sin \frac{\pi }{3}\end{array}$$

• 最终整理解得

$$\{\begin{array}{l}{T}_2=\frac{\sqrt{3}\cdot T_s}{U_{dc}}\cdot (-\frac{\sqrt{3}}{2}{U}_{\alpha }+\frac{1}{2}{U}_{\beta })\\ \\ T_6=\frac{\sqrt{3}\cdot T_s}{U_{dc}}(\frac{\sqrt{3}}{2}{U}_{\alpha }+\frac{1}{2}{U}_{\beta })\\ \\ T_0=T_s-T_2-T_6\end{array}$$

---

3.6.3 第三到第六扇区

计算方法与上面都是一样的, 直接给出最终结果

• 第三扇区

$$\{\begin{array}{l}{T}_3=-\frac{\sqrt{3}\cdot T_s}{U_{dc}}\cdot (\frac{\sqrt{3}}{2}{U}_{\alpha }+\frac{1}{2}{U}_{\beta })\\ \\ T_2=\frac{\sqrt{3}\cdot T_s}{U_{dc}}\cdot U_{\beta }\\ \\ T_0=T_s-T_2-T_3\end{array}$$

• 第四扇区

$$\{\begin{array}{l}{T}_1=-\frac{\sqrt{3}\cdot T_s}{U_{dc}}\cdot U_{\beta }\\ \\ T_3=\frac{\sqrt{3}\cdot T_s}{U_{dc}}\cdot (-\frac{\sqrt{3}}{2}{U}_{\alpha }+\frac{1}{2}{U}_{\beta })\\ \\ T_0=T_s-T_1-T_3\end{array}$$

• 第五扇区

$$\{\begin{array}{l}{T}_5=-\frac{\sqrt{3}\cdot T_s}{U_{dc}}\cdot (-\frac{\sqrt{3}}{2}{U}_{\alpha }+\frac{1}{2}{U}_{\beta })\\ \\ T_1=-\frac{\sqrt{3}\cdot T_s}{U_{dc}}\cdot (\frac{\sqrt{3}}{2}{U}_{\alpha }+\frac{1}{2}{U}_{\beta })\\ \\ T_0=T_s-T_1-T_5\end{array}$$

• 第六扇区

$$\{\begin{array}{l}{T}_4=\frac{\sqrt{3}\cdot T_s}{U_{dc}}\cdot (\frac{\sqrt{3}}{2}{U}_{\alpha }+\frac{1}{2}{U}_{\beta })\\ \\ T_5=-\frac{\sqrt{3}\cdot T_s}{U_{dc}}\cdot U_{\beta }\\ \\ T_0=T_s-T_4-T_5\end{array}$$

---

3.6.4 小结

设每个扇区中先作用的矢量为Tx , 后作用的矢量为Ty

扇区	N	$T_x$	$T_y$
I	N = 3	$T_4=\frac{\sqrt{3}\cdot T_s}{U_{dc}}(\frac{\sqrt{3}}{2}{U}_{\alpha }-\frac{1}{2}{U}_{\beta })$	$T_6=\frac{\sqrt{3}\cdot T_s}{U_{dc}}\cdot U_{\beta }$
II	N = 1	$T_2=\frac{\sqrt{3}\cdot T_s}{U_{dc}}\cdot (-\frac{\sqrt{3}}{2}{U}_{\alpha }+\frac{1}{2}{U}_{\beta })$	$T_6=\frac{\sqrt{3}\cdot T_s}{U_{dc}}(\frac{\sqrt{3}}{2}{U}_{\alpha }+\frac{1}{2}{U}_{\beta })$
III	N = 5	$T_2=\frac{\sqrt{3}\cdot T_s}{U_{dc}}\cdot U_{\beta }$	$T_3=-\frac{\sqrt{3}\cdot T_s}{U_{dc}}\cdot (\frac{\sqrt{3}}{2}{U}_{\alpha }+\frac{1}{2}{U}_{\beta })$
IV	N = 4	$T_1=-\frac{\sqrt{3}\cdot T_s}{U_{dc}}\cdot U_{\beta }$	$T_3=\frac{\sqrt{3}\cdot T_s}{U_{dc}}\cdot (-\frac{\sqrt{3}}{2}{U}_{\alpha }+\frac{1}{2}{U}_{\beta })$
V	N = 6	$T_1=-\frac{\sqrt{3}\cdot T_s}{U_{dc}}\cdot (\frac{\sqrt{3}}{2}{U}_{\alpha }+\frac{1}{2}{U}_{\beta })$	$T_5=-\frac{\sqrt{3}\cdot T_s}{U_{dc}}\cdot (-\frac{\sqrt{3}}{2}{U}_{\alpha }+\frac{1}{2}{U}_{\beta })$
VI	N = 2	$T_4=\frac{\sqrt{3}\cdot T_s}{U_{dc}}\cdot (\frac{\sqrt{3}}{2}{U}_{\alpha }+\frac{1}{2}{U}_{\beta })$	$T_5=-\frac{\sqrt{3}\cdot T_s}{U_{dc}}\cdot U_{\beta }$

$$T_4=\frac{\sqrt{3}\cdot T_s}{U_{dc}}(\frac{\sqrt{3}}{2}{U}_{\alpha }-\frac{1}{2}{U}_{\beta })$$

补充：

• 可以看到 , 整理出来的作用时间的表达式 与 之前扇区判断中三相电压表达式类似

• 可以进一步整理 , 方便后续与代码中的部分对应起来

• 假设$K=\frac{\sqrt{3}\cdot T_s}{U_{dc}}$
  $$\{\begin{array}{l}{U}_a=U_{\beta }\\ U_b=\frac{\sqrt{3}}{2}{U}_{\alpha }-\frac{1}{2}{U}_{\beta }\\ U_c=-\frac{\sqrt{3}}{2}{U}_a-\frac{1}{2}{U}_{\beta }\\ K=\frac{\sqrt{3}\cdot T_s}{U_{dc}}\end{array}$$

进一步整理出下表

扇区	$T_0$	$T_1$	$T_2$	$T_3$	$T_4$	$T_5$	$T_6$	$T_7$
I	$(T_s-T_4-T_6)/2$	0	0	0	$K\cdot U_b$	0	$K\cdot U_a$	$(T_s-T_4-T_6)/2$
II	$(T_s-T_2-T_6)/2$	0	$-K\cdot U_b$	0	0	0	$-K\cdot U_c$	$(T_s-T_2-T_6)/2$
III	$(T_s-T_2-T_3)/2$	0	$K\cdot U_a$	$K\cdot U_c$	0	0	0	$(T_s-T_2-T_3)/2$
IV	$(T_s-T_1-T_3)/2$	$-K\cdot U_a$	0	$-K\cdot U_b$	0	0	0	$(T_s-T_1-T_3)/2$
V	$(T_s-T_1-T_5)/2$	$K\cdot U_c$	0	0	0	$K\cdot U_b$	0	$(T_s-T_1-T_5)/2$
VI	$(T_s-T_4-T_5)/2$	0	0	0	$-K\cdot U_c$	$-K\cdot U_a$	0	$(T_s-T_4-T_5)/2$

---

3.7 七段式SVPWM

3.7.1矢量作用顺序

• 我们都知道一个任意方向和大小的矢量需要8个矢量的作用时长
• 为了确保每次在一个开关周期内, 只改变一个桥臂的开关 , 需要确定每个扇区内的矢量作用顺序
• 即矢量从起点到终点的路线 , 这里选用的是七段式的SVPWM

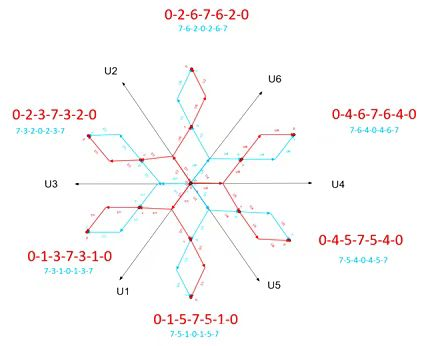
以第一扇区为例：

• 可以看到可以从$U_4$的方向开始***(0-4-6-7-6-4-0), 也可以从 $U_6$的方向开始 (7-6-4-0-4-6-7)***
• 两种方式唯一的不同就是零向量的插入方式不同

注意： 不能直接先走完其中一个再走另一个 , 那样谐波比较大

同样的方法可以得到其他扇区矢量作用顺序

---

3.7.2 矢量切换时间

• 在知道了矢量的作用顺序之后 , 就可以把矢量的作用时间换成桥臂的开关时间
• 即可以确定A、B、C三相桥臂的切换时间点

3.7.2.1 第一扇区

还是以第一扇区为例：

简单计算确定，七段SVPWM每段的作用时长 ;

(0-4-6-7-6-4-0)矢量持续时间如下图所示

• 其中$S_a$、$S_b$、$S_c$ 分别是三相桥臂的开关状态
• 各段的作用时间分别是($\frac{T_s-T_4-T_6}{4}、\frac{T_4}{2}、\frac{T_6}{2}、\frac{T_s-T_4-T_6}{2}、\frac{T_6}{2}、\frac{T_4}{2}、\frac{T_s-T_4-T_6}{4}$)

由上图可以看出, 三相桥臂的切换时间(送入定时器的比较值)
$$\{\begin{array}{l}{S}_a切换时间=\frac{T_s-T_4-T_6}{4}\\ \\ S_b切换时间=\frac{T_s-T_4-T_6}{4}+\frac{T_4}{2}=\frac{T_s+T_4-T_6}{4}\\ \\ S_c切换时间=\frac{T_s-T_4-T_6}{4}+\frac{T_4}{2}+\frac{T_6}{2}=\frac{T_s+T_4+T_6}{4}\end{array}$$

---

3.7.2.2 第二扇区

桥臂切换时间
$$\{\begin{array}{l}{S}_a切换时间=\frac{T_s+T_2-T_6}{4}\\ \\ S_b切换时间=\frac{T_s-T_2-T_6}{4}\\ \\ S_c切换时间=\frac{T_s+T_2+T_6}{4}\end{array}$$

---

3.7.2.3 第三扇区

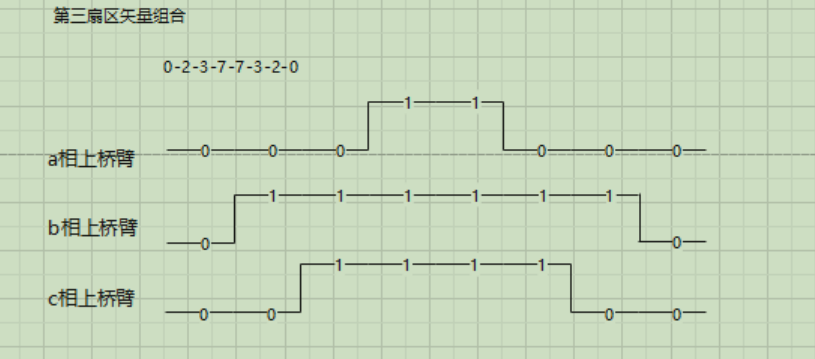
桥臂切换时间
$$\{\begin{array}{l}{S}_a切换时间=\frac{T_s+T_2+T_3}{4}\\ \\ S_b切换时间=\frac{T_s-T_2-T_3}{4}\\ \\ S_c切换时间=\frac{T_s+T_2-T_3}{4}\end{array}$$

---

3.7.2.4 第四扇区

桥臂切换时间
$$\{\begin{array}{l}{S}_a切换时间=\frac{T_s+T_1+T_3}{4}\\ \\ S_b切换时间=\frac{T_s+T_1-T_3}{4}\\ \\ S_c切换时间=\frac{T_s-T_1-T_3}{4}\end{array}$$

---

3.7.2.5 第五扇区

(0-1-5-7-7-5-1-0)

桥臂切换时间
$$\{\begin{array}{l}{S}_a切换时间=\frac{T_s+T_1-T_5}{4}\\ \\ S_b切换时间=\frac{T_s+T_1+T_5}{4}\\ \\ S_c切换时间=\frac{T_s-T_1-T_5}{4}\end{array}$$

---

3.7.2.6 第六扇区

(0-4-5-7–7-5-4-0)

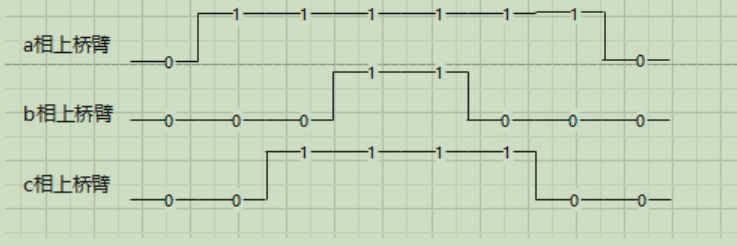
桥臂切换时间
$$\{\begin{array}{l}{S}_a切换时间=\frac{T_s-T_4-T_5}{4}\\ \\ S_b切换时间=\frac{T_s+T_4+T_5}{4}\\ \\ S_c切换时间=\frac{T_s+T_4-T_5}{4}\end{array}$$

---

3.8 MATLAB仿真

3.8.1 svpwm模块与函数代码

3.8.1.1 仿真框图

如图所示：

• 输入$V_d和V_q$的期望以及角度信息
• 经过反park变换 和 svpwm运算模块后 输出三相桥臂的切换时间

3.8.1.2代码实现

将前面扇区判断, 矢量作用时长计算的公式结果写入代码即可

%输入输出
function [T_Sa,T_Sb,T_Sc,sector] = fsvpwm(V_alpha,V_beta,Udc,Tpwm)

%输出全部转换为单精度浮点型
sector = single(0);         %扇区N值
T_Sa = single(0);           %桥臂切换时间
T_Sb = single(0);           %桥臂切换时间
T_Sc = single(0);           %桥臂切换时间


%========中间变量(用于判断扇区与矢量作用时间)================
    
    %用于判断扇区
    Vref1 = V_beta;							          %A         
    Vref2 = (sqrt(3)*V_alpha - V_beta)/2;             %B	    
    Vref3 = (-sqrt(3)*V_alpha - V_beta)/2;            %C
    
    
    %用于计算矢量作用时长
    K = sqrt(3)*Tpwm/Udc;   
    
    X = K*Vref1;                
    Y = K*Vref2;
    Z = K*Vref3;
    
%==========扇区判断================

% N = 4C + 2B + A
  if (Vref1>0)
	   sector = single(1);
  end
  if (Vref2>0)
	   sector = sector+single(2);
  end
  if (Vref3>0)
       sector = sector+single(4);
  end

  
%======== 矢量作用时间计算 ===================

% 设每个扇区中先作用的矢量为Tx , 后作用的矢量为Ty
switch (sector)   
    case 1
        Tx = -Y; Ty = -Z;           %第二扇区
	case 2
        Tx = -Z; Ty = -X;           %第六扇区
	case 3
        Tx = Y; Ty = X;             %第一扇区
	case 4
        Tx = -X; Ty = -Y;           %第四扇区
	case 5  
        Tx = X; Ty = Z;             %第三扇区
    otherwise
        Tx = Z; Ty = Y;             %第五扇区
end


%防止过调制,采用比例缩小的方法 (确保Tx + Ty 不超过Tpwm)
if Tx+Ty > Tpwm        
    Tx = Tx*Tpwm/(Tx+Ty);
    Ty = Ty*Tpwm/(Tx+Ty);
else
    Tx = Tx;
    Ty = Ty;
end


%==========桥臂切换时间计算================

ta = (Tpwm-(Tx+Ty))/4.0;
tb = ta+Tx/2;
tc = tb+Ty/2;

switch (sector)
    case 1                  %第二扇区
        T_Sa=tb;
        T_Sb=ta;
        T_Sc=tc; 
        
    case 2                  %第六扇区
        T_Sa=ta;
        T_Sb=tc;
        T_Sc=tb; 
       
    case 3                  %第一扇区
        T_Sa=ta;
        T_Sb=tb;
        T_Sc=tc; 
        
    case 4                  %第四扇区
        T_Sa=tc;
        T_Sb=tb;
        T_Sc=ta;
        
    case 5                  %第三扇区
        T_Sa=tc;
        T_Sb=ta;
        T_Sc=tb;
        
   case 6                   %第五扇区
       T_Sa=tb;
       T_Sb=tc;
       T_Sc=ta;
 end
end

    

---

3.8.1.3 仿真结果

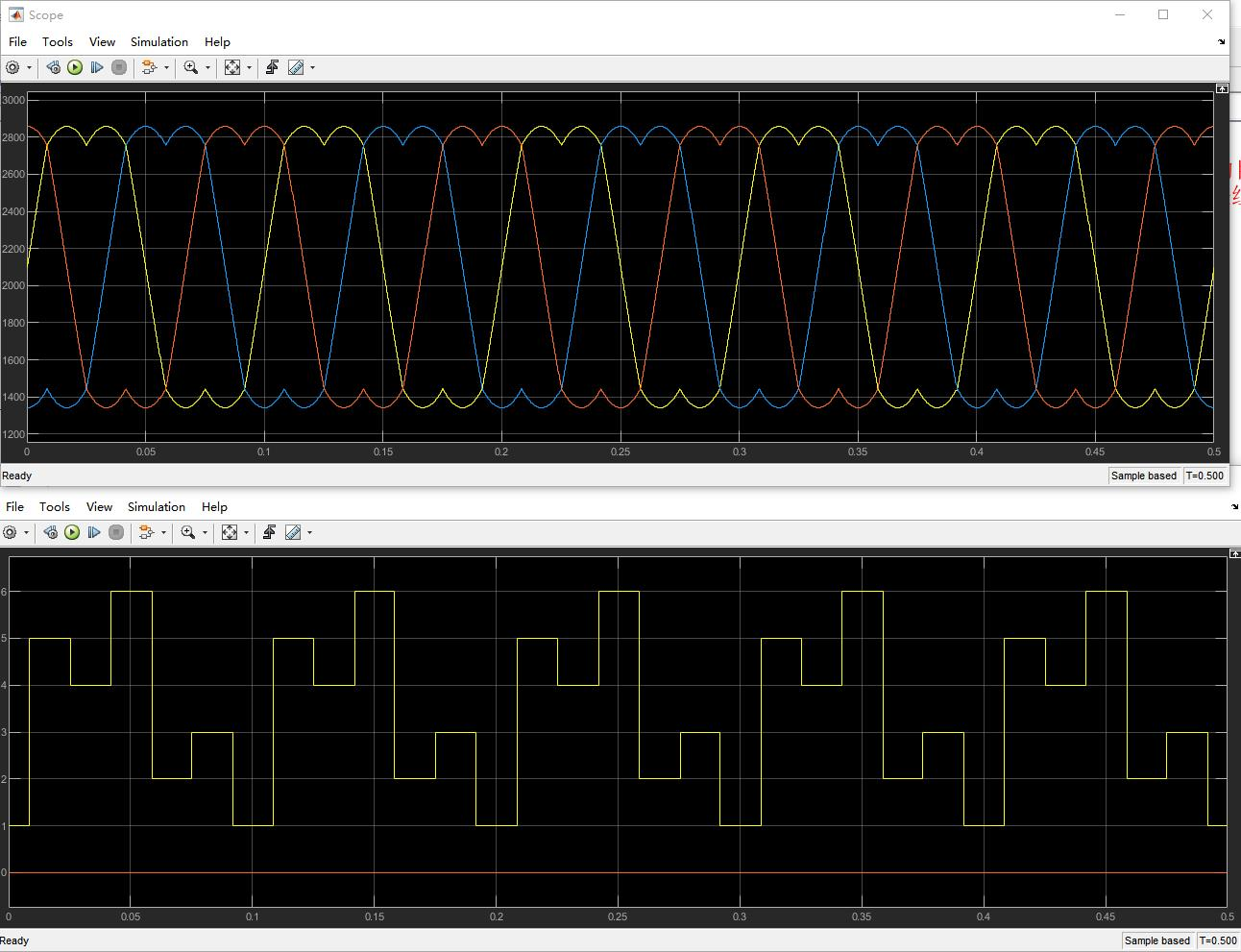
调制波形与扇区波形

如图所示

• 因为内部中点电位随零序波动，SVPWM模块调制后的波形是马鞍波
• 各个扇区对应的调制波形 , 符合之前的计算结果

---

3.8.2 开环电机驱动仿真

通过之前的坐标变换和svpwm模块 , 现在已经可以实现开环驱动电机转动

3.8.2.1 仿真框图

控制流程

• 输入期望值$U_d和U_q$ , 通过svpwm模块进行调制 , 输出三相桥臂切换时间
• 输入模拟的定时器, 输出三相互补的六路pwm
• 送入全桥, 驱动电机

控制框图

模拟定时器输出方波

---

3.8.2.2 仿真结果

三相电流波形与速度角度波形

• 三相定子电流呈现较好的正弦特性
• 在到达给定转速后, 转速稳定

三相互补六路pwm波形

---

3.9 硬件平台

---