系列文章目录
文章目录
前言
课程:台大林沛群的机器人学运动学。
书:机器人学导论。
一、导论
1.1.概述
早期目标:为了解决3D问题(dirty,dangerous,dull)
近年发展:应用变得广泛,所谓服务型机器人发展蓬勃
核心/基础:从机械手臂的学习出发,因为机械手臂的发展是最早,也是最完整的。
最大特色:与其他计算机系统相比,机器人最大的特色就是能够在在实体世界产生运动。
运动分类:操作,移动
1.2.课程情景
将一个杯子拿起来,然后将其挂在墙上
分为三步:
1)如何描述杯子的位置?(表达法:刚体在空间中的描述)
空间坐标,姿态(一个刚体在空间中转动的状态)
2)手臂的顺逆运动学
顺运动学:从驱动的角度解释:先知道手的各关节、肌肉状态,再知道手的末端点的状态。
逆运动学:从需求的角度解释:先知道手想要的特定位置和姿态,再反算手的各关节、肌肉需要的状态。(真是需求中常常时逆运动学)
3)轨迹规划
知道手末端状态和关节肌肉状态后,要移动杯子,杯子要怎么动才是比较顺的(顺:在某瞬间不会有突然的加速度跑出)
二、刚体运动状态描述
2.1.刚体状态描述
平面:移动2DOFs、转动1DOF(DOF:Degree of freedom 自由度)
空间:移动3DOFs、转动3DOFs
2.2.整合表达刚体的状态
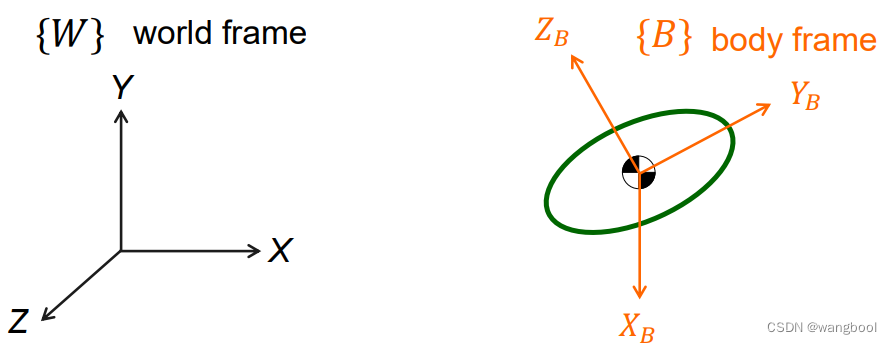
在刚体上建立frame,常建在质心上
移动:由body frame的原点状态判定
P
⃗
=
[
P
x
P
y
P
z
]
=
A
P
B
o
r
g
=
o
r
i
g
i
n
o
f
{
B
}
r
e
p
r
e
s
e
n
t
e
d
i
n
{
A
}
\vec{P} = \begin{bmatrix}P_x \\ P_y \\ P_z\end{bmatrix} = {^A}P{_B~org} = origin~of ~\{ B\}~represented~in~\{A\}
P=
PxPyPz
=APB org=origin of {B} represented in {A}
转动:由body frame的姿态判定
B
A
R
=
[
A
X
^
B
A
Y
^
B
A
Z
^
B
]
=
[
X
^
B
⋅
X
^
A
Y
^
B
⋅
X
^
A
Z
^
B
⋅
X
^
A
X
^
B
⋅
Y
^
A
Y
^
B
⋅
Y
^
A
Z
^
B
⋅
Y
^
A
X
^
B
⋅
Z
^
A
Y
^
B
⋅
Z
^
A
Z
^
B
⋅
Z
^
A
]
=
B
r
e
l
a
t
i
v
e
t
o
A
{^A_B}R = \begin{bmatrix}&&\\ {^A}\widehat X{_B} &{^A}\widehat Y{_B}& {^A}\widehat Z{_B}\\&&\end{bmatrix}= \begin{bmatrix}{\widehat X_B}\cdot{\widehat X_A}&{\widehat Y_B}\cdot{\widehat X_A}&{\widehat Z_B}\cdot{\widehat X_A}\\{\widehat X_B}\cdot{\widehat Y_A}&{\widehat Y_B}\cdot{\widehat Y_A}&{\widehat Z_B}\cdot{\widehat Y_A}\\{\widehat X_B}\cdot{\widehat Z_A}&{\widehat Y_B}\cdot{\widehat Z_A}&{\widehat Z_B}\cdot{\widehat Z_A}\end{bmatrix}=B ~relative~to~A
BAR=
AX
BAY
BAZ
B
=
X
B⋅X
AX
B⋅Y
AX
B⋅Z
AY
B⋅X
AY
B⋅Y
AY
B⋅Z
AZ
B⋅X
AZ
B⋅Y
AZ
B⋅Z
A
=B relative to A
整合后:
B
=
{
B
A
R
,
A
P
B
o
r
g
}
{B}=\{ {^A_B}R~,{^A}P{_B~org}\}
B={BAR ,APB org},只能表达,无法定量计算
2.3.刚体的运动状态描述
移动:将质心运动位置轨迹记录下来,用轨迹对时间的微分,得到质心速度的状态,再一次微分得到加速度的状态
转动:也是通过一次微分和二次微分获得角速度和角加速度

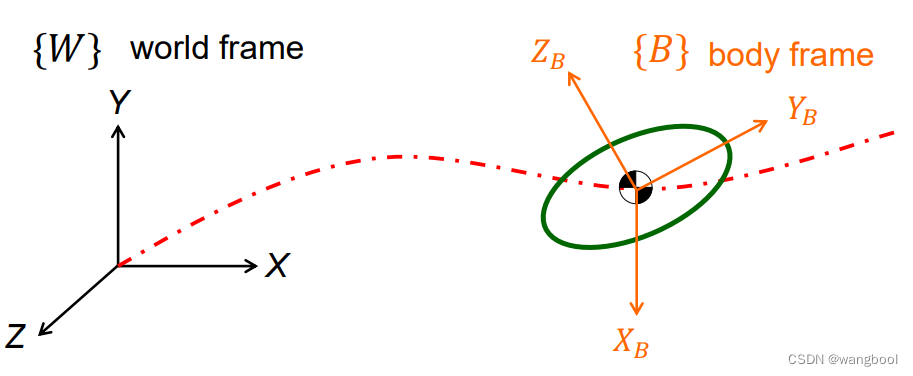
2.4.移动
以向量(vector)
P
⃗
\vec {P}
P来描述{B}的原点相对于{A}的状态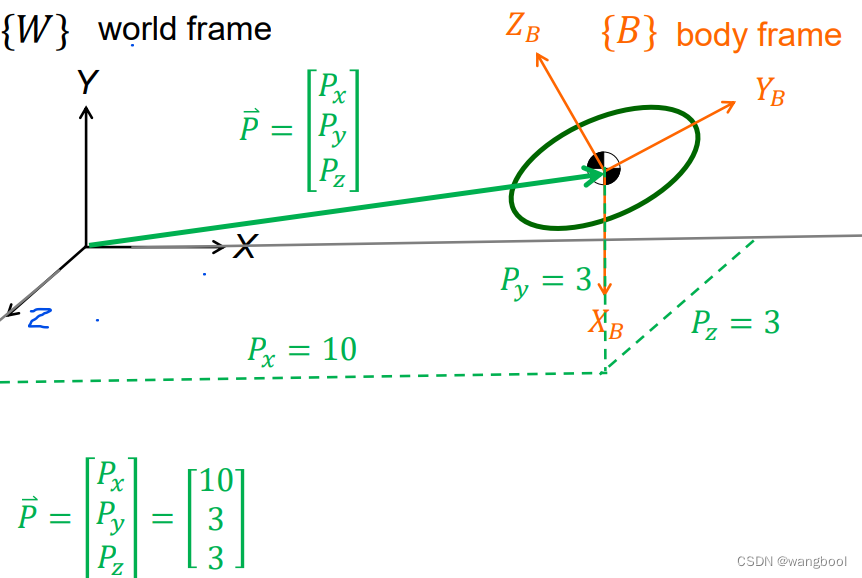
2.5.向量可表达空间关系的两个方式
1)A position in space(i.e.,positon vector)
以此方式描述在world frame下的body frame原点
P
⃗
=
[
P
x
P
y
P
z
]
=
A
P
B
o
r
g
=
o
r
i
g
i
n
o
f
{
B
}
r
e
p
r
e
s
e
n
t
e
d
i
n
{
A
}
\vec{P} = \begin{bmatrix}P_x \\ P_y \\ P_z\end{bmatrix} = {^A}P{_B~org} = origin~of ~\{ B\}~represented~in~\{A\}
P=
PxPyPz
=APB org=origin of {B} represented in {A}
2)A vector(i.e.,displacement,frame basis)
以此方式表达bady frame上principal axes的方向

三、转动(转动矩阵)
3.1.定义(表示{B}相对于{A}的姿态)
B
A
R
=
[
X
^
B
⋅
X
^
A
Y
^
B
⋅
X
^
A
Z
^
B
⋅
X
^
A
X
^
B
⋅
Y
^
A
Y
^
B
⋅
Y
^
A
Z
^
B
⋅
Y
^
A
X
^
B
⋅
Z
^
A
Y
^
B
⋅
Z
^
A
Z
^
B
⋅
Z
^
A
]
=
B
r
e
l
a
t
i
v
e
t
o
A
{^A_B}R = \begin{bmatrix}{\widehat X_B}\cdot{\widehat X_A}&{\widehat Y_B}\cdot{\widehat X_A}&{\widehat Z_B}\cdot{\widehat X_A}\\{\widehat X_B}\cdot{\widehat Y_A}&{\widehat Y_B}\cdot{\widehat Y_A}&{\widehat Z_B}\cdot{\widehat Y_A}\\{\widehat X_B}\cdot{\widehat Z_A}&{\widehat Y_B}\cdot{\widehat Z_A}&{\widehat Z_B}\cdot{\widehat Z_A}\end{bmatrix}=B ~relative~to~A
BAR=
X
B⋅X
AX
B⋅Y
AX
B⋅Z
AY
B⋅X
AY
B⋅Y
AY
B⋅Z
AZ
B⋅X
AZ
B⋅Y
AZ
B⋅Z
A
=B relative to A
Rotation Matrix的三个columns即为frame{B}的basis:
X
B
,
Y
B
,
Z
B
X_B,Y_B,Z_B
XB,YB,ZB在{A}上的表示
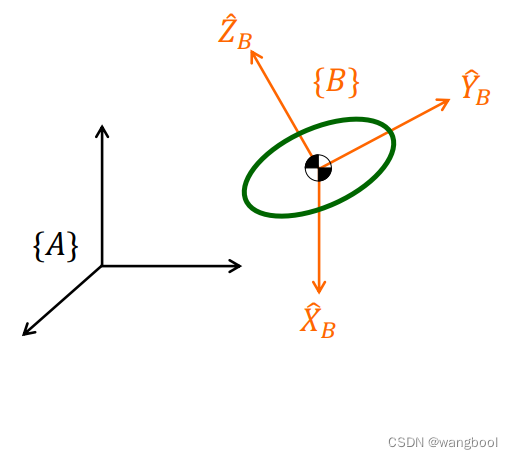
Ex:{B}相对于{A}的姿态
B
A
R
=
{^A_B}R=
BAR=?
例题一:
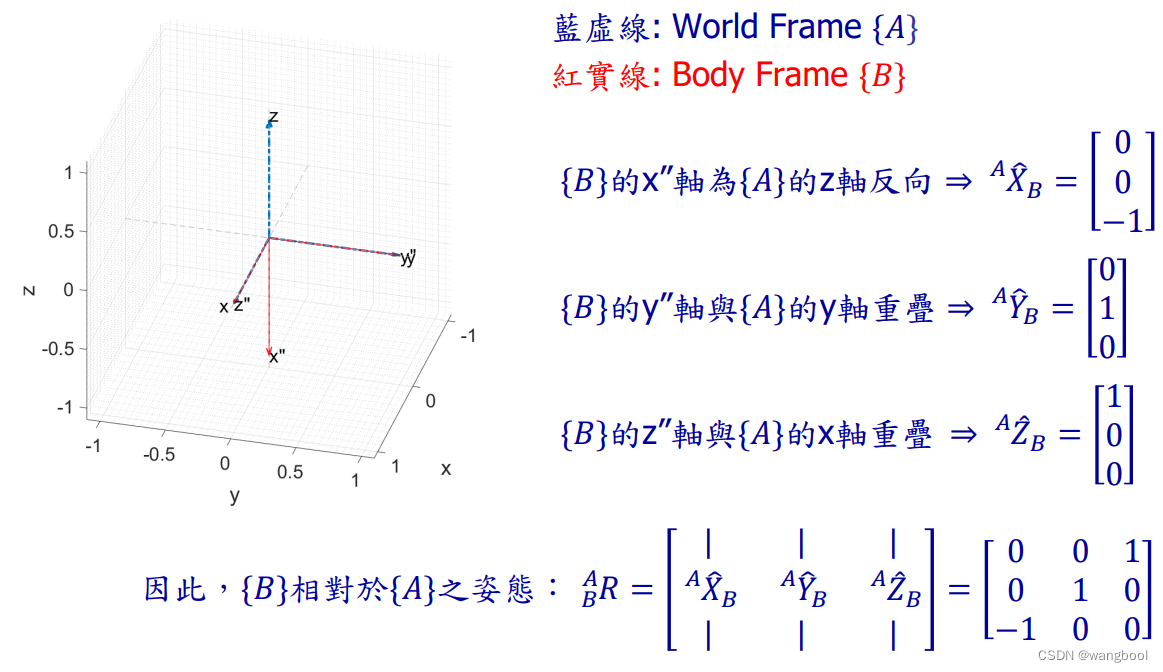
例题二:
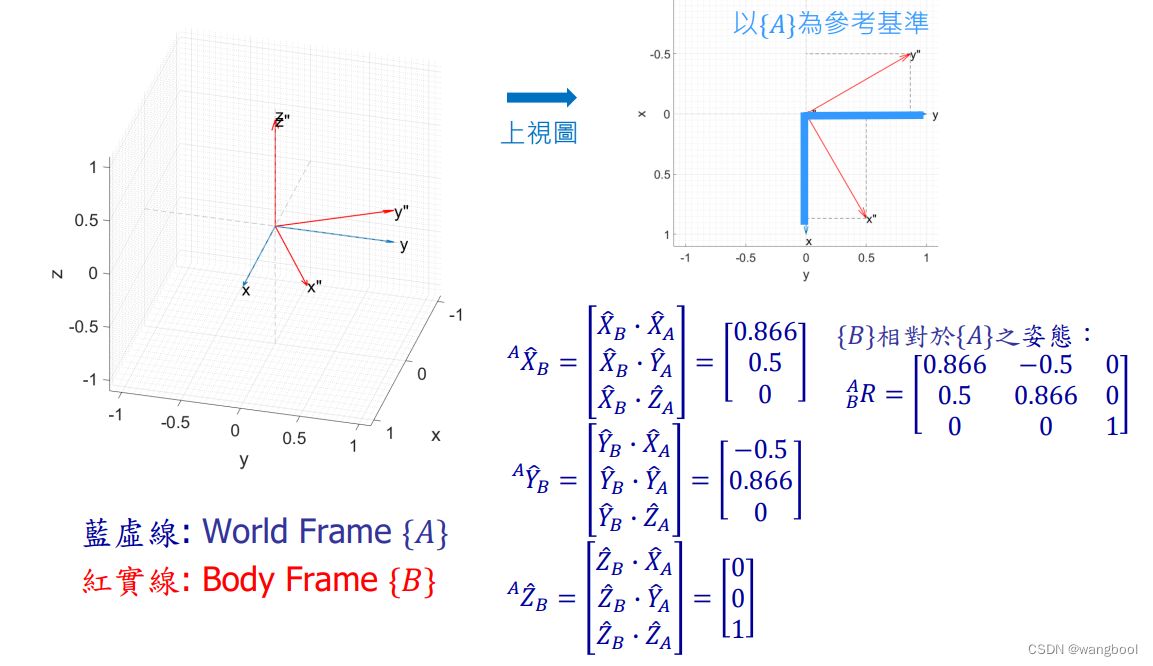
练习:
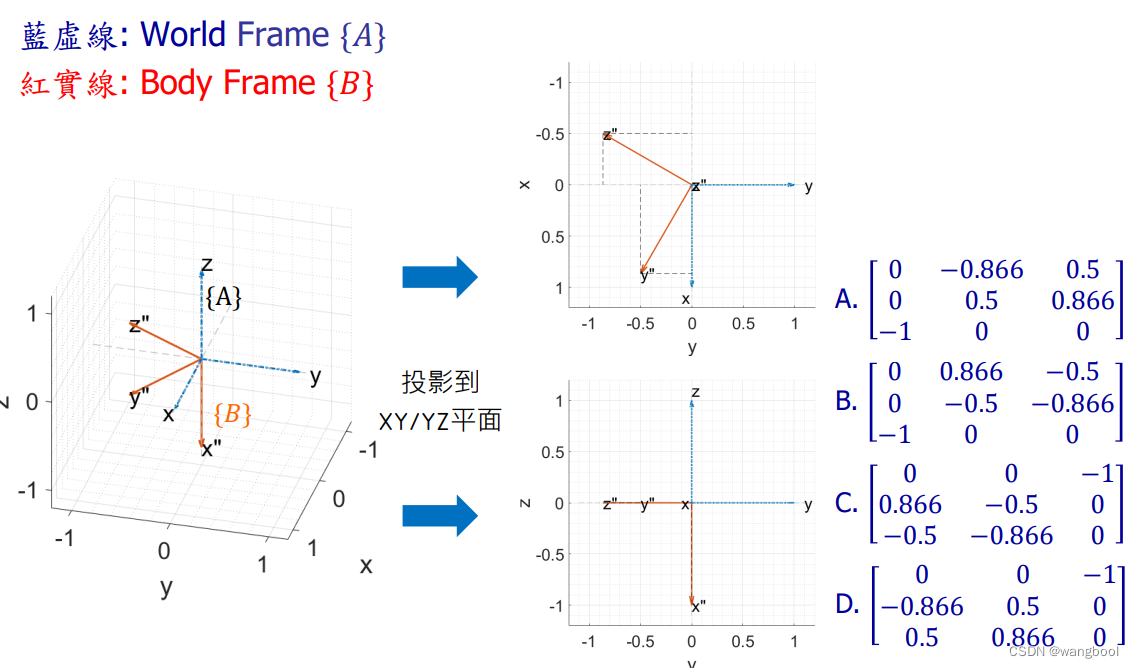
3.2.Rotation Matrix的特性
1)表达{B}相对于{A}的姿态的rotation matrix的转置即为表达{A}相对于{B}的姿态的rotation matrix。
过程如下:
B
A
R
=
[
X
^
B
⋅
X
^
A
Y
^
B
⋅
X
^
A
Z
^
B
⋅
X
^
A
X
^
B
⋅
Y
^
A
Y
^
B
⋅
Y
^
A
Z
^
B
⋅
Y
^
A
X
^
B
⋅
Z
^
A
Y
^
B
⋅
Z
^
A
Z
^
B
⋅
Z
^
A
]
=
[
A
X
^
B
A
Y
^
B
A
Z
^
B
]
{^A_B}R = \begin{bmatrix}{\widehat X_B}\cdot{\widehat X_A}&{\widehat Y_B}\cdot{\widehat X_A}&{\widehat Z_B}\cdot{\widehat X_A}\\{\widehat X_B}\cdot{\widehat Y_A}&{\widehat Y_B}\cdot{\widehat Y_A}&{\widehat Z_B}\cdot{\widehat Y_A}\\{\widehat X_B}\cdot{\widehat Z_A}&{\widehat Y_B}\cdot{\widehat Z_A}&{\widehat Z_B}\cdot{\widehat Z_A}\end{bmatrix}= \begin{bmatrix}&&\\ {^A}\widehat X{_B} &{^A}\widehat Y{_B}& {^A}\widehat Z{_B}\\&&\end{bmatrix}
BAR=
X
B⋅X
AX
B⋅Y
AX
B⋅Z
AY
B⋅X
AY
B⋅Y
AY
B⋅Z
AZ
B⋅X
AZ
B⋅Y
AZ
B⋅Z
A
=
AX
BAY
BAZ
B
内积前后项交换不变,因此前后向量互换后有
B
A
R
=
[
X
^
A
⋅
X
^
B
X
^
A
⋅
Y
^
B
X
^
A
⋅
Z
^
B
Y
^
A
⋅
X
^
B
Y
^
A
⋅
Y
^
B
Y
^
A
⋅
Z
^
B
Z
^
A
⋅
X
^
B
Z
^
A
⋅
Y
^
B
Z
^
A
⋅
Z
^
B
]
=
[
B
X
^
A
T
B
Y
^
A
T
B
Z
^
A
T
]
=
[
B
X
^
A
B
Y
^
A
B
Z
^
A
]
T
=
A
B
R
T
{^A_B}R=\begin{bmatrix}{\widehat X_A}\cdot{\widehat X_B}&{\widehat X_A}\cdot{\widehat Y_B}&{\widehat X_A}\cdot{\widehat Z_B}\\{\widehat Y_A}\cdot{\widehat X_B}&{\widehat Y_A}\cdot{\widehat Y_B}&{\widehat Y_A}\cdot{\widehat Z_B}\\{\widehat Z_A}\cdot{\widehat X_B}&{\widehat Z_A}\cdot{\widehat Y_B}&{\widehat Z_A}\cdot{\widehat Z_B}\end{bmatrix}=\begin{bmatrix}&{^B}\widehat X{_A}^T &\\ &{^B}\widehat Y{_A}^T&\\& {^B}\widehat Z{_A}^T&\end{bmatrix}\\~\\ = {\begin{bmatrix}&&\\ {^B}\widehat X{_A} &{^B}\widehat Y{_A}& {^B}\widehat Z{_A}\\&&\end{bmatrix}}^T = {{^B_A}R}^T \quad\quad\quad\quad\quad\quad~~~
BAR=
X
A⋅X
BY
A⋅X
BZ
A⋅X
BX
A⋅Y
BY
A⋅Y
BZ
A⋅Y
BX
A⋅Z
BY
A⋅Z
BZ
A⋅Z
B
=
BX
ATBY
ATBZ
AT
=
BX
ABY
ABZ
A
T=ABRT
即:
B
A
R
=
A
B
R
T
{^A_B}R = {{^B_A}R}^T\quad\quad\quad\quad\quad
BAR=ABRT
Ex:{A}相对于{B}的姿态
A
B
R
=
{^B_A}R=
ABR=?
第一题:
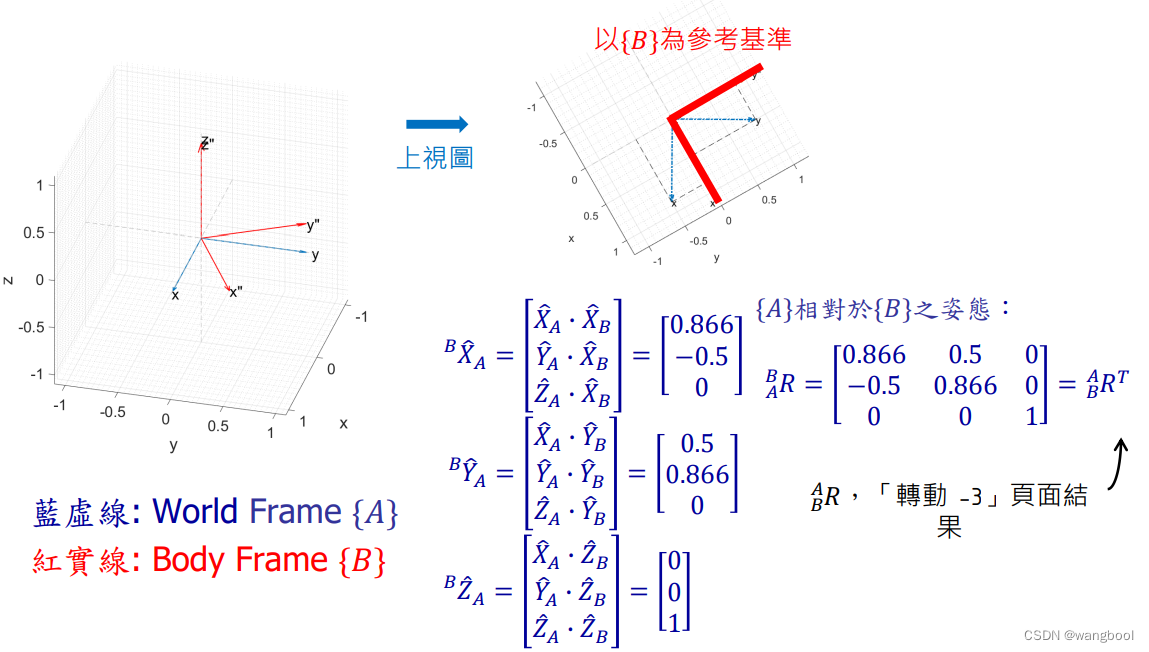
将Rotation Matrix与自己的转置相乘得到单位矩阵,过程如下:
B
A
R
T
B
A
R
=
[
B
X
^
A
B
Y
^
A
B
Z
^
A
]
T
[
A
X
^
B
A
Y
^
B
A
Z
^
B
]
=
[
B
X
^
A
T
B
Y
^
A
T
B
Z
^
A
T
]
[
A
X
^
B
A
Y
^
B
A
Z
^
B
]
=
[
1
0
0
0
1
0
0
0
1
]
=
I
3
(
3
×
3
i
d
e
n
t
i
t
y
m
a
t
r
i
x
)
=
B
A
R
−
1
B
A
R
{{^A_B}R}^T{^A_B}R= {\begin{bmatrix}&&\\ {^B}\widehat X{_A} &{^B}\widehat Y{_A}& {^B}\widehat Z{_A}\\&&\end{bmatrix}}^T\begin{bmatrix}&&\\ {^A}\widehat X{_B} &{^A}\widehat Y{_B}& {^A}\widehat Z{_B}\\&&\end{bmatrix} \\~\\ =\begin{bmatrix}&{^B}\widehat X{_A}^T &\\ &{^B}\widehat Y{_A}^T&\\& {^B}\widehat Z{_A}^T&\end{bmatrix}\begin{bmatrix}&&\\ {^A}\widehat X{_B} &{^A}\widehat Y{_B}& {^A}\widehat Z{_B}\\&&\end{bmatrix} ~\\~\\ \quad\quad=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}=I_3(3 \times3~identity~matrix)\\~\\={{^A_B}R}^{-1}{^A_B}R\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad
BARTBAR=
BX
ABY
ABZ
A
T
AX
BAY
BAZ
B
=
BX
ATBY
ATBZ
AT
AX
BAY
BAZ
B
=
100010001
=I3(3×3 identity matrix) =BAR−1BAR
即得:
B
A
R
T
=
B
A
R
−
1
=
A
B
R
{{^A_B}R}^T = {{^A_B}R}^{-1} ={^B_A}R
BART=BAR−1=ABR
因此:
2)Rotation Matrix一定是非奇异阵。
3)Rotation Matrix是正交矩阵,即Rotation Matrix的转置等于其逆阵。
4)Rotation Matrix的每一个columns都是一个orthonormal basis,并且:长度为1,columns之间互相垂直。
5)Rotation Matrix有九个数字,但是上列两个条件(长度为1,columns之间互相垂直)置入了6个constraints,所以只有3个DOFs,与空间中转动具有3DOFs相符。
6)Determinant = 1(rotation)= -1(reflection)
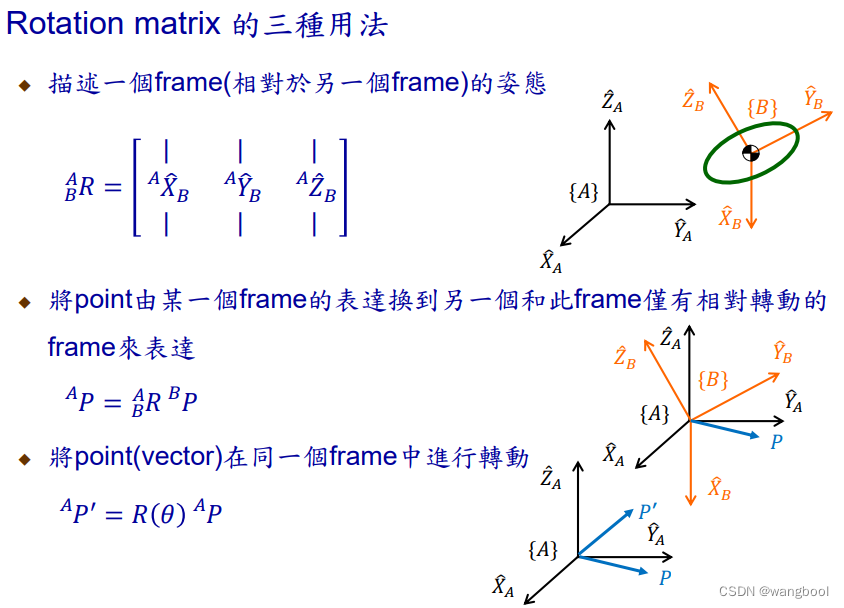
3.3.Rotation Matrix的作用
1)描述一个frame相对于另一个frame的姿态,见3.2
2)mapping:将point在某一个frame下的表达转到另一个和此frame有相对运动的frame来表达。
o
r
i
g
i
n
a
l
c
o
o
d
i
n
a
t
e
B
P
^
=
B
P
x
X
^
B
+
B
P
y
Y
^
B
+
B
P
z
Z
^
B
n
e
w
c
o
o
d
i
n
a
t
e
A
P
^
=
A
P
x
X
^
A
+
A
P
y
Y
^
A
+
A
P
z
Z
^
A
A
P
x
=
B
P
^
⋅
X
^
A
=
X
^
B
⋅
X
^
A
B
P
x
+
Y
^
B
⋅
X
^
A
B
P
y
+
Z
^
B
⋅
X
^
A
B
P
z
A
P
y
=
B
P
^
⋅
Y
^
A
=
X
^
B
⋅
Y
^
A
B
P
x
+
Y
^
B
⋅
Y
^
A
B
P
y
+
Z
^
B
⋅
Y
^
A
B
P
z
A
P
z
=
B
P
^
⋅
Z
^
A
=
X
^
B
⋅
Z
^
A
B
P
x
+
Y
^
B
⋅
Z
^
A
B
P
y
+
Z
^
B
⋅
Z
^
A
B
P
z
original~coodinate~^B\widehat P = {^BP_x}{\widehat X_B}+ {^BP_y}{\widehat Y_B}+ {^BP_z}{\widehat Z_B\quad\quad\quad\quad}\\~\\ new~coodinate~^A \widehat P = {^AP_x}{\widehat X_A}+ {^AP_y}{\widehat Y_A}+ {^AP_z}{\widehat Z_A}\quad\quad\\~\\\\ ^AP_x={^B}\widehat P\cdot \widehat X_A=\widehat X_B\cdot {\widehat X_A}{^BP_x}+ \widehat Y_B\cdot{\widehat X_A} {^BP_y}+\widehat Z_B\cdot {\widehat X_A}{^BP_z}\\~\\\\ ^AP_y={^B}\widehat P\cdot \widehat Y_A=\widehat X_B\cdot {\widehat Y_A}{^BP_x}+ \widehat Y_B\cdot{\widehat Y_A} {^BP_y}+\widehat Z_B\cdot {\widehat Y_A}{^BP_z}\\~\\\\ ^AP_z={^B}\widehat P\cdot \widehat Z_A=\widehat X_B\cdot {\widehat Z_A}{^BP_x}+ \widehat Y_B\cdot{\widehat Z_A} {^BP_y}+\widehat Z_B\cdot {\widehat Z_A}{^BP_z}\\~\\\\
original coodinate BP
=BPxX
B+BPyY
B+BPzZ
B new coodinate AP
=APxX
A+APyY
A+APzZ
A APx=BP
⋅X
A=X
B⋅X
ABPx+Y
B⋅X
ABPy+Z
B⋅X
ABPz APy=BP
⋅Y
A=X
B⋅Y
ABPx+Y
B⋅Y
ABPy+Z
B⋅Y
ABPz APz=BP
⋅Z
A=X
B⋅Z
ABPx+Y
B⋅Z
ABPy+Z
B⋅Z
ABPz
即得:
A
P
^
=
A
[
P
x
P
y
P
z
]
=
[
X
^
B
⋅
X
^
A
Y
^
B
⋅
X
^
A
Z
^
B
⋅
X
^
A
X
^
B
⋅
Y
^
A
Y
^
B
⋅
Y
^
A
Z
^
B
⋅
Y
^
A
X
^
B
⋅
Z
^
A
Y
^
B
⋅
Z
^
A
Z
^
B
⋅
Z
^
A
]
B
[
P
x
P
y
P
z
]
=
B
A
R
B
P
^
^A\widehat P=^A{\begin{bmatrix} P_x\\P_y\\P_z \end{bmatrix}}={\begin{bmatrix}{\widehat X_B}\cdot{\widehat X_A}&{\widehat Y_B}\cdot{\widehat X_A}&{\widehat Z_B}\cdot{\widehat X_A}\\{\widehat X_B}\cdot{\widehat Y_A}&{\widehat Y_B}\cdot{\widehat Y_A}&{\widehat Z_B}\cdot{\widehat Y_A}\\{\widehat X_B}\cdot{\widehat Z_A}&{\widehat Y_B}\cdot{\widehat Z_A}&{\widehat Z_B}\cdot{\widehat Z_A}\end{bmatrix}}^B{\begin{bmatrix} P_x\\P_y\\P_z \end{bmatrix}}={^A_B}R{^B\widehat P}
AP
=A
PxPyPz
=
X
B⋅X
AX
B⋅Y
AX
B⋅Z
AY
B⋅X
AY
B⋅Y
AY
B⋅Z
AZ
B⋅X
AZ
B⋅Y
AZ
B⋅Z
A
B
PxPyPz
=BARBP
在这里, B P ^ {^B\widehat P} BP 是{B}上的一个坐标矩阵, A P ^ {^A\widehat P} AP 是{A}上的一个坐标矩阵,虽然两个坐标矩阵数值不一样,实际上是在不同的frame上表示一个相同的point, B A R {^A_B}R BAR就是{B}转到{A}的过渡矩阵。
旧基表新基,矩阵是右乘;新坐标表旧坐标,矩阵是左乘。也即是说,如果是一个frame转到另一个frame,即用这个旧frame的basis右乘rotation matrix,得到要转到的frame,如果是要在一个frame上表示另一个frame上的坐标向量,则原frame的坐标向量左乘上rotation matrix。
Ex:
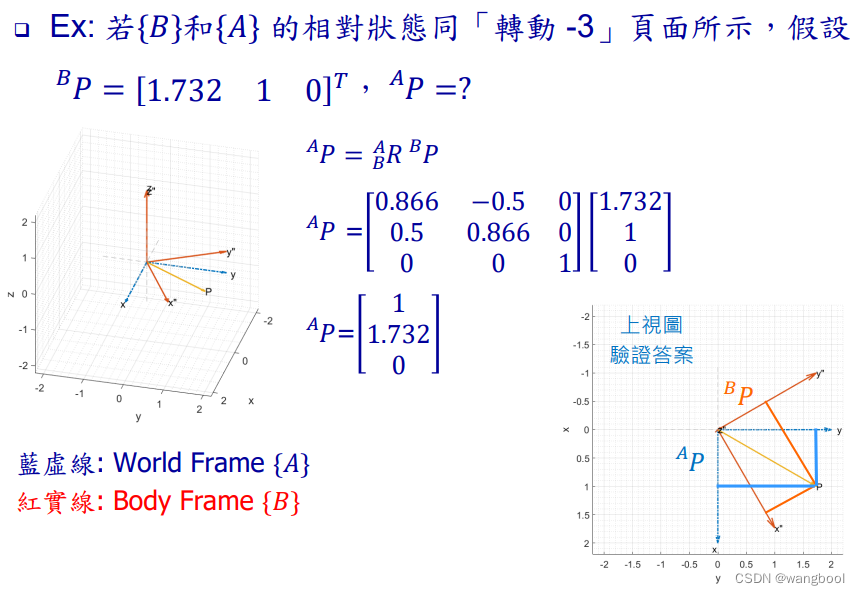
3)Operator:进一步描述物体转动的状态,将point(vector)在一个frame下的转动。
这里主要以对三个principal axes旋转的matrix为基础
About
Z
A
^
w
i
t
h
θ
\widehat {Z_A}~with~\theta
ZA
with θ
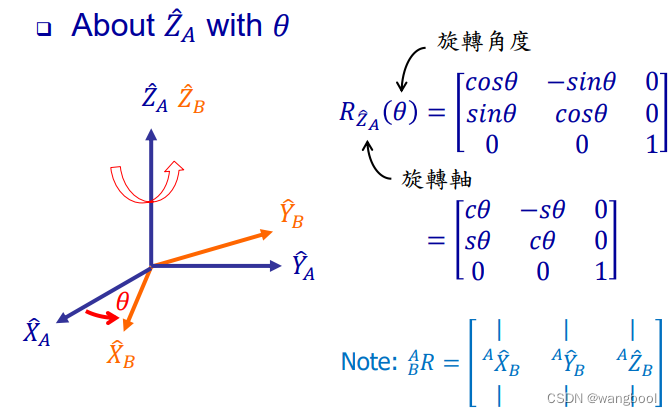
About
Z
A
^
w
i
t
h
θ
\widehat {Z_A}~with~\theta
ZA
with θ
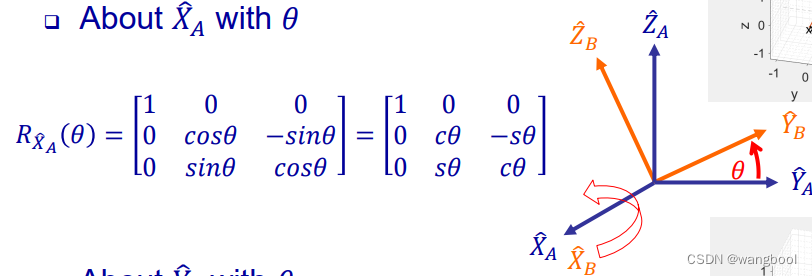
About
Y
A
^
w
i
t
h
θ
\widehat {Y_A}~with~\theta
YA
with θ
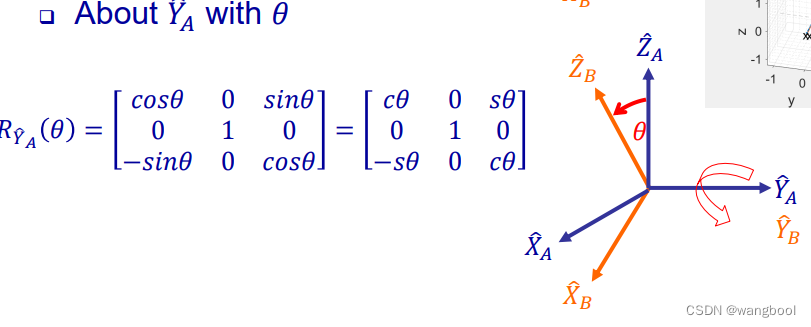
实际上就是把rotation matrix分解到了三个principal axes,绕每个principal axes各自的 θ \theta θ得到一个rotation matrix
Ex:
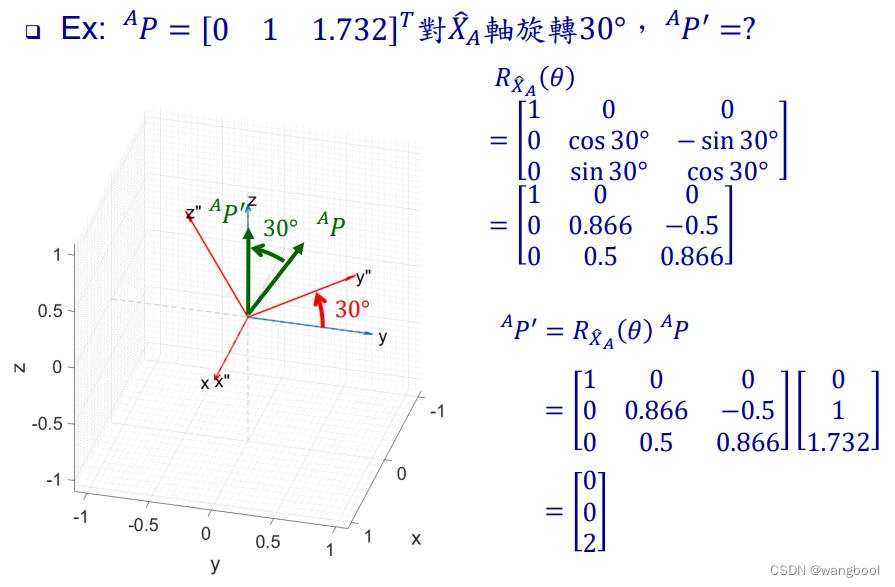
3.4总结






















 2313
2313











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








