最熟悉的陌生人| 长文理解基因本体论 (Gene Ontology, GO)

最新推荐文章于 2024-10-08 22:44:46 发布

刘永鑫Adam

最新推荐文章于 2024-10-08 22:44:46 发布

阅读量3.9k

点赞数 4

原文链接：https://mp.weixin.qq.com/s?__biz=MzUzMjA4Njc1MA==&mid=2247506182&idx=3&sn=25f5c0ea47e49380730c5381eb6216c0&chksm=faba33b7cdcdbaa13f4717b152c4b2d574d4bc7b68045487fa938d3d0b3dda4e15c3bdd22cc6&scene=126&&sessionid=0

版权

在生物信息学中，GO似乎是一个我们绕不开的话题。想要深入的探讨这个话题，我们首先要理解「什么是GO？」

01 GO的概念

GO (Gene Ontology)，中文译名为基因本体论。基因组测序已经清楚地表明，很大一部分规定核心生物功能的基因是所有真核生物共有的。一个生物体中这种共享蛋白质的生物学作用的知识往往可以转移到其他生物体中。基因本体论数据库的目标是产生一个动态的、受控的词汇，即使关于基因和蛋白质在细胞中的作用的知识在不断积累和变化，也可以应用于所有真核生物。为此，三个独立本体被构建：生物过程、分子功能和细胞成分。而这一过程始于1998，当时研究三种模式生物--黑腹果蝇、小鼠和酿酒酵母的基因组的研究人员同意就基因功能的共同分类方案进行合作，如今数十年过去，GO所代表的不同生物的数量已达数千。GO以一种灵活和动态的方式，为整个系统发育谱系中的同源基因和蛋白质序列提供了可比较的描述。

GO注释即是将基因产物与与GO term（术语）相联系的过程，在这个过程中，通过数据库比对等方法，一个物种的基因会有与之对应的GO术语，这形成了一个基因-GO术语的列表。GO注释最常见的用途是解释大规模的分子生物学实验，有时称为 "全能 "实验。无论是，基因组学、转录组学、蛋白质组学或代谢组学，这些实验汇集了生物分子，以获得对生物体结构、功能和动态的洞察力。"基因本体论富集分析 "被用来发现在交替控制的实验条件下的统计学上的重大相似性或差异。

02 GO富集分析的数学原理

在这里我们重点讨论GO富集分析。GO富集分析的数学原理基于超几何分布。超几何分布属于离散随机变量的概率分布。这里，我们首先理解几个「统计学概念」：

*定义1：随机变量Y是一个定义在样本空间上的数值函数，样本空间中的每一个简单事件都被指派一个Y值

举例来说明这个定义：从240件产品中随机选择4件产品进行检验，以确定这四件产品是否为有缺陷产品，如果有缺陷产品超过一件，则这240个产品都将被拒绝。在这个例子中，关心的事件是观测变量Y，Y表示被检验四件产品中有缺陷产品的数量。事件Y=0表示4件产品中没有缺陷产品的简单事件集合。Y的可能值是一个用数字表示的事件，称Y为一个随机变量。

同样在这个例子中，缺陷产品数量Y的取值个数是可数的，只可以取0，1，2，3，4这5个值中的一个，由此延申出定义2：

*定义2：离散随机变量Y是一个仅能取可数个值的变量

随机变量Y的可能取值是数值事件，我们希望计算事件的概率。这里给出定义3：

*定义3：随机变量Y的概率分布是给出Y的每个可能取值Y=y以及相应概率p(Y=y)的表、图或公式

了解这些定义后，我们回到一开始提出的超几何概率分布。

还是先举一个例子：实验室里一共摆放了10种试剂，这10种试剂种有4种是酸性试剂，6种是碱性试剂，现在随机抽取3种试剂，问，没有酸性试剂被抽中的概率。

本例中，随机变量Y表示选中酸性试剂的数量，这是一个典型的无放回抽样，Y是一个超几何随机变量，为了计算p(0)的概率，我们需要再引入「一个定理」：

*定理（组合法则）：一个n个元素的样本是从N个元素的集合中选择的，那么从N个中选择n个不同样本个数记作，它等于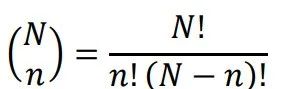

那么，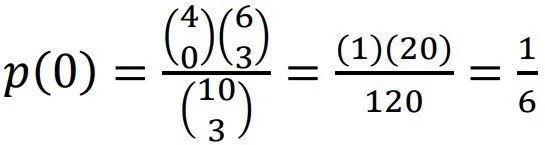

推广超几何概率分布公式：

在本例中，N=10，n=3，r=4，y=0。

现在，我们把应用场景切换到差异表达基因的GO功能富集上，假设某物种中有共有N个基因，这其中有r个基因与某一GO term对应（例如GO:0004046），每次抽取n个基因，那么，抽到和 GO:0004046相关的基因数量为y的概率，满足超几何概率分布。

在这个场景里，随机变量Y表示选中和 GO:0004046相关的基因数量，每次抽取n个基因相当于我们差异表达基因数量为n，若试验重复无数多次，即可观察到Y值的模型。

当然，这里得到的结果有可能是因为随机选择而导致的，也就是说随机变量Y的分布并不一定满足公式，只是因为我们每次恰好抽中了这么多的相关基因。

为此，我们要计算p值，阈值为p<0.05即为显著富集，但目前我们仅仅考虑差异基因富集到一条通路的情况，事实上在做GO富集分析时，基因在每一条通路上的富集都需要检验，这就需要利用多重检验来矫正p值，即最终p-adjusted<0.05才为显著富集。

03 GO富集分析的代码实现

讨论了GO富集分析的数学问题，再来进行GO富集分析的实践。在这我推荐使用南方医科大学Guangchuang Yu发表的R包clusterProfiler进行分析。详细代码如下：

library(clusterProfiler) #载入R包
library(tidyr)




genelist<-read.delim('DEGgenelist.txt',header = F) #读取差异表达基因的基因列表
genelist<- genelist$V1[1:nrow(genelist)]#genelist必须为vector




term2gene <-read.delim('term2gene.txt',header = T) #读取GO term和物种基因号对应的列表
term2name<-read.delim('term2name.txt',header = T) #读取GO term和term描述对应的列表




df <- enricher(gene = genelist, TERM2GENE = term2gene, TERM2NAME = term2name, pvalueCutoff = 0.05, qvalueCutoff = 0.05)
input<-df@result
input<-separate(input,GeneRatio,c('Study.term','Study.total'),sep = '\\/') #把GeneRatio的结果拆分
input<-separate(input,BgRatio,c('Pop.term','Pop.total'),sep = '\\/') #把BgRatio的结果拆分
go2ont <- go2ont(term2gene$GO)
mergedf<-merge(input,go2ont,by.x = 'ID',by.y = 'go_id',all.x = T)
write.table(mergedf,'GOEA.txt',quote = F,row.names = F,sep = '\t') #输出结果

04 GO富集分析结果的可视化

接下来进行可视化绘图，在此之前先讨论一个概念，什么是enrich factor富集因子。

富集因子=(某个term中出现的差异基因的个数/所有的差异基因的个数) / （term中包含的所有基因 / 数据库中总的基因数目）

回归我们前文提到的超几何分布，你就会发现，数据库中总的基因数目即为总数N，term中包含的所有基因即为r，所有的差异基因的个数即为抽样个数n，某个term中出现的差异基因的个数为随机变量数值y。

理解概念之后，我们开始绘制一个GO气泡图，代码如下：

library(ggplot2)




go<-read.delim("GOEA.txt", header = T, sep = "\t", check.names = T)
go <- go[go$p.adjust<0.05,]
go<-go[order(go$p.adjust,decreasing = T),]




gofold<-(as.numeric(go$Study.term)/as.numeric(go$Study.total))/(as.numeric(go$Pop.term)/as.numeric(go$Pop.total)) #计算enrich factor
gof<--log10(go$p.adjust)
Number <- go$Study.term




ggplot(go,aes(gofold,Description))+
  geom_point(aes(size=gof,color=Number))+
  scale_color_gradient(low = "#6a82fb", high = "#fc5c7d")+
  labs(color='Counts',alpha="Number of enriched genes",size="−log10(FDR)",x="Enrichment factor (fold)",y="",title="")+
  theme_bw()+theme(axis.line = element_line(colour = "black"), axis.text = element_text(color = "black",size = 14),legend.text = element_text(size = 14),legend.title=element_text(size=14),axis.title.x = element_text(size = 14))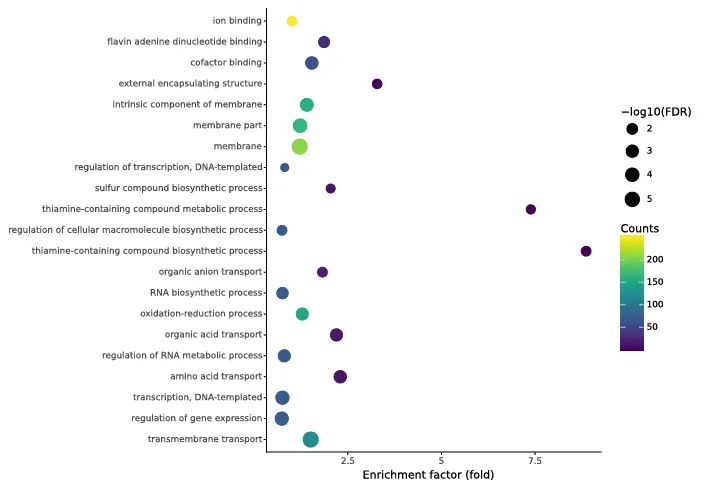

对GO的介绍就到这里了，GO与我们生物学实验往往息息相关，理解其中原理，可以帮助我们更好的掌握GO富集分析方法。

参考资料：

Ashburner, M., Ball, C. A., Blake, J. A., Botstein, D., Butler, H., Cherry, J. M., Davis, A. P., Dolinski, K., Dwight, S. S., Eppig, J. T., Harris, M. A., Hill, D. P., Issel-Tarver, L., Kasarskis, A., Lewis, S., Matese, J. C., Richardson, J. E., Ringwald, M., Rubin, G. M., & Sherlock, G. (2000). Gene ontology: tool for the unification of biology. The Gene Ontology Consortium. Nature genetics, 25(1), 25–29. https://doi.org/10.1038/75556

Yu G, Wang L, Han Y and He Q*. clusterProfiler: an R package for comparing biological themes among gene clusters. OMICS: A Journal of Integrative Biology. 2012, 16(5):284-287.

http://geneontology.org/

William M. Mendenhall and Terry L. Sincich. Statistics for Engineering and the Sciences

写在后面

为鼓励读者交流快速解决科研困难，我们建立了“宏基因组”讨论群，己有国内外6000+ 科研人员加入。请添加主编微信meta-genomics带你入群，务必备注“姓名-单位-研究方向-职称/年级”。高级职称请注明身份，另有海内外微生物PI群供大佬合作交流。技术问题寻求帮助，首先阅读《如何优雅的提问》学习解决问题思路，仍未解决群内讨论，问题不私聊，帮助同行。