『深度概念』原理图解代码FPN Feature Pyramid Networks

最新推荐文章于 2025-03-19 18:40:30 发布

小宋是呢

最新推荐文章于 2025-03-19 18:40:30 发布

阅读量1.5k

点赞数 3

分类专栏：深度学习概念

本文链接：https://blog.csdn.net/xiaosongshine/article/details/103289779

版权

深度学习概念专栏收录该内容

37 篇文章

订阅专栏

下面我们介绍一下特征金字塔网络。如下引用[1]

图(a)是相当常见的一种多尺度方法，称为featurized image pyramid,这种方法在较早的人工设计特征（DPM）时被广泛使用,在CNN中也有人使用过。就是对input iamge进行multi scale，通过设置不同的缩放比例实现。这种可以解决多尺度，但是相当于训练了多个模型（假设要求输入大小固定），即便允许输入大小不固定，但是也增加了存储不同scale图像的内存空间。
图(b)就是CNN了，cnn相比人工设计特征，能够自己学习到更高级的语义特征，同时CNN对尺度变化鲁棒，因此如图，从单个尺度的输入计算的特征也能用来识别，但是遇到明显的多尺度目标检测时，还是需要金字塔结构来进一步提升准确率。
从现在在imageNet和COCO数据集上领先的的一些方法来看，在测试的时候都用到了featurized image pyramid方法,即结合(a)，(b)。说明了特征化图像金字塔的每一级的好处在于，产生了多尺度的特征表示，每一级的特征都有很强的语义（因为都用cnn生成的特征），包括高分辨率的一级（最大尺度的输入图像）。
但是这种模式有明显的弊端，相比于原来方法，时间增长了4倍，很难在实时应用中使用，同样，也增大了存储代价，这就是为什么只是在测试阶段使用image pyramid。但是如果只在测试阶段使用，那么训练和测试在推断的时候会不一致。所以，最近的一些方法干脆舍弃了image pyramid。

但是image pyramid不是计算多尺度特征表示的唯一方法。deepCNN能够层次化的特征，而且因为池化的作用，会产生金字塔形的特征，具有一种内在的多尺度。但是问题在于，高分辨率的map（浅层）具有low-level的特征，所以浅层的目标识别性能较弱。这也是不同level融合的目的。

如图(c)，SSD较早尝试了使用CNN金字塔形的层级特征。理想情况下，SSD风格的金字塔重利用了前向过程计算出的来自多层的多尺度特征图，因此这种形式是不消耗额外的资源的。但是SSD为了避免使用low-level的特征，放弃了浅层的feature map，而是从conv4_3开始建立金字塔，而且加入了一些新的层。因此SSD放弃了重利用更高分辨率的feature map，但是这些feature map对检测小目标非常重要。这就是SSD与FPN的区别。
图(4)是FPN的结构，FPN是为了自然地利用CNN层级特征的金字塔形式，同时生成在所有尺度上都具有强语义信息的特征金字塔。所以FPN的结构设计了top-down结构和横向连接，以此融合具有高分辨率的浅层layer和具有丰富语义信息的深层layer。这样就实现了从单尺度的单张输入图像，快速构建在所有尺度上都具有强语义信息的特征金字塔，同时不产生明显的代价。

下面我们再来看一下相似的网络：

这里写图片描述

上面一个带有skip connection的网络结构在预测的时候是在finest level（自顶向下的最后一层）进行的，简单讲就是经过多次上采样并融合特征到最后一步，拿最后一步生成的特征做预测。而FPN网络结构和上面的类似，区别在于预测是在每一层中独立进行的。后面的实验证明finest level的效果不如FPN好，原因在于FPN网络是一个窗口大小固定的滑动窗口检测器，因此在金字塔的不同层滑动可以增加其对尺度变化的鲁棒性。另外虽然finest level有更多的anchor，但仍然效果不如FPN好，说明增加anchor的数量并不能有效提高准确率。

自下而上的路径

CNN的前馈计算就是自下而上的路径，特征图经过卷积核计算，通常是越变越小的，也有一些特征层的输出和原来大小一样，称为“相同网络阶段”（same network stage ）。对于本文的特征金字塔，作者为每个阶段定义一个金字塔级别，然后选择每个阶段的最后一层的输出作为特征图的参考集。这种选择是很自然的，因为每个阶段的最深层应该具有最强的特征。具体来说，对于ResNets，作者使用了每个阶段的最后一个残差结构的特征激活输出。将这些残差模块输出表示为{C2, C3, C4, C5}，对应于conv2，conv3，conv4和conv5的输出，并且注意它们相对于输入图像具有{4, 8, 16, 32}像素的步长。考虑到内存占用，没有将conv1包含在金字塔中。

自上而下的路径和横向连接

自上而下的路径（the top-down pathway ）是如何去结合低层高分辨率的特征呢？方法就是，把更抽象，语义更强的高层特征图进行上取样，然后把该特征横向连接（lateral connections ）至前一层特征，因此高层特征得到加强。值得注意的是，横向连接的两层特征在空间尺寸上要相同。这样做应该主要是为了利用底层的定位细节信息。

下图显示连接细节。把高层特征做2倍上采样（最邻近上采样法，可以参考反卷积），然后将其和对应的前一层特征结合（前一层要经过1 * 1的卷积核才能用，目的是改变channels，应该是要和后一层的channels相同），结合方式就是做像素间的加法。重复迭代该过程，直至生成最精细的特征图。迭代开始阶段，作者在C5层后面加了一个1 * 1的卷积核来产生最粗略的特征图，最后，作者用3 * 3的卷积核去处理已经融合的特征图（为了消除上采样的混叠效应），以生成最后需要的特征图。为了后面的应用能够在所有层级共享分类层，这里坐着固定了3*3卷积后的输出通道为d,这里设为256.因此所有额外的卷积层（比如P2）具有256通道输出。这些额外层没有用非线性。

{C2, C3, C4, C5}层对应的融合特征层为{P2, P3, P4, P5}，对应的层空间尺寸是相通的。

这里写图片描述

1 图解

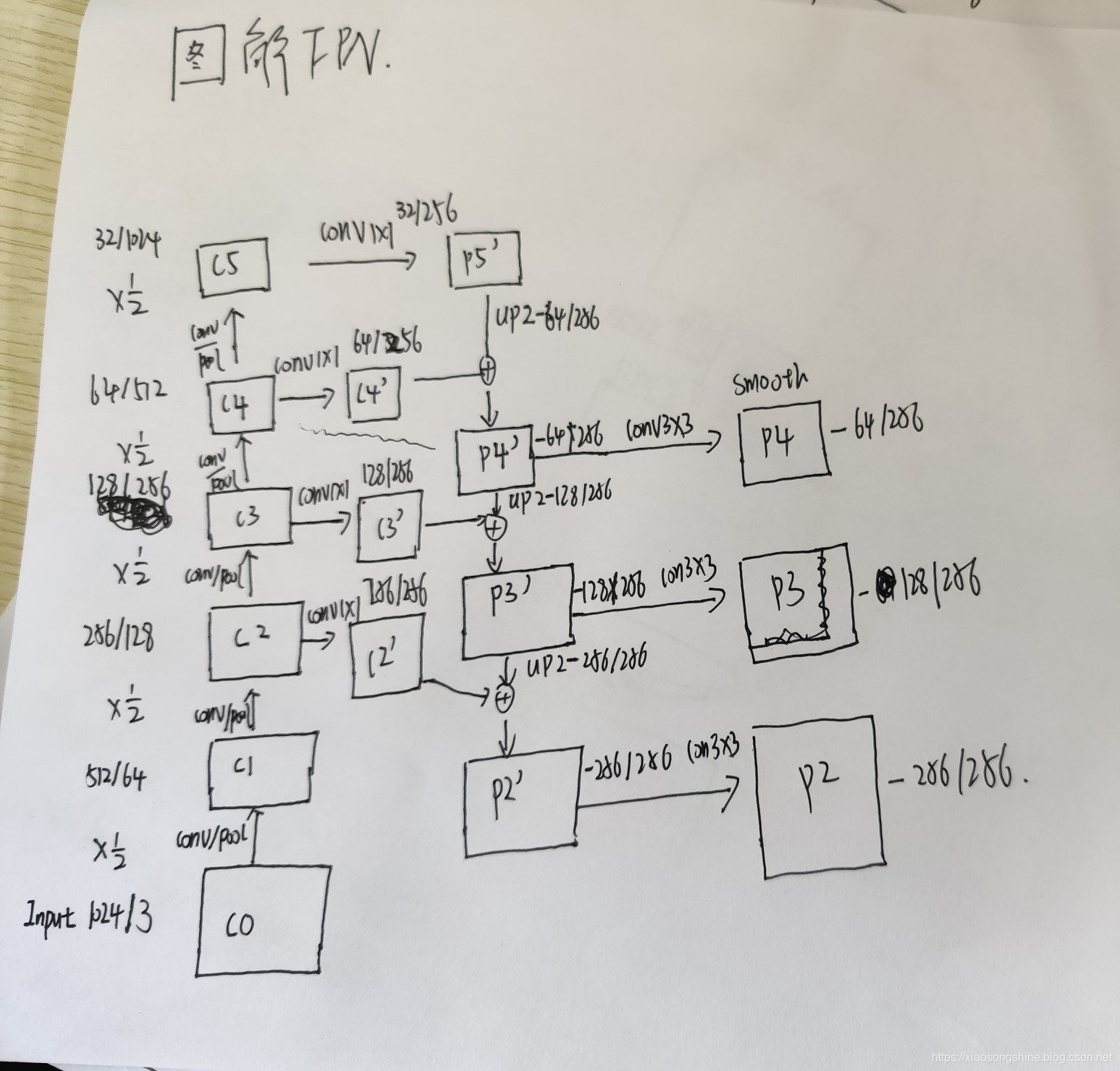
2 代码

'''FPN in PyTorch.
See the paper "Feature Pyramid Networks for Object Detection" for more details.
'''
import torch
import torch.nn as nn
import torch.nn.functional as F

from torch.autograd import Variable


class Bottleneck(nn.Module):
    expansion = 4

    def __init__(self, in_planes, planes, stride=1):
        super(Bottleneck, self).__init__()
        self.conv1 = nn.Conv2d(in_planes, planes, kernel_size=1, bias=False)
        self.bn1 = nn.BatchNorm2d(planes)
        self.conv2 = nn.Conv2d(planes, planes, kernel_size=3, stride=stride, padding=1, bias=False)
        self.bn2 = nn.BatchNorm2d(planes)
        self.conv3 = nn.Conv2d(planes, self.expansion*planes, kernel_size=1, bias=False)
        self.bn3 = nn.BatchNorm2d(self.expansion*planes)

        self.shortcut = nn.Sequential()
        if stride != 1 or in_planes != self.expansion*planes:
            self.shortcut = nn.Sequential(
                nn.Conv2d(in_planes, self.expansion*planes, kernel_size=1, stride=stride, bias=False),
                nn.BatchNorm2d(self.expansion*planes)
            )

    def forward(self, x):
        out = F.relu(self.bn1(self.conv1(x)))
        out = F.relu(self.bn2(self.conv2(out)))
        out = self.bn3(self.conv3(out))
        out += self.shortcut(x)
        out = F.relu(out)
        return out


class FPN(nn.Module):
    def __init__(self, block, num_blocks):
        super(FPN, self).__init__()
        self.in_planes = 64

        self.conv1 = nn.Conv2d(3, 64, kernel_size=7, stride=2, padding=3, bias=False)
        self.bn1 = nn.BatchNorm2d(64)

        # Bottom-up layers
        self.layer1 = self._make_layer(block,  64, num_blocks[0], stride=1)
        self.layer2 = self._make_layer(block, 128, num_blocks[1], stride=2)
        self.layer3 = self._make_layer(block, 256, num_blocks[2], stride=2)
        self.layer4 = self._make_layer(block, 512, num_blocks[3], stride=2)

        # Top layer
        self.toplayer = nn.Conv2d(2048, 256, kernel_size=1, stride=1, padding=0)  # Reduce channels

        # Smooth layers
        self.smooth1 = nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1)
        self.smooth2 = nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1)
        self.smooth3 = nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1)

        # Lateral layers
        self.latlayer1 = nn.Conv2d(1024, 256, kernel_size=1, stride=1, padding=0)
        self.latlayer2 = nn.Conv2d( 512, 256, kernel_size=1, stride=1, padding=0)
        self.latlayer3 = nn.Conv2d( 256, 256, kernel_size=1, stride=1, padding=0)

    def _make_layer(self, block, planes, num_blocks, stride):
        strides = [stride] + [1]*(num_blocks-1)
        layers = []
        for stride in strides:
            layers.append(block(self.in_planes, planes, stride))
            self.in_planes = planes * block.expansion
        return nn.Sequential(*layers)

    def _upsample_add(self, x, y):
        '''Upsample and add two feature maps.

        Args:
          x: (Variable) top feature map to be upsampled.
          y: (Variable) lateral feature map.

        Returns:
          (Variable) added feature map.

        Note in PyTorch, when input size is odd, the upsampled feature map
        with `F.upsample(..., scale_factor=2, mode='nearest')`
        maybe not equal to the lateral feature map size.

        e.g.
        original input size: [N,_,15,15] ->
        conv2d feature map size: [N,_,8,8] ->
        upsampled feature map size: [N,_,16,16]

        So we choose bilinear upsample which supports arbitrary output sizes.
        '''
        _,_,H,W = y.size()
        return F.upsample(x, size=(H,W), mode='bilinear') + y

    def forward(self, x):
        # Bottom-up
        c1 = F.relu(self.bn1(self.conv1(x)))
        c1 = F.max_pool2d(c1, kernel_size=3, stride=2, padding=1)
        print(f'c1:{c1.shape}')
        c2 = self.layer1(c1)
        print(f'c2:{c2.shape}')  

        c3 = self.layer2(c2)
        print(f'c3:{c3.shape}') 
        c4 = self.layer3(c3)
        print(f'c4:{c4.shape}') 
        c5 = self.layer4(c4)
        print(f'c5:{c5.shape}') 

        # Top-down
        p5 = self.toplayer(c5)
        print(f'p5:{p5.shape}') 
        p4 = self._upsample_add(p5, self.latlayer1(c4))
        print(f'latlayer1(c4):{self.latlayer1(c4).shape}, p4:{p4.shape}')

        p3 = self._upsample_add(p4, self.latlayer2(c3))
        print(f'latlayer1(c3):{self.latlayer2(c3).shape}, p3:{p3.shape}')

        p2 = self._upsample_add(p3, self.latlayer3(c2))
        print(f'latlayer1(c2):{self.latlayer3(c2).shape}, p2:{p2.shape}')

        # Smooth
        p4 = self.smooth1(p4)
        p3 = self.smooth2(p3)
        p2 = self.smooth3(p2)
        return p2, p3, p4, p5

def FPN101():
    # return FPN(Bottleneck, [2,4,23,3])
    return FPN(Bottleneck, [2,2,2,2])

def test():
    net = FPN101()
    fms = net(Variable(torch.randn(1,3,600,900)))
    for fm in fms:
        print(fm.size())

test()

输出：

c1:torch.Size([1, 64, 150, 225])
c2:torch.Size([1, 256, 150, 225])
c3:torch.Size([1, 512, 75, 113])
c4:torch.Size([1, 1024, 38, 57])
c5:torch.Size([1, 2048, 19, 29])
p5:torch.Size([1, 256, 19, 29])
latlayer1(c4):torch.Size([1, 256, 38, 57]), p4:torch.Size([1, 256, 38, 57])
latlayer1(c3):torch.Size([1, 256, 75, 113]), p3:torch.Size([1, 256, 75, 113])
latlayer1(c2):torch.Size([1, 256, 150, 225]), p2:torch.Size([1, 256, 150, 225])

# p2, p3, p4, p5
torch.Size([1, 256, 150, 225])
torch.Size([1, 256, 75, 113])
torch.Size([1, 256, 38, 57])
torch.Size([1, 256, 19, 29])