期权定价模型系列【14】期权复制—Delta动态复制误差计算

动态复制

直接使用期权进行对冲存在的问题之一是成本较高。假设我们多头一个看涨期权进行对冲，除本 身的交易费用之外，更多的隐性成本来自于期权的时间价值——期权价值等于内在价值与时间价值之 和，但在时间逐渐临近到期日的过程中，时间价值不断损耗，直至到期日为 0，如图 1 和图 2 所示。为 了降低对冲成本、改善对冲效果，可以采用复制投资组合的方法，通过调整标的资产的仓位，使复制 组合可以实现与期权相近的收益，从而在降低成本的同时，达到抓住上涨空间、对冲下跌风险的目的。

复制投资组合（Replication Portfolio）是指通过对一组资产进行配置，以模拟或复制特定的市场指 数、策略或投资组合的表现，使投资者能够在不直接购买指数成分股或实施策略的情况下获取相似的 投资回报。而期权也是一个可以复制的对象，我们可以通过配置期权标的资产和现金等实现对期权收益的复制。 
在介绍期权复制之前，我们首先要引入“中性”的概念。假设某一投资组合由期权、期权标的资 产和现金等构成，如果组合价值对标的资产价格的敏感性为 0，那么组合对标的资产价格就实现了“中 性”，而组合中标的资产和现金则完成了对期权的反向复制。 
为了获得期权对标的资产价格的敏感性，首先要对期权定价。Black-Scholes 模型是最常用的期权 定价公式，一单位看涨期权的价格可以表示为：

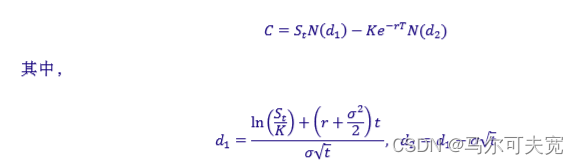
C 表示期权价格，N 表示标准正态分布，𝑆𝑡表示标的资产在 t 期的价格，K 表示期权的行权价格， r 表示无风险收益率， t 表示期权到期时间，𝜎表示标的资产收益率的波动率。那么，期权价格对标的资 产价格的敏感性 Delta 即可表示为： 

如果我们当前空头一单位看涨期权，同时多头 Delta 单位的标的资产，假设整个组合总资产为 V， 那么整个组合对标的资产价格的敏感性即为： 

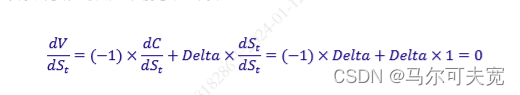
换而言之，无论未来标的资产价格上涨或下跌，整个组合的总资产都保持不变，即实现了“Delta 中性”；而多头 Delta 单位标的资产即等价于多头一单位看涨期权，这样我们就通过买入标的资产实现 了对期权的复制，这种期权复制方法又称“Delta 复制”。复制投资组合使我们在不直接多头期权的情 况下获取了相似的投资回报，同时规避了期权时间价值的损耗。 

根据调整频率，组合复制可以分为动态复制和静态复制。如果我们仅在期初调整标的资产仓位使 组合实现 Delta 中性、在未来不对标的资产进行调仓，则称为“静态复制”。静态复制简单、直观，调 仓频率低，但由于期权 Delta 会随着标的资产价格波动、到期时间临近等因素频繁变化，静态复制会导 致组合风险敞口较大。而动态复制会根据期权 Delta 的变化以日频或更高频率对组合中标的资产的仓 位进行动态调整，相比于静态复制风险敞口更小，实现的收益与期权收益更接近、复制效果更好。 

算法简介

我们将组合总损益除以障碍期权的初始理论价值，得到对冲损益百分比：

python实践：

if __name__=='__main__':
    opt=DeltaHedge(S=100, K=100,sigma=0.25,r=0.02,T=30,I=10000, Fre=1,fee=2/10000)
    # delta对冲
    ban=opt.balance()
    err=opt.HedgingError(ban)
    opt.Plot_Hist(err)

考虑手续费后的复制结果： 均值：-0.013978，标准差：0.54369。