机器人学/四足控制笔记（二）

书接上文，这边笔记主要介绍常用的正逆运动学解算方法，笔者按照自己的习惯，所有方法并没有全部介绍，而是介绍了两种笔者自己用在四足控制上的方法。

手臂几何描述

joint（关节） axis（轴） link（连杆）

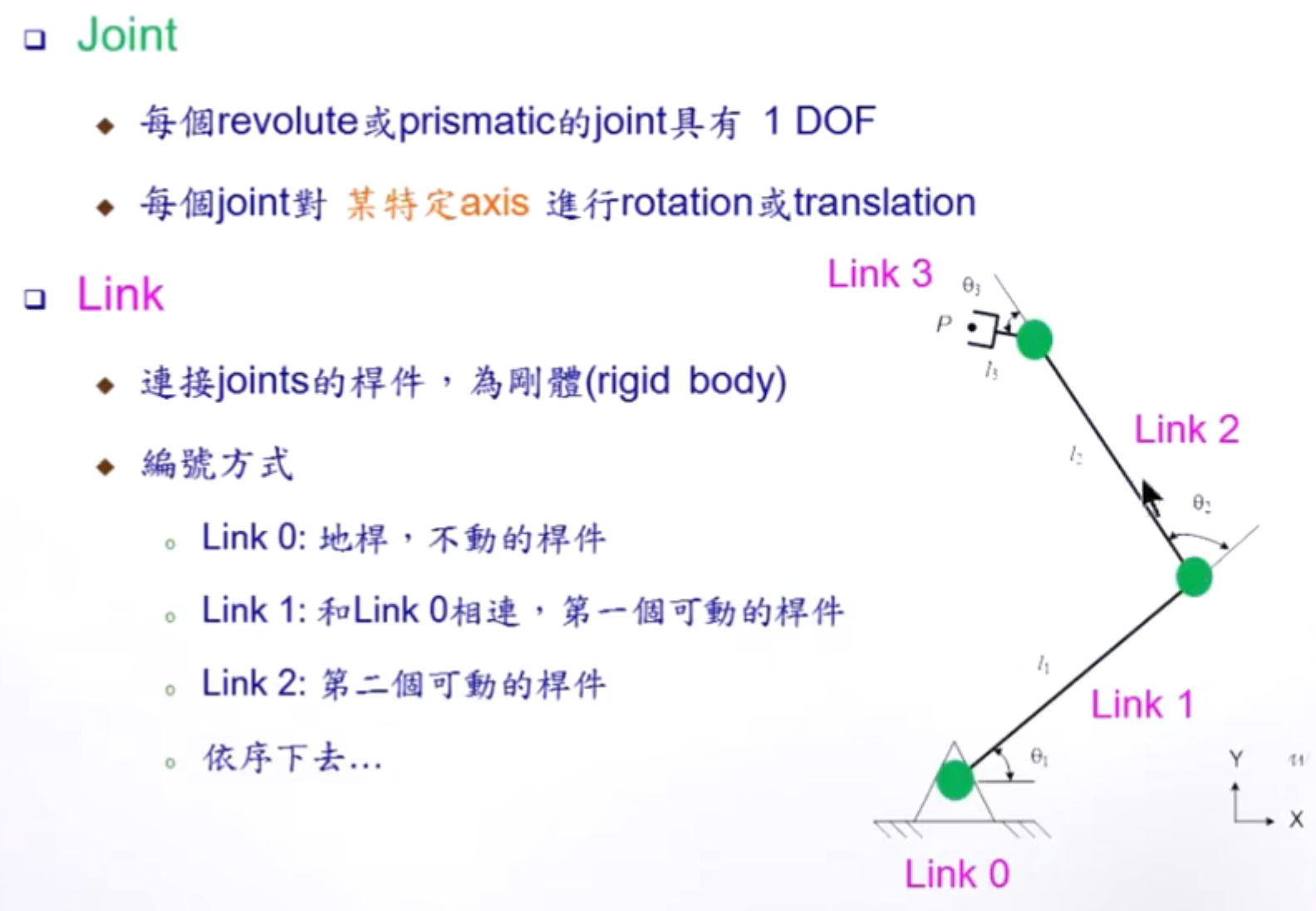
机器人运动学

机器人运动学解算可以说是所有简易运动控制算法的基础，通过运动学解算可以得到电机角度和末端执行器的关系，从而精确控制连杆移动，而运动学解算又分为两大类，正向运动学和逆向运动学。正向运动学简单来说就是已知电机转动角度求连杆或末端执行器的位置，逆向运动学就是已知连杆或者末端执行器的位置求电机转动角度。在运动控制算法中以逆运动学解算用的最多，因为一般都是获得末端执行器的目标点，然后要求机器人电机将末端执行器移动到相应位置。

正向运动学（Forward Kinematics）

正向运动学中比较通用的方法是Denavit-Hartenberg建模法（D-H建模法）。而在机器人的发展历程中又根据经典D-H建模法改良出了改良D-H建模法（Modified D-H method）也叫Craig Version。改良版比起经典D-H建模法来说解决了在串联腿或者树形结构等建模时出现的问题，而且相对运算量小，所以笔者主要介绍改良D-H建模法，对经典方法不做介绍。（注意：对于串联机器人来说正向运动学的解是唯一的，但是对于并联机器人来说则相反）

改良D-H建模法（Craig Version/Modified D-H method）

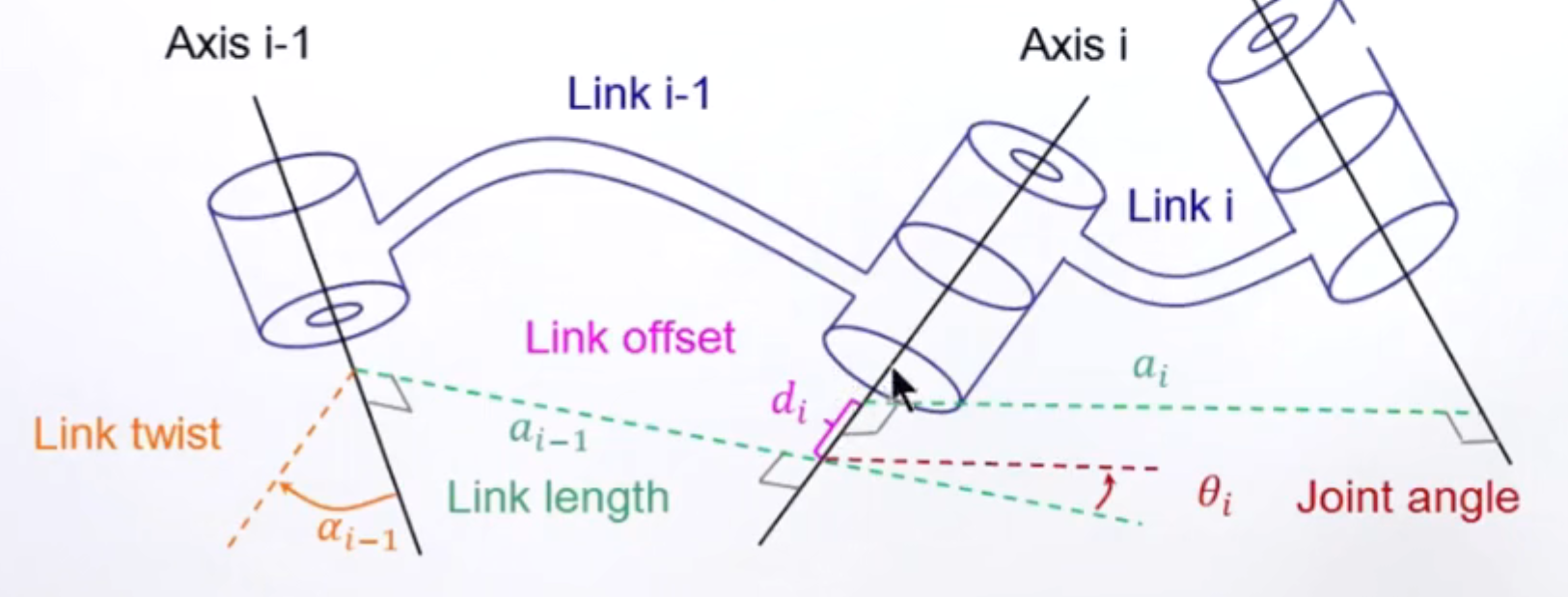
建模如上

：相邻两个轴i-1和i的夹角。

：相邻两个轴i-1和i的垂线距离（分清字母a和希腊字母（alhpa）的区别

:关节转动的角度，一般以Axis为z轴做笛卡尔坐标系后用两个坐标系的x轴夹角来表示。

：两个x轴在z轴上的距离。

建好模后接下来就是运动学正解的运算过程：

1. 首先将轴转动角度，使其与轴平行

2. 沿着轴的延长线平移距离

3. 将轴转动角度与轴重合

4. 最后沿着轴移动距离，与轴重合

公式表达如下：

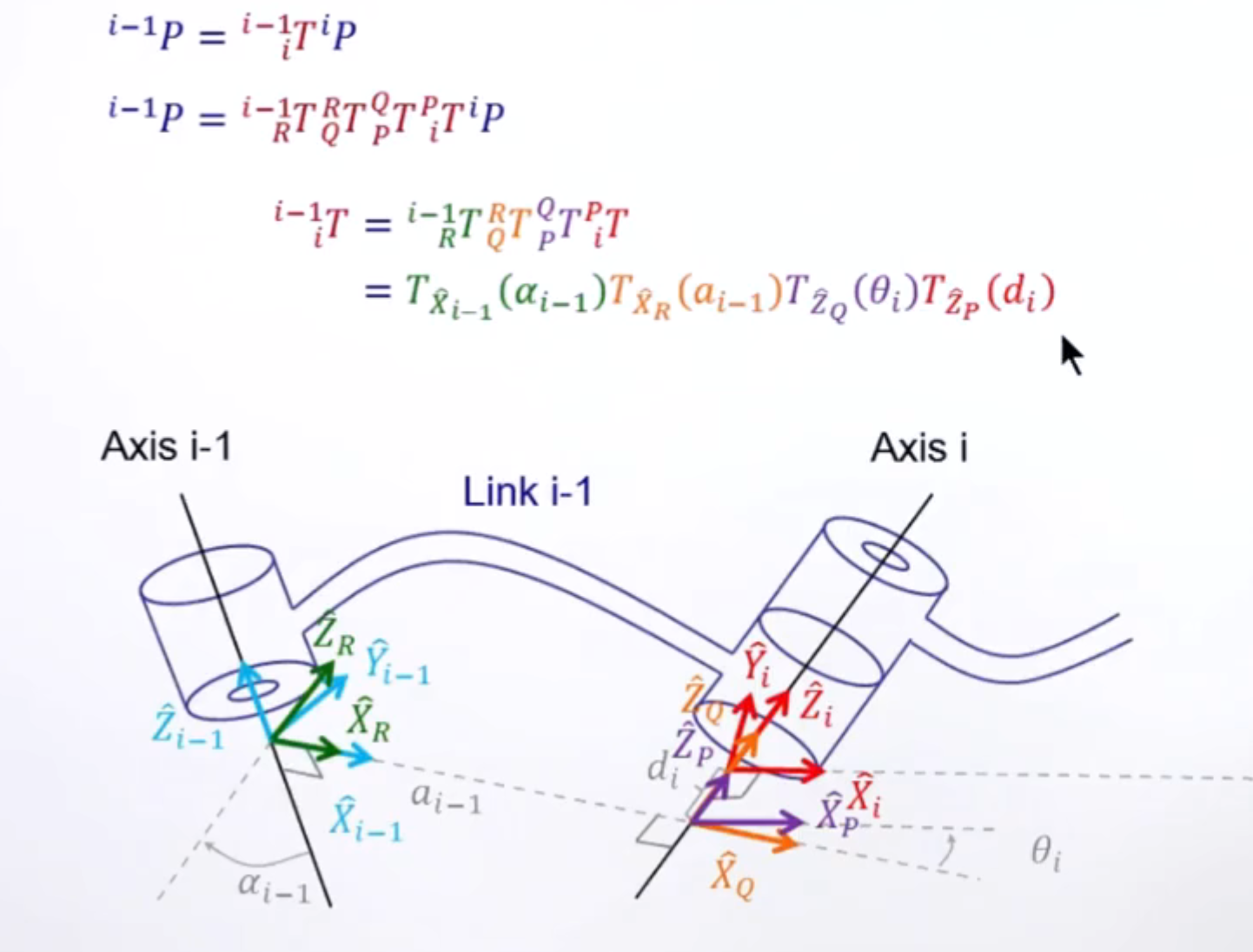
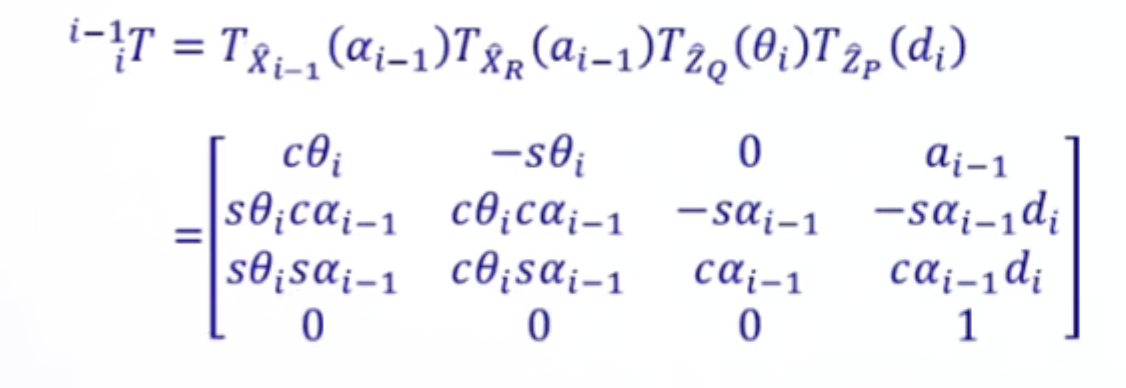
其中下标R，Q，P代表原轴经过变换后得到的新坐标轴。

下面举两个例子帮助大家熟悉

示例一：

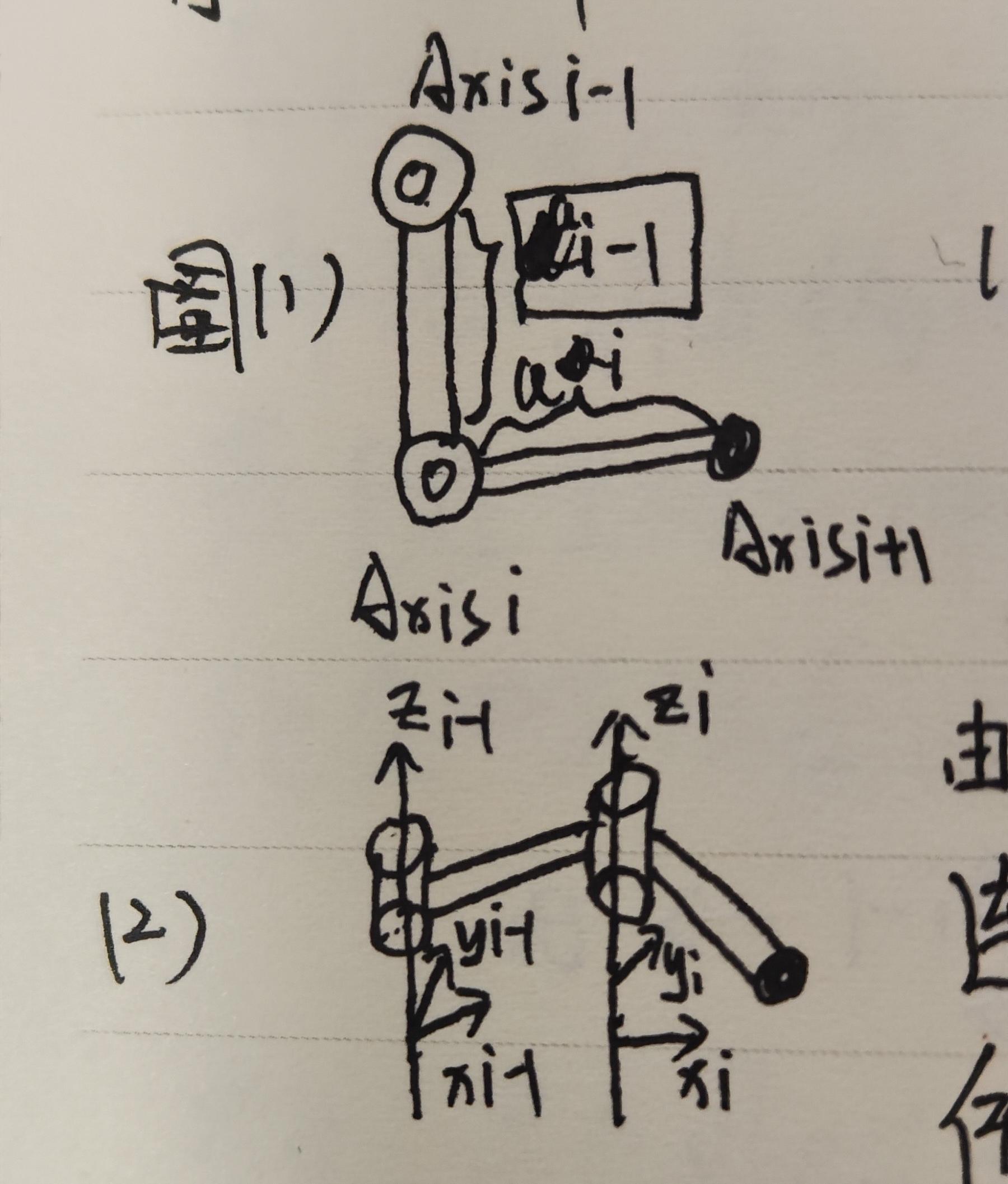
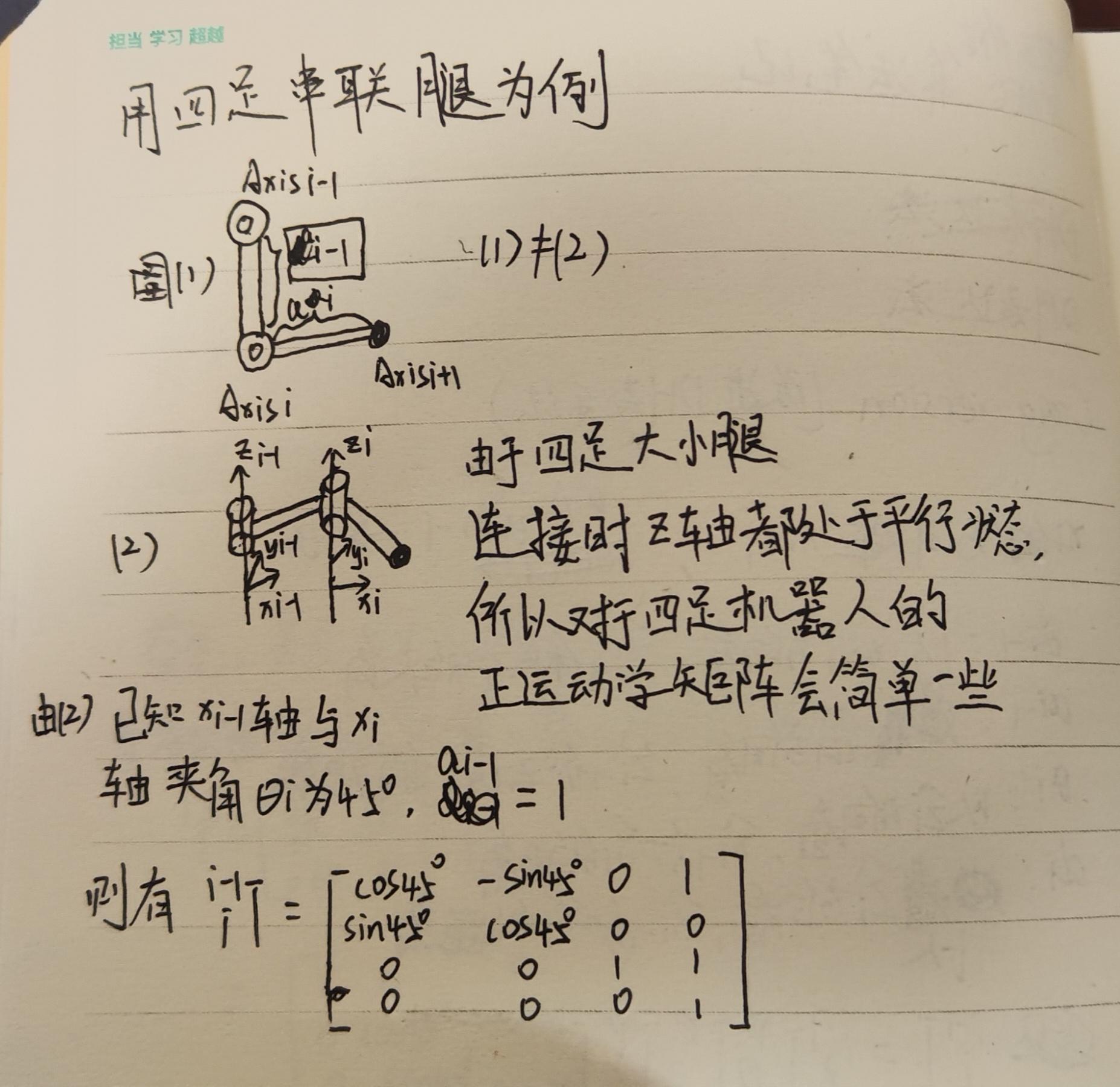
示例二：

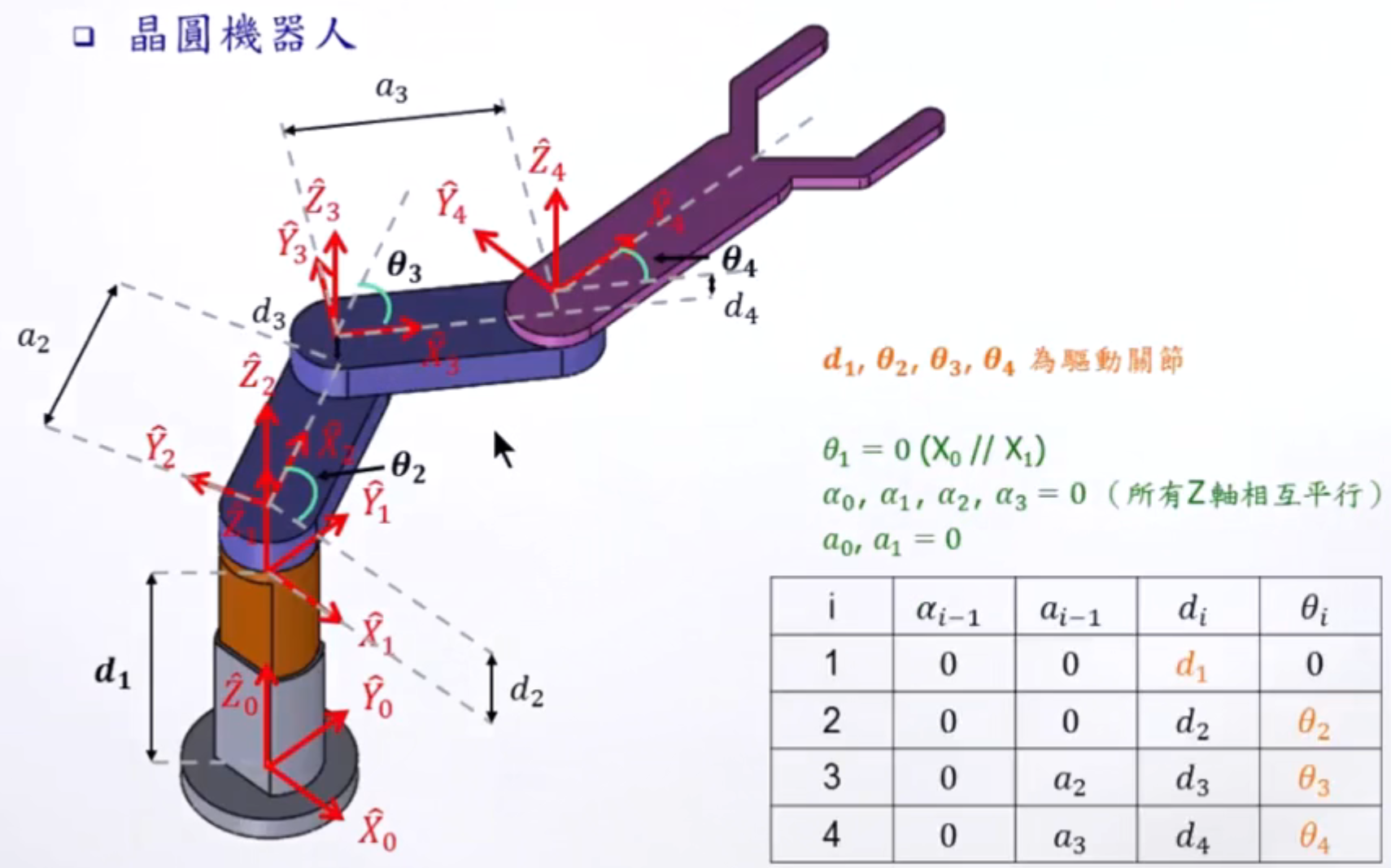
逆向运动学（Inverse Kinematics）

逆向运动学解算一般分为解析解和数值解，数值解就是通过反算连乘的旋转矩阵进行解算，但是算式较为复杂，所以在四足机器人的编程中一般使用的是解析解，也就是用几何方式进行解算。几何解法对机器人有相应要求，只有当相邻三轴（小于三轴就两轴）可以交于一点时，此结构才存在解析解，不过现在的机器人大多都满足这个条件，毕竟解析解的运算水平远远低于数值解。

几何解法的结构和算式如下图：

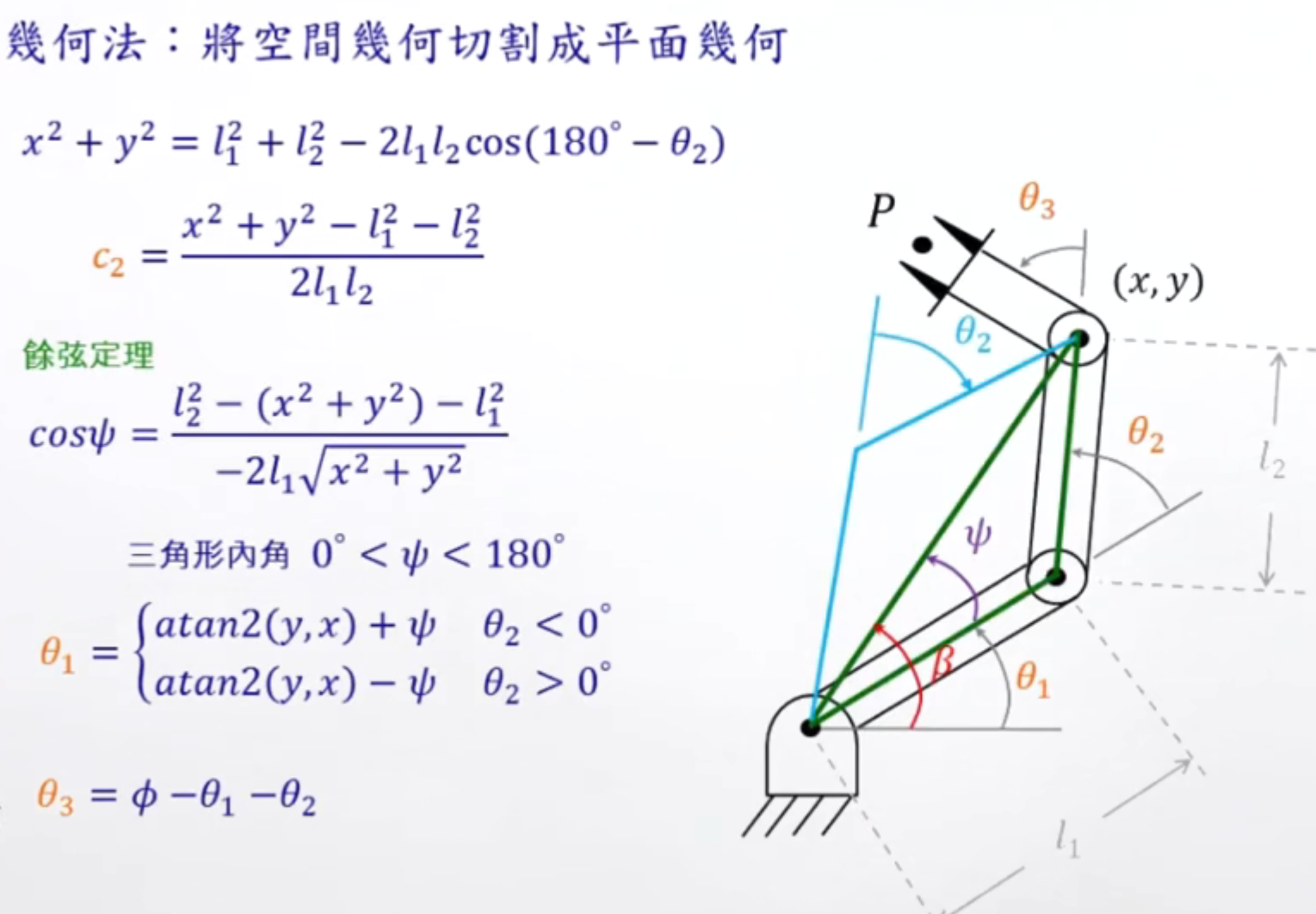
其中代表着末端执行器和水平面形成的夹角。

又因为四足只存在大小腿两个连杆，没有多余的部分，所以此时上图的theta3实际上为四足机器人的theta2，上图的theta2被省去，又因为笔者的四足机器人是并联腿，所以图中theta1的算式可以去掉，改为直接通过arcsin函数求解theta1。通过代码实现如图：

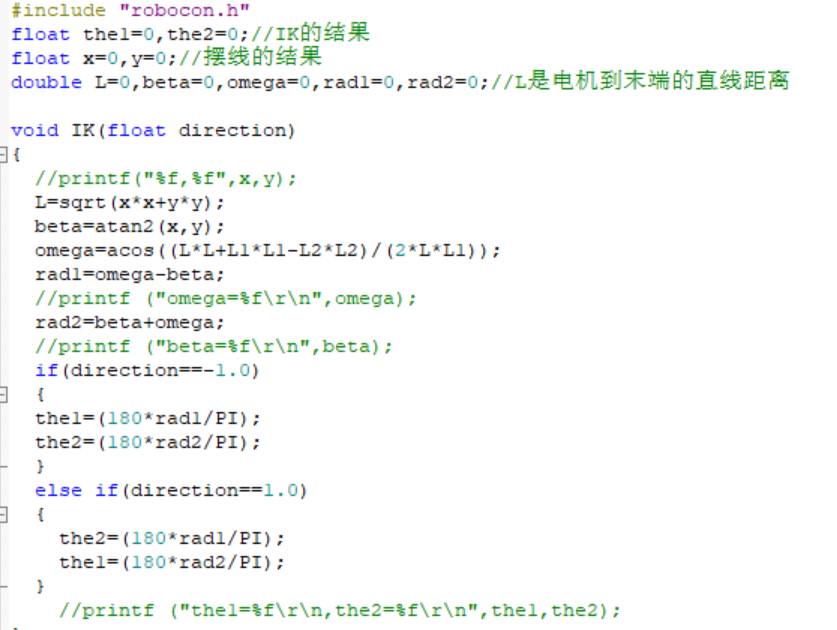
温馨提示：通过运算的得到的数据是弧度制，应该先转化为角度值再输入给电机。

结尾

这次的笔记以图片为主，主要是公式不好显示，然后如果发现有错误请及时指正，我会立马做出更改，下一次笔记会讲一下伪力控，也就是虚拟模型控制算法（VMC）或者进行机器人动力学的讲解，看笔者学习的速度，谢谢观看。