详细说DETR，基于transformer的目标检测相关原理，GIoU

详细说DETR，基于transformer的目标检测相关原理

GPT-4o

Poe

DETR (DEtection TRansformer)

DETR 是 Facebook AI Research (FAIR) 提出的一个端到端目标检测框架，它首次将 Transformer 架构 引入目标检测任务，为目标检测领域提供了一种新的范式。与传统目标检测方法（如 Faster R-CNN、YOLO 等）相比，DETR 抛弃了候选框生成、非极大值抑制（NMS）等复杂的后处理步骤，直接通过 Transformer 模型预测最终的目标边界框和类别。

以下是 DETR 的详细原理、架构和关键技术点的讲解。

---

1. DETR 的核心思想

1.1 端到端目标检测

传统目标检测方法（如 Faster R-CNN）的主要步骤包括：

1. 候选框生成（如 RPN 网络生成区域建议）。
2. 候选框分类和回归。
3. 通过非极大值抑制（NMS）移除冗余框。

然而，这些步骤是非端到端的，增加了复杂性。DETR 的目标是：

• 端到端检测：直接通过一个神经网络模型预测目标的边界框和类别，省去候选框生成和后处理步骤。
• Transformer：通过 Transformer 捕捉全局上下文信息，实现目标检测的全局建模。

---

2. DETR 的架构

DETR 的模型架构可分为以下几个部分：

2.1 Backbone (特征提取)

• 输入图像通过一个 卷积神经网络（CNN）（如 ResNet-50/101）提取多尺度特征。
• 输出特征图 F\mathcal{F}F 的维度为 C×H×WC \times H \times WC×H×W，其中 CCC 是通道数，HHH 和 WWW 是特征图的空间维度。

2.2 Transformer Encoder-Decoder

DETR 的核心是一个 Transformer 模块，包括 Encoder 和 Decoder，其作用是对特征图进行全局建模并输出目标信息。

(1) Transformer Encoder

• 接收来自 Backbone 的特征图 F\mathcal{F}F，将其展平为一维序列：

  Fflattened∈R(H⋅W)×C\mathcal{F}_{\text{flattened}} \in \mathbb{R}^{(H \cdot W) \times C}

• Fflattened​∈R(H⋅W)×C

• 

  每个像素位置的通道特征被视为一个输入 token。
• 加入 位置编码（Positional Encoding）：

  

• Finput=Fflattened+P\mathcal{F}_{\text{input}} = \mathcal{F}_{\text{flattened}} + \mathcal{P}

• Finput​=Fflattened​+P

  其中 P\mathcal{P}P 是位置编码，用于保留特征图的空间位置信息。
• 通过多层 Transformer Encoder 建模全局上下文关系，输出增强的特征序列。

(2) Transformer Decoder

• 输入包括：
  1. Learnable Queries：一组可学习的查询向量 Q∈RNq×dQ \in \mathbb{R}^{N_q \times d}Q∈RNq​×d（NqN_q通常是 100，表示最多检测 100 个目标）。
  2. Encoder 的输出特征序列。
• Decoder 通过多头注意力机制（Multi-Head Attention）和查询机制，逐步解码每个查询，预测目标的类别和边界框。

(3) Learnable Object Queries

• 查询向量 QQQ 是一组可学习的嵌入，表示潜在的目标对象。每个查询向量对应一个目标。
• 查询向量通过 Decoder 和 Encoder 特征交互，学习到目标的类别和位置。

---

2.3 预测头

• 类别预测：
  • 每个查询向量通过一个前馈神经网络（FFN）预测目标的类别（包括背景类 "no object"）。
• 边界框预测：
  • 每个查询向量通过另一个 FFN 预测目标的边界框。
  • 边界框的表示方式为 [x,y,w,h][x, y, w, h][x,y,w,h]，其中 (x,y)(x, y)(x,y) 是边界框中心，www 和 hhh 分别是宽度和高度。

---

3. DETR 的训练

DETR 的训练过程使用了以下关键技术：

3.1 匈牙利匹配（Hungarian Matching）

• 对于一个图像，模型会预测固定数量的查询（如 100 个）。
• 其中大部分查询可能没有对应的真实目标（即背景类 "no object"）。
• 使用 匈牙利算法 在预测的查询和真实目标之间找到最佳匹配：
  • 定义匹配代价：综合类别损失和边界框损失。
  • 通过最小化匹配代价找到预测结果和真实目标的最优匹配对。

3.2 损失函数

DETR 的总损失包括两部分：

1. 类别损失：
   • 使用交叉熵损失，计算预测类别与真实类别之间的误差。
2. 边界框损失：
   • 包括 L1 损失（定位误差）和 GIoU 损失（边界框形状误差）。

总损失公式为：

L=λcls⋅Lcls+λL1⋅LL1+λGIoU⋅LGIoU

\mathcal{L} = \lambda_{\text{cls}} \cdot \mathcal{L}_{\text{cls}} + \lambda_{\text{L1}} \cdot \mathcal{L}_{\text{L1}} + \lambda_{\text{GIoU}} \cdot \mathcal{L}_{\text{GIoU}}

L=λcls​⋅Lcls​+λL1​⋅LL1​+λGIoU​⋅LGIoU​

其中 λcls,λL1,λGIoU\lambda_{\text{cls}}, \lambda_{\text{L1}}, \lambda_{\text{GIoU}}λcls​,λL1​,λGIoU​ 是权重超参数。

---

4. DETR 的优点和挑战

4.1 优点

1. 端到端检测：

   • 无需候选框生成、非极大值抑制等后处理步骤。
   • 简化了检测流程。

2. 全局上下文建模：

   • Transformer 能够捕获全局依赖关系，特别是在复杂场景中，表现优于基于局部特征的方法。

3. 通用性强：

   • DETR 架构可以无缝扩展到其他任务（如实例分割、开放词汇检测）。

4.2 挑战

1. 训练效率低：

   • DETR 的训练收敛速度较慢，需要更长的训练时间（如 500+ epochs）。
   • 主要原因是 Transformer 需要大量数据才能充分学习全局关系。

2. 小目标检测表现较差：

   • 对于小目标，Transformer 的全局建模可能会弱化局部特征。

3. 高计算开销：

   • Transformer 的计算复杂度为 O(n^2)，随着特征图大小增加，计算量显著增长。

---

5. DETR 的改进版本

为了克服 DETR 的训练效率和小目标检测问题，研究者提出了多种改进版本：

5.1 Deformable DETR

• 引入 可变形注意力（Deformable Attention），在特征图上仅关注部分关键点，大幅降低计算复杂度。
• 显著提升了训练速度，同时改善了小目标检测性能。

5.2 Conditional DETR

• 改进了查询向量的初始化方式，使得模型能够更快地收敛。

5.3 DINO

• 增强了去噪机制（DeNoising Training），通过在训练过程中加入噪声样本，提升模型的鲁棒性。

---

6. DETR 的应用场景

1. 目标检测：

   • 在自然场景中检测目标物体的位置和类别。

2. 实例分割：

   • 扩展到实例分割任务，通过预测物体的边界轮廓。

3. 开放词汇检测：

   • 与视觉-语言模型（如 CLIP）结合，实现基于文本描述的目标检测。

4. 多任务学习：

   • 可扩展到其他视觉任务（如姿态估计、视频目标跟踪）。

---

7. 总结

DETR 的提出为目标检测领域带来了全新的思路：

• 它通过 Transformer 架构实现了端到端目标检测，抛弃了传统的候选框生成和后处理步骤。
• 虽然 DETR 存在训练效率低、高计算开销等问题，但后续的改进版本（如 Deformable DETR）已经显著提升了其实用性。

DETR 不仅是一种目标检测方法，更是将 Transformer 引入视觉任务的开创性工作，为视觉 Transformer 的发展奠定了基础。

详解DETR模型

已阅读 51 个网页

查看网页详情

DETR（Detection Transformer）是由Facebook在ECCV2020上提出的基于Transformer的端到端目标检测网络。以下是DETR模型的详细解释：

1. 模型架构：

   • Backbone：DETR使用卷积神经网络（如ResNet）作为backbone来提取图像的特征。这些特征被送入Transformer的encoder-decoder结构中。
   • Encoder：Encoder由多个Multi-Head Self-Attention和前馈神经网络（FFN）组成，对输入的特征进行转换和提取，得到特征图。每个Encoder都具有位置不变性，这是通过在Multi-Head Self-Attention中添加位置编码来实现的，以保证目标检测的位置敏感性。
   • Decoder：Decoder同样由多个Transformer层组成，它接收来自Encoder的特征图，并结合位置编码，输出目标的类别和边界框预测。
   • Detection Head：最后，模型通过两个线性层分别预测类别和边界框（xywh），这里会使用到额外的类别，即背景类。

2. 目标查询（Object Queries）：

   • DETR引入了目标查询的概念，这些是可学习的参数，通过其尺寸指定输出的预测框的个数。在Transformer中输出的token个数等于输出的目标查询的个数。

3. 全局上下文意识：

   • 由于Transformer使用自注意力机制，DETR可以捕获全局上下文，通过查看图像中其他对象的位置和关系来增强特征表示。

4. 简化的架构：

   • DETR通过一次性执行边界框和类别预测，消除了多阶段管道的需求，简化了目标检测的流程。

5. 二分图匹配和损失函数：

   • DETR使用匈牙利算法进行预测结果和ground-truth之间的匹配，并计算损失。这种基于匹配的损失有助于优化网络，使得预测和真实标注之间能够一一对应。

6. 训练与推理：

   • DETR的训练过程是端到端的，不需要额外的后处理步骤，如非极大值抑制（NMS）。这使得训练流程更简单、更高效。

7. 挑战与限制：

   • DETR需要大量的计算资源进行训练，特别是当数据规模庞大且包含高分辨率图像或骨干模型较大时。
   • 固定的物体查询数量可能限制了需要预测变化数量物体的场景。调整模型以动态处理不同物体数量是一个挑战。
   • 尽管DETR简化了训练流程，但由于Transformer架构的复杂性，推理速度可能比传统方法慢，使其不适用于实时用例。

DETR作为一种创新的目标检测框架，通过消除对许多人工设计组件的需求，如NMS或anchor生成，大大简化了目标检测的流程，并在COCO目标检测数据集上展示了与成熟且高度优化的Faster RCNN基线相当的准确性和运行时间。

详解DETR中的 GIoU 损失

GPT-4o

Poe

在 DETR（DEtection TRansformer） 中，GIoU（Generalized Intersection over Union）损失 是用于边界框回归的一个关键部分。GIoU 损失在目标检测任务中改进了传统的 IoU（Intersection over Union）指标，使其在边界框不重叠的情况下也能提供有效的梯度信号，从而更好地优化边界框的位置和形状。

以下是 GIoU 损失的详细原理、公式推导及其在 DETR 中的具体应用。

1. 传统 IoU 和其问题
1.1 IoU 的定义
IoU（Intersection over Union）是目标检测中常用的衡量预测边界框与真实边界框重叠程度的指标。其定义为：

​
 
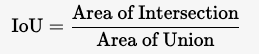
其中：

Intersection 是预测框和真实框的重叠区域面积。
Union 是预测框和真实框的并集面积。
IoU 的取值范围为 

[0,1]，数值越大表示预测框与真实框越接近。

1.2 IoU 的问题
无梯度问题：
当预测框和真实框完全没有重叠时，IoU = 0，无法提供有效的梯度信号，导致优化过程停滞。
忽略边界框的形状关系：
IoU 只关注重叠区域的比例，而对框的位置关系（如是否完全包含、是否接近）没有直接反映。例如，预测框和真实框虽然没有重叠，但它们可能非常接近，IoU 无法区分这种情况。
2. GIoU 的定义与改进
为了克服 IoU 的问题，GIoU（Generalized IoU） 被提出（论文：并集上的广义交集Generalized Intersection over Union）。GIoU 在 IoU 的基础上引入了一个补充项，考虑了预测框与真实框之间的空间关系。

2.1 GIoU 的公式
GIoU 的定义为：

​
 
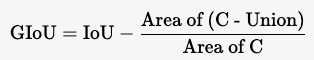
其中：

C
C 是包围预测框和真实框的最小闭包矩形（最小外接矩形）。
C - Union
C - Union 是闭包矩形面积减去预测框和真实框并集的面积。
2.2 GIoU 损失
为了将 GIoU 用作损失函数，定义 GIoU 损失 为：

当预测框完全等于真实框时，GIoU = 1，此时损失为 0。
当预测框和真实框完全不重叠时，GIoU 会小于 0，损失值大于 1。
3. GIoU 的优势
3.1 梯度信号在非重叠情况下仍然有效
即使预测框和真实框没有重叠（IoU = 0），GIoU 仍然可以通过 
Area of (C - Union)
Area of C
Area of C
Area of (C - Union)
​
  提供梯度信号，指导预测框向真实框靠近。

3.2 考虑位置和形状关系
GIoU 引入了最小外接矩形 
C
C，使得损失反映了预测框和真实框的位置关系。如果预测框接近真实框但没有重叠，GIoU 的值会变大，损失会减小，从而引导预测框向真实框的正确方向移动。

3.3 更高的收敛速度
相比 IoU 损失，GIoU 损失在边界框优化中的表现更加稳定，收敛速度更快，特别是在边界框初始化较差的情况下。

4. GIoU 损失在 DETR 中的应用
在 DETR 中，边界框的预测是通过 Transformer Decoder 的输出完成的，每个查询（Query）会预测一个边界框 
(
𝑥
,
𝑦
,
𝑤
,
ℎ
)
(x,y,w,h)，其中：

(
𝑥
,
𝑦
)
(x,y) 是边界框中心的坐标。
𝑤
,
ℎ
w,h 是边界框的宽度和高度。
4.1 目标匹配（匈牙利匹配）
DETR 使用匈牙利算法将每个预测框与真实框进行一一匹配。
在匹配过程中，GIoU 被用作匹配代价的一部分，以衡量每个预测框与真实框之间的空间关系。
4.2 回归损失
在边界框回归任务中，DETR 使用了两种损失：

L1 损失：用于直接优化预测框和真实框的坐标差异。
𝐿
L1
=
∥
𝑏
pred
−
𝑏
gt
∥
1
L 
L1
​
 =∥b 
pred
​
 −b 
gt
​
 ∥ 
1
​
 
其中 
𝑏
pred
b 
pred
​
  是预测框，
𝑏
gt
b 
gt
​
  是真实框。
GIoU 损失：用于优化预测框在空间上的重叠程度和位置关系。
𝐿
GIoU
=
1
−
GIoU
(
𝑏
pred
,
𝑏
gt
)
L 
GIoU
​
 =1−GIoU(b 
pred
​
 ,b 
gt
​
 )
4.3 总损失函数
DETR 的边界框回归损失是 L1 损失和 GIoU 损失的加权和：

𝐿
bbox
=
𝜆
L1
⋅
𝐿
L1
+
𝜆
GIoU
⋅
𝐿
GIoU
L 
bbox
​
 =λ 
L1
​
 ⋅L 
L1
​
 +λ 
GIoU
​
 ⋅L 
GIoU
​
 
𝜆
L1
λ 
L1
​
  和 
𝜆
GIoU
λ 
GIoU
​
  是超参数，控制两个损失的权重。
默认情况下，L1 损失和 GIoU 损失共同优化边界框的位置和形状。
5. GIoU 的数学直观理解
GIoU 的目标是综合考虑：

预测框与真实框的重叠（通过 IoU）。
预测框与真实框的空间接近程度（通过外接矩形 C 的约束）。
5.1 极端情况分析
完全重叠：
当预测框与真实框完全重叠时：
IoU
=
1
,
GIoU
=
1
−
Area of (C - Union)
Area of C
=
1
IoU=1,GIoU=1− 
Area of C
Area of (C - Union)
​
 =1
损失为 0。
无重叠但接近：
当预测框与真实框没有重叠，但接近时：
IoU
=
0
,
GIoU
>
0
IoU=0,GIoU>0
此时 GIoU 提供有效的梯度，推动预测框向真实框移动。
远离真实框：
当预测框远离真实框时，最小外接矩形 
𝐶
C 面积较大，
GIoU
GIoU 的值会下降，损失增大，指导模型优化。
6. 总结
GIoU 损失的作用：
弥补了 IoU 损失在边界框不重叠时的梯度问题。
考虑了边界框的空间位置关系，使得优化过程更加稳定和高效。
GIoU 在 DETR 中的应用：
用于目标匹配（匈牙利算法）和边界框回归优化。
与 L1 损失结合，共同提升边界框的定位精度。
优势：
提供有效的梯度信号，即使边界框不重叠。
改善边界框的定位和形状预测，特别是在复杂场景中。
通过 GIoU 损失，DETR 在边界框回归任务中展现了更高的鲁棒性和收敛速度，这也是其端到端检测能力的重要保障。