机器人控制系列教程之位置与姿态的描述(1)

工业小说家

已于 2024-05-27 21:11:28 修改

阅读量1k

点赞数 13

分类专栏：机器人控制系列教程文章标签：机器人算法

于 2024-05-27 20:59:26 首次发布

本文链接：https://blog.csdn.net/2301_78660208/article/details/139247482

版权

机器人控制系列教程专栏收录该内容

4 篇文章 0 订阅

订阅专栏

位置描述

笛卡尔坐标系下的位置描述

对于直角坐标系{A}来说，在空间任一点p的位置可用3x1的列矢量表示，即：
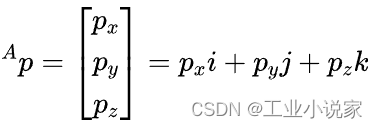
在这里插入图片描述
位置矢量 $^Ap$ 的模。模为1的位置矢量，称为单位位置矢量。

柱面坐标系下的位置描述

柱面坐标系下，采用点M在笛卡尔坐标系下的Z轴的位置分量矢量在XOY平面的投影长度r以及该投影与X轴的夹角 $\theta$ 表示。

将柱面坐标下的位置记为 $Cyl({p_z},\theta ,r)$ ，经化简可得：
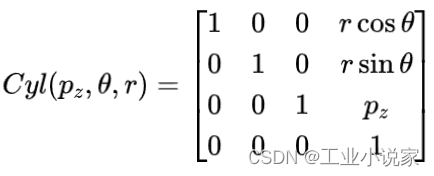
在这里插入图片描述

球面坐标系下的位置描述

球面坐标系下，采用点p在笛卡尔坐标系下的矢量模长r、矢量在XOY平面的投影与X轴的夹角$\theta $、矢量与 Z 轴的夹角$ \phi$表示。
在这里插入图片描述

姿态描述

在笛卡尔坐标系下，可以使用固定在物体上的坐标系描述方位(orientation)，亦称姿态(pose)。但对于一个普通刚体，常用的姿态描述包括笛卡儿坐标系下使用旋转矩阵的姿态描述、使用欧拉角(Euler)的姿态描述、使用横滚、俯仰、偏转角(Roll、Pitch、Yaw，RPY)的姿态描述等。
设空间中一刚体B，有直角坐标系{B}与此刚体固连，如下图所示，使用与{B}的坐标轴平行的三个单位矢量 ${}^A{x_B}$ 、 ${}^A{y_B}$ 及 ${}^A{z_B}$ 表示刚体B在基坐标系中的姿态，坐标系{A}、{B}亦称为坐标系或框{A}、{B}。坐标系{B}的三个单位主矢量相对于坐标系{A}的方向余弦组成的3x3的余弦矩阵来表示刚体B相对于坐标系{A}的方位：

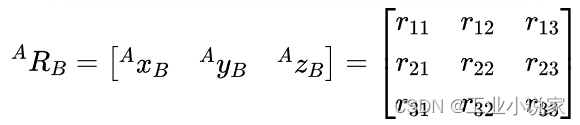
在这里插入图片描述

$^A{R_B}$ (亦或表示为 $^A_B{R}$ )称之为刚体B相对于坐标系{A}的姿态的旋转矩阵。 $^A{R_B}$ 中有9个元素，其中只有3个是独立的。因为其中三个列矢量均为单位主矢量，且两两相互垂直，其满足正交条件和单位模长约束，即：

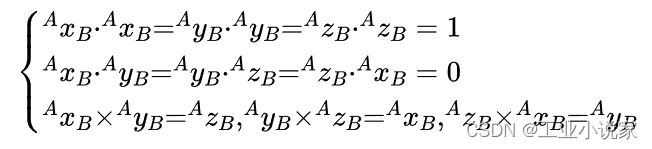
在这里插入图片描述

同时，该旋转变换矩阵的逆(反)变换等于其转置，也即满足如下条件：

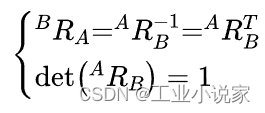
在这里插入图片描述

利用旋转矩阵的姿态描述

我们可以用相对参考坐标系的坐标轴单位向量表示它们所在坐标系的方向。每个单位向量有3个元素，它们组成了3*3阶正交矩阵 $^A{R_B}$ ：
在这里插入图片描述
$^A{R_B}$ 为表示刚体B相对于坐标系{A}的姿态的旋转矩阵，分别绕x、y、z轴旋转角后的标准正交旋转矩阵可表示为：

在这里插入图片描述

其中，$c\theta = \cos \theta $，$ s\theta = \sin \theta $。MATLAB工具箱中提供了基本函数来计算这些基本的旋转矩阵，如：

% 表示绕X、Y、Z轴旋转90°；
R1=rotx(90)
R2=roty(90);
R3=rotz(90);
% 绘制相应的坐标系；
trplot(R1)
trplot(R2)
trplot(R3)
% 绘制旋转动画
view([32.9 27.3]) % 设置相机视角方位角和仰角
tranimate(R1)
tranimate(R2)
tranimate(R3)

（插入RTB安装文档，并插入动图）

利用Euler的姿态描述

欧拉旋转定理要求绕3个轴依次旋转，但不能绕同一个轴线连续旋转两次。旋转顺序分为两种：欧拉式和卡尔丹式。欧拉式是绕一个特定的轴重复旋转，但不是连续的：XYX、XZX、YXY、YZY、ZXZ、ZYZ；卡尔丹式是绕三个不同轴旋转：XYZ、XZY、YZX、YXZ、ZXY、ZYX。一般来说，所有这些序列均被称为欧拉角，共有12种形式可以选择。通常将这12种旋转方式统称为欧拉角，但这一称呼并不够严谨。在某一特定的领域内，所说的欧拉角往往指某一种特定的旋转角顺序。
在机械动力学、机器人学、航空领域中，通常采用的是ZYZ序列的欧拉角，可以认为在笛卡儿坐标系的基础上，先绕Z轴旋转角度𝛼，再绕新的Y轴旋转角度𝛽，再绕新的Z轴旋转角度𝛾。旋转角度𝛼、𝛽、𝛾称为欧拉角，用以表示所有的姿态，欧拉变换在基坐标中表示为：

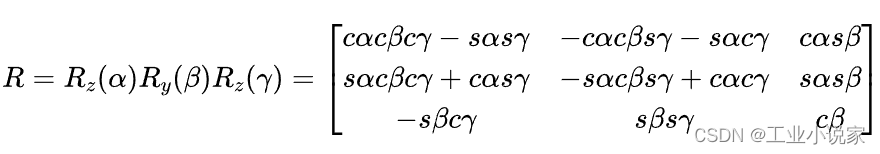
在这里插入图片描述
其中，$c\alpha = \cos \alpha $，$ s\alpha = \sin \alpha $，$ c\beta = \cos \beta $，$ s\beta = \sin \beta $，$ c\gamma = \cos \gamma $，$ s\gamma = \sin \gamma $。MATLAB的机器人工具箱中也是使用了这种方式的序列，我们可以这样写：

R=rotz(0.1)*roty(0.2)*rotz(0.3)
% 或者：
R1=eul2r(0.1,0.2,0.3)
% 上述问题的逆命题可以通过如下方式找到。
gam=tr2eul(R1,'deg')

% 若：
R2=eul2r(0.1,-0.2,0.3)
gam1=tr2eul(R2,'deg')

R3=eul2r(0.1,0,0.3)
gam1=tr2eul(R3,'deg')

上述可得，两组不同的欧拉角对应同一个旋转矩阵，说明从旋转矩阵到欧拉角的映射是不唯一的，而MATLAB工具箱函数返回的角度$ \beta $始终为正，对于$ \beta $=0的情况，实际上是一个奇异点，工具箱将其处理为：
${R_z}(\alpha ){R_z}(\gamma ) = {R_z}(\alpha + \gamma )$

利用RPY的姿态描述

RPY角(横滚-俯仰-偏航，旋转方式：卡尔丹角ZYX)通常用于船舶、飞机和车辆的姿态时非常直观，它是利用RPY描述刚体的姿态，可以认为在笛卡儿坐标系的基础上，先绕Z轴旋转角度，再绕新的Y轴旋转角度𝛽，再绕新的x轴旋转角度𝛾。旋转角度𝛼、𝛽、𝛾称为RPY角，用以表示所有的姿态，PRY变换在基坐标系中可表示为：
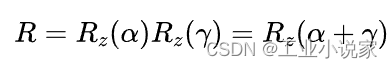
在这里插入图片描述

利用RPY的姿态描述

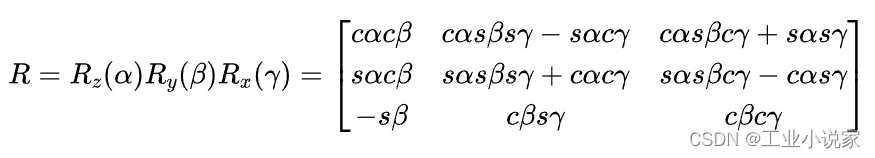
MATLAB工具箱可进行如下验证：

R=rpy2r(0.1,0.2,0.3)
gam=tr2rpy(R,'deg')

RPY序列允许每个角度值有任意正负号，不会产生多解的情况，但它也有奇异点，即当 $\beta = \pm \pi /2$ ，不过这个点在大多数载具的姿态范围之外，

利用四元数的姿态描述

见：http://mp.weixin.qq.com/s?__biz=MzU2OTUxNTA1OQ==&mid=2247487571&idx=1&sn=7d8ef836b37a29fb1b9b8dd799dbb7b4&chksm=fcfcdd0fcb8b54197cc59776d50b717e2b223f272b815d685591e562bacd27f3932fe35128b1&scene=21#wechat_redirect

$\left\| {{}^Ap} \right\| = \sqrt {p_x^2 + p_y^2 + p_z^2}$
在这里插入图片描述