作者 | 笑看雾里 编辑 | 汽车人
原文链接：https://www.zhihu.com/question/473480923/answer/3206057022
点击下方卡片，关注“自动驾驶之心”公众号
ADAS巨卷干货，即可获取
点击进入→自动驾驶之心【规划控制】技术交流群
本文只做学术分享，如有侵权，联系删文
论文：B. Zhou, F. Gao, L. Wang, C. Liu and S. Shen, “Robust and Efficient Quadrotor Trajectory Generation for Fast Autonomous Flight,” in IEEE Robotics and Automation Letters, vol. 4, no. 4, pp. 3529-3536, Oct. 2019, doi: 10.1109/LRA.2019.2927938.
文章的模块组成可分成以下几个部分：
包括了前端 kinodynamic a_star 路径搜索（在控制空间进行motion primitive）以及基于帕特利亚金最小值原理的两点边界值问题求解（解决控制空间稀疏采样无法抵达目标点的问题-在状态空间进行motion primitive）。
后端首先利用 均匀B样条曲线 对前端得到的路径进行拟合，之后基于距离场地图（ SDF ）对轨迹平滑性（纯几何性质，不是控制的Norm的时间积分，因为之后还要对时间进行调整），离障碍物距离，速度加速度超限等进行软约束优化。
得到优化的轨迹过后，使用 非均匀B样条曲线 对轨迹进行表达，然后对每一段超过速度，加速度上界的曲线进行时间节点的迭代调整，直到该段曲线的速度加速度符合约束。
一. kinodynamic a_star（前端hybrid A_star动力学路径搜索）
主要对应的是Fast planner->path ->path_searching->kinodynamic a_star.cpp。路径搜索的主要函数为kinodynamicAstar类的search函数，我们从这一函数开始阅读并逐一分析其中的重要函数：
search函数的参数包含起始点以及重点的位置，速度，加速度。以及两个标志位init 和dynamic，还有一个搜索起始时间。上图代码中主要是将起始点及目标点的三维位置转化至栅格地图的index. 并计算第一个扩展点的Heuristic cost.
1.1启发函数的计算
estimateHeuristic（）是第一个重要的函数，对应文章中的III.B小节，主要原理是利用庞特里亚金原理解决两点边值问题，得到最优解后用最优解的控制代价作为启发函数。
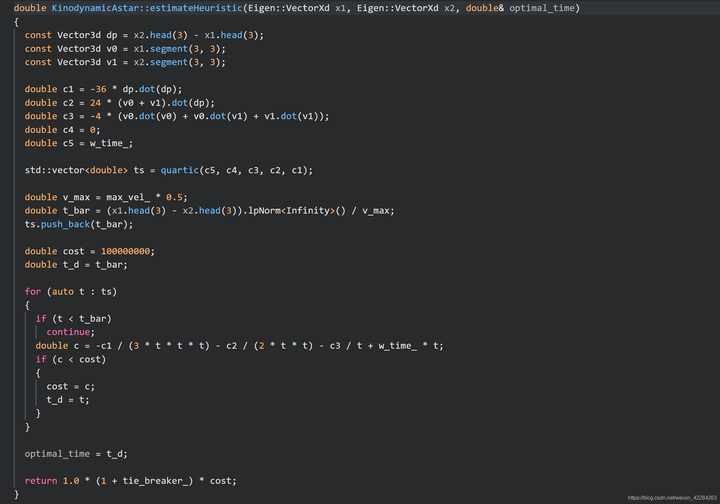首先通过设置启发函数对时间求导等于0，得到启发函数关于时间T的四次方程，再通过求解该四次方程，得到一系列实根，通过比较这些实根所对应的cost大小，得到最优时间。这里需要注意，关于时间的一元四次方程是通过费拉里方法求解的，需要嵌套一个元三次方程进行求解，也就是代码中应的cubic（）函数。
一元四次方程的求解过程参见wikipedia中的费拉里方法：
zh.wikipedia.org/wiki/%E5%9B%9B%E6%AC%A1%E6%96%B9%E7%A8%8B
一元三次方程的求见过程参见wikipedia中的求根系数法。需要加以说明的是，代码中的判别式大于0及等于0的情况利用了求根公式，判别式小于0的情况则是使用了三角函数解法：
zh.wikipedia.org/wiki/%E4%B8%89%E6%AC%A1%E6%96%B9%E7%A8%8B
1.2 Compute shot Traj
计算出起始节点的启发项后，就基本进入搜索循环，第一步是判断当前节点是否超出horizon或是离终点较近了，并计算一条直达曲线，检查这条曲线上是否存在。若存在，则搜索完成，返回路径点即可。
这里我们遇到了第二个重要的函数ComputeShotTraj. 即利用庞特里亚金原理解一个两点边值问题。因为最优控制时间已经在estimateHeuristic中计算过了，所以这里只要引入该时间进行多项式计算即可。这部分的目的是为了验证该轨迹是安全的，即不发生碰撞，速度、加速度不超限。
1.3 节点扩张
以上代码search()中，在当前节点的基础上，根据对输入、时间的离散进行扩展得到tmp临时节点，首先判断节点是否已经被扩展过，是否与当前节点在同一个节点，检查速度约束，检查碰撞，都通过的话，就计算当前节点的g_score以及f_score. 其中的state transit函数即通过前向积分得到扩展节点的位置和速度。接下来，就要进行节点剪枝。
1.4 节点剪枝
首先判断当前临时扩展节点与current node的其他临时扩展节点是否在同一个voxel中，如果是的话，就要进行剪枝。要判断当前临时扩展节点的fscore是否比同一个voxel的对比fscore小，如果是的话，则更新这一Voxel节点为当前临时扩展节点。
如果不剪枝的话，则首先判断当前临时扩展节点pro_node是否出现在open集中，如果是不是的话，则可以直接将pro_node加入open集中。如果存在于open集但还未扩展的话，则比较当前临时扩展节点与对应VOXEL节点的fscore,若更小，则更新voxel中的节点。
需要进行说明的是，在Fast planner的实现中，open集是通过两个数据结构实现的，一个队列用来存储，弹出open集中的节点。另一个哈希表NodeHashtable 用来查询节点是否已经存在于open集中。而判断一个节点是否存在于close set中，则是通过Nodehashtable 与nodestate来决定的，如果nodeState 是 InCloseSet, 且存在于NodeHashtable, 则说明该节点已经被扩展过了，存在于close set中。
1.5 返回kinopath与 getsamples
getKinoTraj这一 函数多作用是在完成路径搜索后按照预设的时间分辨率delta_t通过节点回溯和状态前向积分得到分辨率更高的路径点。如果最后的shot trajectory存在的话，则还要加上最后一段shot trajectory(即通过computeshottraj)算出来得到的。
getSamples这一函数则是离散的获得一些轨迹点以及起始点的速度与加速度。
二、B样条曲线
首先重温一下B样条曲线的几个基本性质
1）一个有N+1个控制点的 Pb次B样条曲线，则其一共有 Pb+N+1时间节点，即 [ t 0 , t 1 , . . . t M ] 。同样的，假定希望设计一条 Pb次B样条曲线，且具备M个时间节点，则相应的控制点数量应为：M+1−Pb
2）这样一条B样条的定义域为 [tPb,tM+1−Pb]
3）每一个控制点 P i P_i Pi的作用域为[ti,ti+pb+1]
4）该B样条曲线的重的一段曲线 [ti,ti+1]只被[Pi−pb,Pi]这 pb+1个控制点影响。
2.1 均匀B样条设置
得到初始路径后，需要在前端初始路径的基础上进行B样条优化。B样条的第一部分是利用均匀B样条进行轨迹平顺性、安全性、速度和加速度优化。在non_uniform_bspline.cpp中，均匀B样条的设置函数为setUniformBspline()。这一函数在获得控制点，轨迹次数，以及时间间隔的情况下，设置时间区间（Knot vector）, 需要注意的是，在Fast-planner的实现中， tp=0, 以文章中的3次样条函数为例，t0=−3Δt, t1=−2Δt,t2=−Δt。
2.2 B样条函数值计算
给定一个时间 μ, 如何计算该点的坐标值？通常的做法是根据Cox-DeBoor公式把整个B样条函数计算出来。但在evaluateDeBoor()这一函数中，作者采用的是递归的DeBoor算法，如下图所示，具体参见wikipedia，https://en.wikipedia.org/wiki/De_Boor%27s_algorithm
其中 k 是 x落在的时间区间，即 x∈[tk,tk+1]。
假设原有与此段轨迹相关的P+1个控制点为0阶‘控制点’，通过两个循环计算出第K个P阶的‘控制点’，该点即为要求的B样条函数值。内循环通过递归公式求得高一阶的P+1个控制点，外循环提高阶数。
2.3 控制点获得-前端路径拟合
通过上面两小节，我们已经能够在已知控制点的情况下计算任一时间对应的轨迹值，那么，控制点要如何获得呢。在Fast-Planner的实现中，初始控制点时通过对前端hybrid A* 寻找到的初始路径进行拟合得到的。
虽然在计算B样条曲线上某一点的值时论文用的是DeBoor公式，但是在使用均匀B样条对前端路径进行拟合时用的是B样条的矩阵表达方法，具体参见论文：K. Qin, “General matrix representations for b-splines,” The Visual Computer, vol. 16, no. 3, pp. 177–186, 2000.
首先假设获得的离散轨迹点一共有K个，则有K-1段轨迹，根据B样条性质，这K-1段3次B样条曲线的定义域是[u3,u3+k−1]。则一共有K+5个knot vector，即 M=K−1+3+3 ，所以应该有M-3即K+2个控制点。
如以下公式所示，对于B样条曲线上定义在 tm,tm+1上的一小段曲线，其被 [pm−pb,pm]这四个控制点所决定。其中 s(t)=（t−tm）/Δt。Mpb是四维常数矩阵，具体参见以上论文链接。
通过矩阵运算，我们可以得到第一个路径点对应的位置约束：
x 1 =(Q2+4Q1+Q0)/6
同理可得其余K-1个路径点的位置约束。
对于速度约束与加速度约束，只需要对时间 t求一次及二次微分即可，所得约束关系如代码中所示。需要注意的是，由于s(t)是关于t的函数，具有常数项 1 /Δt, 所以一次及二次微分需要乘以对应的常数项 1 /Δt，1/ Δt^2。
通过对K+2个控制点构建K+4个等式约束（K个位置约束，两个速度约束，两个加速度约束），利用Ax=b Ax=b进行线性拟合，即可得到拟合的控制点。
2.4 非均匀B样条一阶及二阶微分
当我们得到一条时间节点等同的均匀B样条曲线后，我们希望能够对这条曲线上的速度及加速度进行动力学检查，以备之后进行时间节点调整。于是我们需要计算出非均匀形式下的速度控制点及加速度控制点。（直接用均匀B样条的控制点算是因为均匀B样条可以看做特殊形式的非均匀B样条）
代码中利用递归的形式求得速度与加速度，B样条的一阶微分是次数-1，控制点数-1的B样条曲线，因此相应的Knot vector-2。 在利用上图公式获得一阶微分控制点后，新定义一个NonUniformBspline对象，并将新的控制点，次数，Knot vector赋值给它。
2.5 可达性检查
这一部分的三个函数 checkFeasibility(), checkRatio(), reallocateTime()的大部分内容都是一致的。都是利用如下两个公式计算每个控制点的速度和加速度是否超限，最大速度是多少，并获得调整比例。
真正进行重新时间调整的函数时reallocateTime,通过计算当前控制点是否超限，以及调整表比例。对于当前控制点i有关的时间区间进行时间调整， [ti,ti+pb+1]。注意，这里的 pb是当前B样条的次数，如果是速度则是3-1=2, 加速度则是3-2=1（针对论文中的3次B样条曲线而言）。在 ti+pb+1以后的是时间节点则是直接加上总的扩张时间就可以。
三、B样条优化
3.1 优化项计算
利用均匀B样条进行优化，首先要看三部分的优化项及相应梯度是如何表达的。三项优化项分别是jerk平顺项，障碍物距离项，以及速度、加速度可达项。
其中，平顺项，速度、加速度项都是利用均匀B样条的微分公式，求出速度控制点，加速度控制点，jerk控制点，从而构造与相应控制点相关的优化项。梯度则是利用链式法则，用cost对影响这一cost的控制点求导，然后在循环中对cost及各控制点梯度进行累加（一个控制点会影响多个控制点的优化项）。
这里需要注意的是，速度与加速度的优化项及梯度都考虑了时间项 Δ t \Delta t Δt，但jerk项省略了时间项-或许对应文中说的后续纯几何构造法，便于后续进行时间调整。但是，平顺项的实现方式与原论文中的elastic band的方法也是不一样的。
至于障碍物项。控制点距离最近障碍物的距离及这一距离关于控制点的梯度是通过SDF地图实现的。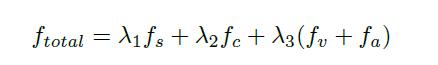
3.2 优化项结合
因为在KinoReplan中只用到Smoothness, distance，以及feasibility这三项优化项，因此，其余的优化项计算我们暂且不谈。现在考虑如何将这几项优化项结合起来，并将其自变量从控制点转化为Nlopt优化的变量x。
结合三种优化项的函数是combineCost()函数，函数有三个参数，第一个std::vector& x即是Nlopt优化的变量，应该与三个维度的控制点对应。第二个参数是std::vector& grad，即总的优化项关于每个优化变量的梯度信息。第三个参数是double& f_combine 。即结合后的Cost。
首先是给g_q赋值，g_q是用来计算每次优化循环三个优化项的控制点。值得注意的是，前 p b p_b pb个控制点和最后 p b p_b pb个控制点是不进行优化的，始终保持线性拟合得到控制点原值。中间的控制点则是因为每一次迭代优化后都不同，因此用x来赋值。这里的x是通过Nlopt的opt 对象在set_min_objective中进行初始化的，具体的大小在构造 Nlopt optimizer对象时就通过variable_num的大小确定了。而初始值则是在Nlopt求解时 .optimize函数中进行赋值。
接下来就是利用CalcSmoothneesCost, CalcDistanceCost, CalcFeasibilityCost 三个函数计算每一部分的cost和grad,并乘上权重后累加至grad 和 f_combine中，唯一需要注意的是grad和各部分优化项梯度之间维度上差了两个B样条次数。
最后，构建符合Nlopt要求的目标函数，即costFunction函数，该函数通过combinecost返回总的cost，并在参数中提供梯度信息。
3.3 Nlopt优化
至此，我们已经构造完成了优化变量、目标函数、梯度信息，接下来，我们就可以通过Nlopt对控制点进行非线性优化。
首先是BsplineOptimizeTraj()函数，将优化的控制点，均匀B样条的时间间隔，cost Function包含的优化项，以及终止条件（最大优化次数及最长优化时间）都设置好以后，就利用BsplineOptimizer的optimize()函数进行优化。
BsplineOptimizer的optimize()函数首先根据pt_num确定各部分优化项梯度vector的大小，然后再根据是否有终值点约束确定优化变量的个数。
接下来就是实例化Nlopt::opt类对象 opt。并设定目标函数。设定最大优化次数与最长优化时间，设定目标函数的最小值（这三者都是设定终止条件）。接着，根据线性你和得到的控制点设置优化变量的初值，并设置每个优化变量的上下界（初始值±10）。
最后利用Nlopt::opt类对行opt的optimize函数进行迭代优化求解，在求解结束后，通过costFunction中保留的best_Variable对control_point进行赋值。
原文链接：
blog.csdn.net/weixin_42284263/article/details/119204964
① 全网独家视频课程
BEV感知、毫米波雷达视觉融合、多传感器标定、多传感器融合、多模态3D目标检测、点云3D目标检测、目标跟踪、Occupancy、cuda与TensorRT模型部署、协同感知、语义分割、自动驾驶仿真、传感器部署、决策规划、轨迹预测等多个方向学习视频（扫码即可学习）
视频官网：www.zdjszx.com
② 国内首个自动驾驶学习社区
近2000人的交流社区，涉及30+自动驾驶技术栈学习路线，想要了解更多自动驾驶感知（2D检测、分割、2D/3D车道线、BEV感知、3D目标检测、Occupancy、多传感器融合、多传感器标定、目标跟踪、光流估计）、自动驾驶定位建图（SLAM、高精地图、局部在线地图）、自动驾驶规划控制/轨迹预测等领域技术方案、AI模型部署落地实战、行业动态、岗位发布，欢迎扫描下方二维码，加入自动驾驶之心知识星球，这是一个真正有干货的地方，与领域大佬交流入门、学习、工作、跳槽上的各类难题，日常分享论文+代码+视频，期待交流！
③【自动驾驶之心】技术交流群
自动驾驶之心是首个自动驾驶开发者社区，聚焦目标检测、语义分割、全景分割、实例分割、关键点检测、车道线、目标跟踪、3D目标检测、BEV感知、多模态感知、Occupancy、多传感器融合、transformer、大模型、点云处理、端到端自动驾驶、SLAM、光流估计、深度估计、轨迹预测、高精地图、NeRF、规划控制、模型部署落地、自动驾驶仿真测试、产品经理、硬件配置、AI求职交流等方向。扫码添加汽车人助理微信邀请入群，备注：学校/公司+方向+昵称（快速入群方式）
④【自动驾驶之心】平台矩阵，欢迎联系我们！
扫一扫
2373
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
