通俗理解齐次变换矩阵复合变换的时候变换顺序不可逆——下

为防止文章过长乏味，将此博客分为上下两篇。下篇是对上篇例题的例题常规求解和线性代数的解释。

常规求解

固连在坐标系（𝑛,𝑜,𝑎）上的点P(7,3,2)T 经历如下变换，求出变换后该点相对于固定参考坐标系的坐标。
（1）绕z轴旋转90°；
（2）接着绕y轴旋转90°；
（3）接着再平移[4,-3,7]；

倒转一下（2）和（3）的顺序
（1）绕z轴旋转90°；
（2）接着再平移[4,-3,7]；
（3）接着绕y轴旋转90°；

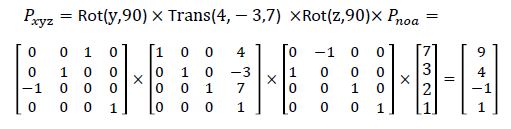
对比不同顺序的同一个步骤而言，直接看图我觉得有点抽象。大家可用自己的手臂一次平移一次旋转摆弄一下。

线性代数的解释

• 矩阵的行数和列数不允许相乘，上一个矩阵的列数不等于下一个矩阵的行数。
  如3x2的A和2x5的B可以相乘，但是BA这样的乘法是不允许的、没有定义的。
• 即使转换乘法顺序后，上一个矩阵的列数仍等于下一个矩阵的行数，得到的结果也可能不相等。
  $$A\text{A}A=\left[\begin{array}{cc}-2& 4\\ 1& -2\end{array}\right]$$

B = [ 2 4 − 3 − 6 ] \pmb{B}=\begin{bmatrix} 2 & 4 \\ -3 & -6\\ \end{bmatrix}