论文阅读——KPConv
(一)Abstract
- KPConv: 点卷积,可以在没有任何中间表示的情况下在点云上运行。
- KPConv的卷积权重: 通过kernel points位于Euclidean space中,并应用于靠近它们的输入点。其使用任意数量的kernel points的能力使KPConv比固定网格卷积更具灵活性。
- 核点位置:在空间上是连续的,并且可以由网络获知。因此,可以扩展KPConv变形卷积,学习使kernel points适应局部几何形状。
- 下采样:使KPConv在不同密度也非常有效和强大。
(二)Introduction
分析:
- 点云由两个元素组成:点 P ∈ R N × 3 P\in R^{N\times3} P∈RN×3和特征 F ∈ R N × D F\in R^{N\times D} F∈RN×D。
- 与grid不同属性:点云是一种稀疏结构,具有无序的属性。在grid中,特征通过其索引在矩阵中进行定位,而在点云中,特征通过其对应的点坐标进行定位。
- 与grid共同属性:点云在空间上是局部的(对于定义卷积至关重要)。
因而: 将点视为结构元素,将特征视为真实数据。
KPConv受基于图像的卷积的启发,但是代替核像素,使用一组kernel points 来定义每个kernel weight 的应用区域,如图1所示:
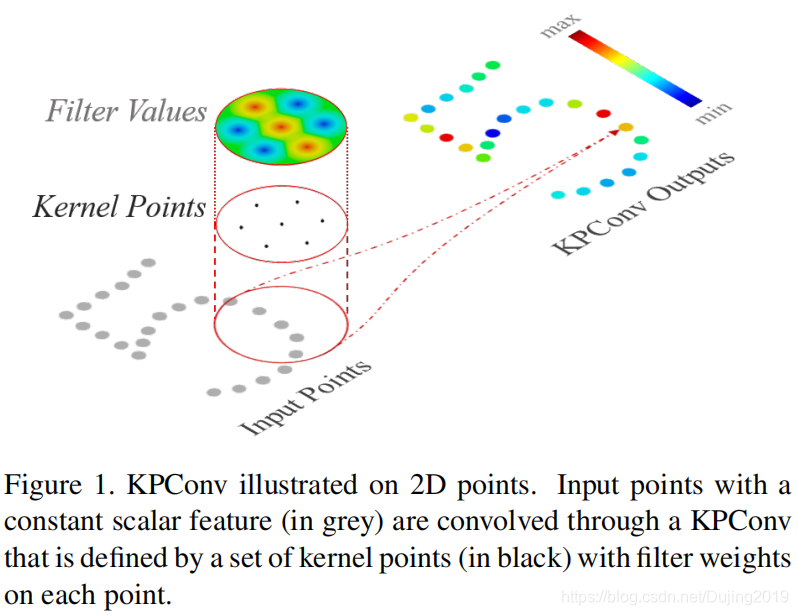
图释: The kernel weights 由点(如输入特征)承载,并且它们的影响范围由相关函数定义。 内核点数不受限制,因此设计非常灵活。
KPConv优点:

- KPConv在每个卷积位置生成不同的移位,这意味着它可以针对输入点云的不同区域调整其内核的形状。 由于数据的不同性质,需要进行正则化以帮助deformed kernels适应点云的几何形状并避免empty space。
- 倾向于使用radius neighborhoods而不是k-nearest-neighbors (KNN). 在non-uniform sampling中,KNN并不鲁棒。本文通过对radius neighborhoods和输入点云的常规下采样的组合来确保对卷积的鲁棒性。 与归一化策略相比,减轻了卷积的计算成本。
- KPConv可用于构建非常深的分类和分割网络架构,同时保持快速的训练和推理时间。
- Rigid KPConv在更简单的任务(例如对象分类或小型分割数据集)上可获得更好的性能。
- Deformable KPConv可以完成更困难的任务,例如提供许多对象实例和更大多样性的大型分割数据集。 Deformable KPConv在较少的kernel points下更强大,这意味着更大的描述能力。
- 对KPConv ERF的定性研究表明,deformable KPConv提高了网络适应场景对象的几何形状的能力。
(三)Related Work
3.1 Projection networks
多视图:
- 部分方法使用从点云在不同视点渲染的一组2D图像。 对于场景分割,这些方法受遮挡的表面和密度变化的影响。
- 部分方法建议将局部邻域投影到局部切平面,并用2D卷积对其进行处理。 但是,此方法严重依赖于切线估计。
体素:
- 将点投影到Euclidean space 中的3D网格上。 使用稀疏结构(如八叉树或哈希图)可以使用更大的网格并提高性能,但是由于kernels 被限制使用 3 3 3^3 33 = 27或 5 3 5^3 53 = 125体素,这些网络仍然缺乏灵活性。 使用permutohedral lattice代替Euclidean grid 将核减少到15个 lattices,但是这个数目仍然受到限制。
KPConv允许任何数目的kernel points。 此外,避免使用中间结构会使诸如 instance mask detector 或generative models 之类的更为复杂的体系结构的设计在以后的工作中更加直接。
3.2 Graph convolution networks
图卷积结合了局部表面patches的特征,但是对这些patches在Euclidean space中的变形是不变的。
KPConv根据3D几何形状局部组合特征,从而捕获表面的变形。
3.3 Pointwise MLP network
PointNet被认为是点云深度学习的里程碑。

继PointNet之后,一些分层体系结构将本地邻域信息与MLP聚合在一起。

3.4 Point convolution networks
点卷积的内核可以用MLP来实现,因为它具有近似任何连续函数的能力。 但是,使用这种表示方式会使卷积运算符更加复杂,并且网络的收敛也更加困难。
本文定义了一个显式卷积核,类似于图像卷积,其权重可以直接学习,而无需MLP的中间表示。 还提供了一种简单易用的deformable version,因为可以将偏移量直接应用于 kernel points。
- Pointwise CNN 使用体素容器定位内核权重,因此缺乏网格网络之类的灵活性。此外,其归一化策略使网络负担不必要的计算,而KPConv二次采样策略则减轻了密度和计算成本的变化。
- SpiderCNN 将其kernel 定义为多项式函数族,并对每个neighbor应用不同的权重。 应用于neighbor的权重取决于neighbor的距离顺序,从而使过滤器在空间上不一致。 相比之下,PConv权重位于空间中,其结果对于点顺序不变。
- Flex-convolution 使用线性函数对其内核进行建模,这可能会限制其代表性功能。 它还使用KNN,如上所述,KNN对于变化的密度并不稳健。
- PCNN 设计最接近KPConv。 其定义也使用点来承载kernel weights以及相关函数。 但是,该设计不可扩展,因为它不使用任何形式的邻域,从而使卷积计算在点数上呈二次方。 另外,它使用高斯相关,而KPConv使用更简单的线性相关,这有助于在学习 deformations 时进行梯度反向传播。
(四)Kernel Point Convolution
4.1 A Kernel Function Defined by Points
卷积核g在点 x ∈ R 3 x∈R^3 x∈R3 上对 F F F进行的一般点卷积定义为:

对于函数 g g g而言,具有一致的球形域有助于网络学习有意义的表示。 而等式1中的关键部分也是内核函数 g g g的定义,它是KPConv突出性所在。 g g g将以 x x x为中心的领域位置作为输入。在下面称它们为 y i = x i − x y_i = x_i − x yi=xi−x。
就像图像卷积内核一样(有关图像卷积和KPConv的详细比较,参见图2),希望 g g g对该球域内的不同区域应用不同的权重。
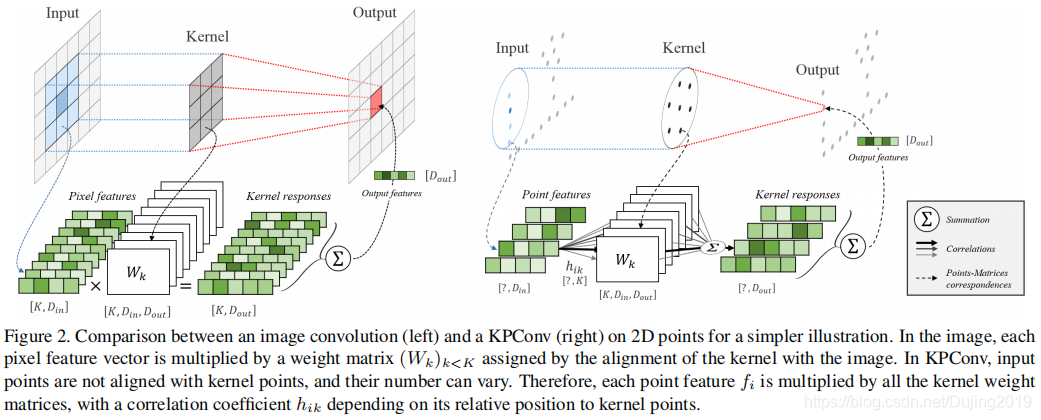
将任意点 y i ∈ B r 3 y_{i}\in B_{r}^{3} yi∈Br








 KPConv是一种适用于点云处理的灵活卷积网络,通过可变形核点适应局部几何形状。研究显示,可变形KPConv在3D场景分割等复杂任务中优于刚性KPConv,且在大型数据集上表现更佳。实验表明,即使在少量核点下,可变形KPConv仍能保持高描述能力。
KPConv是一种适用于点云处理的灵活卷积网络,通过可变形核点适应局部几何形状。研究显示,可变形KPConv在3D场景分割等复杂任务中优于刚性KPConv,且在大型数据集上表现更佳。实验表明,即使在少量核点下,可变形KPConv仍能保持高描述能力。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 808
808

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








