几何精度因子（DOP）：概念与计算方法

        几何精度因子（DOP, Dilution of Precision）是衡量卫星几何分布对 GNSS 定位精度影响的核心指标，本质是 “观测误差的放大系数”—— 卫星几何构型越优（分布均匀、覆盖广），DOP 值越小，定位误差被放大的程度越低；反之则 DOP 值越大，定位精度越差。它不直接代表定位误差，而是通过量化卫星几何质量，为定位可靠性提供判断依据。

一、DOP 的核心概念

1. 本质与作用

• 本质：由卫星与接收机的空间几何关系决定，反映 “线性观测方程中待求参数（如位置、钟差）的解算精度灵敏度”。
• 核心作用：
  1. 评估卫星组合的几何质量（DOP 越小，几何构型越优）；
  2. 关联观测误差与定位误差：定位误差 = DOP × 观测误差（如观测误差为 1m，PDOP=2，则定位误差约 2m）；
  3. 指导选星（如优先选择 DOP<3 的卫星组合）。

2. 常见 DOP 类型及含义

不同 DOP 类型对应不同定位维度的精度评估，核心类型如下表：

类型缩写	全称	评估维度	数学含义（后续计算会用到）	适用场景
GDOP	几何精度因子	3 维位置 + 接收机钟差	位置参数 + 钟差参数的精度贡献总和	需同时保证位置和时间精度（如高精度授时）
PDOP	位置精度因子	3 维位置（经度 + 纬度 + 海拔）	经度、纬度、海拔参数的精度贡献总和	3 维定位（如无人机、测绘）
HDOP	水平精度因子	水平位置（经度 + 纬度）	经度、纬度参数的精度贡献总和	车载导航（重点关注水平位置）
VDOP	垂直精度因子	垂直位置（海拔）	海拔参数的精度贡献	航空、无人机（高度精度要求高）
TDOP	时间精度因子	接收机钟差	钟差参数的精度贡献	授时场景（如 5G 基站时间同步）

二、DOP 的计算方法

DOP 的计算基于 GNSS 线性观测方程的设计矩阵（H 矩阵） 和最小二乘解的协方差矩阵，核心逻辑是：通过协方差矩阵量化待求参数的解算误差，再通过特定组合（如位置参数的误差之和开平方）得到 DOP 值。

1. 计算前提与基础公式

（1）核心输入：设计矩阵 H

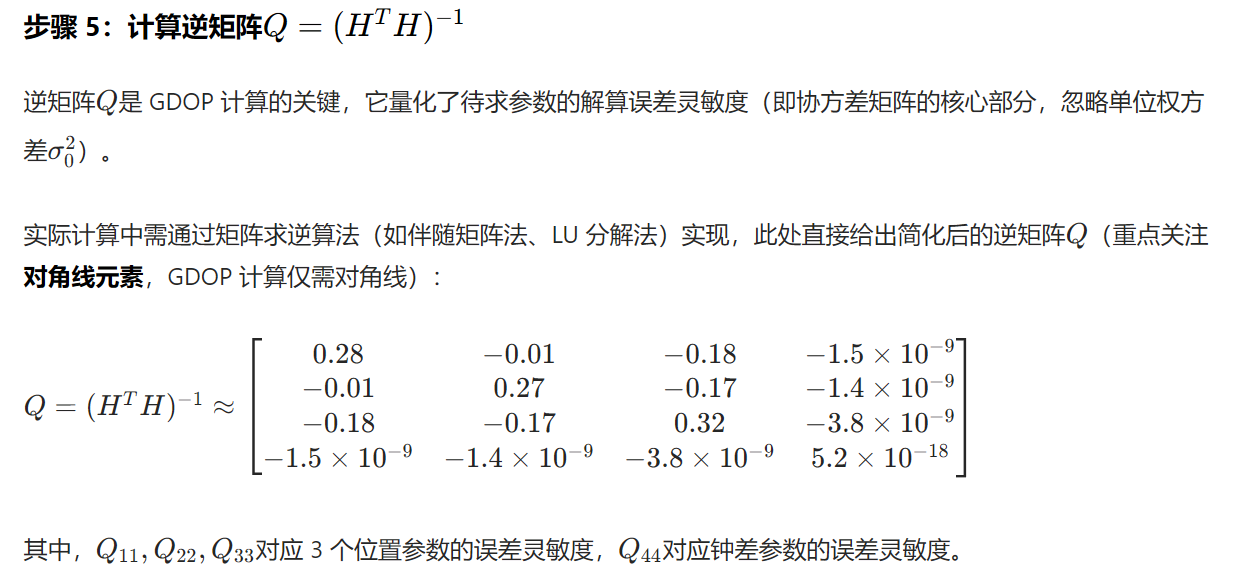
（2）最小二乘解的协方差矩阵

2. 具体 DOP 值的计算

3. 计算步骤（以 PDOP 为例）

4. 计算步骤（以 GDOP 为例）

步骤 1：准备输入数据（卫星位置与初始位置）

假设 4 颗卫星（编号 1-4）的轨道位置和接收机初始位置如下（简化数值，便于计算）：

卫星编号	卫星位置（Xi, Yi}, Zi）/m	接收机初始位置（x0, y0, z0）/m
1	(20000000, 15000000, 25000000)	(1000000, 800000, 150000)
2	(18000000, -16000000, 24000000)	(1000000, 800000, 150000)
3	(-19000000, -14000000, 23000000)	(1000000, 800000, 150000)
4	(-21000000, 17000000, 26000000)	(1000000, 800000, 150000)

同理计算 4 颗卫星的方向余弦，结果汇总（简化后）：

卫星编号	li	mi	ni
1	0.576	0.430	0.753
2	0.530	-0.495	0.727
3	-0.594	-0.438	0.697
4	-0.656	0.528	0.797

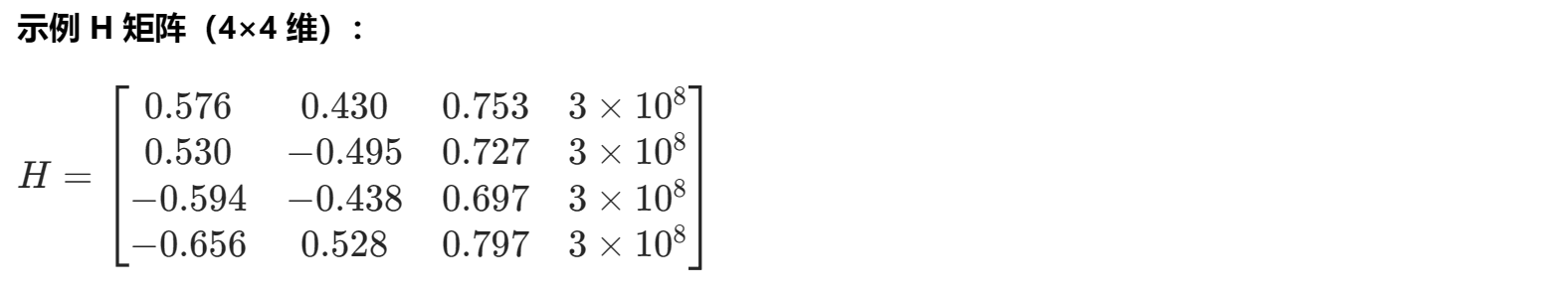
三、关键影响因素与总结

1. 核心影响因素

DOP 值完全由卫星几何分布决定，与观测误差无关：

• 卫星数量：并非越多越好，4 颗均匀分布的卫星比 10 颗集中的卫星 DOP 更小；

• 分布均匀性：卫星覆盖东、南、西、北、天顶等区域时，DOP 最小；

• 仰角：中高仰角卫星（20°-70°）为主的组合，DOP 通常优于低仰角卫星为主的组合。

2. 总结

• 概念本质：DOP 是 “卫星几何构型→参数解算误差” 的桥梁，量化误差放大程度；

• 计算核心：基于设计矩阵 H 的协方差矩阵，不同 DOP 对应参数误差的不同组合；

• 实际意义：DOP<2 为优秀，2≤DOP<3 为良好，DOP≥5 时定位精度显著下降，需重新选星。