本文围绕线性系统解的情况展开。介绍了线性系统无解和无穷解的例子，通过高斯 - 约旦消元法判断。引入行最简形式概念用于求解和判断解的结构。还从二维、三维空间直观理解线性方程组解的结构，如直线、平面相交情况对应不同解的情况。
上一部分的讨论针对的是线性系统存在n个未知数n个方程且线型系统有唯一解的情况。 但是在实际情况下， 线型系统中未知数数目和方程的数目可能并不相同，且线型系统也存在无解和无穷解的情况。这是在这一部分中着重讲解的。
无解与无穷解
线性系统无解
以下面的一个线性系统作为无解的例子引入，对于下面的线性系统依旧使用高斯-约旦消元法进行求解，
{
x
+
y
+
2
z
=
3
−
x
+
3
y
−
5
z
=
7
2
x
−
2
y
+
7
z
=
1
⟹
(
1
1
2
3
−
1
3
−
5
7
2
−
2
7
1
)
\begin{cases}x+y+2z=3\\-x+3y-5z=7\\2x-2y+7z=1\end{cases}\Longrightarrow\begin{pmatrix}1&1&2&3\\-1&3&-5&7\\2&-2&7&1\end{pmatrix}
⎩⎪⎨⎪⎧x+y+2z=3−x+3y−5z=72x−2y+7z=1⟹⎝⎛1−1213−22−57371⎠⎞
对该增广矩阵进行Gauss-Jordan消元，
⟹
(
1
1
2
3
0
4
−
3
10
0
−
4
3
−
5
)
⟹
(
1
1
2
3
0
4
−
3
10
0
0
0
5
)
\Longrightarrow\begin{pmatrix}1&1&2&3\\0&4&-3&10\\0&-4&3&-5\end{pmatrix}\Longrightarrow\begin{pmatrix}1&1&2&3\\0&4&-3&10\\{\color{red}0}&{\color{red}0}&{\color{red}0}&5\end{pmatrix}
⟹⎝⎛10014−42−33310−5⎠⎞⟹⎝⎛1001402−303105⎠⎞
未知数的系数为0，最后一行表示的是，
0
⋅
x
+
0
⋅
y
+
0
⋅
z
=
5
0\cdot x+0\cdot y+0\cdot z=5
0⋅x+0⋅y+0⋅z=5
这个等式是永远不会成立的，也就对应着线性系统无解的情况。
线性系统无穷解
下面的线性系统是一个无穷解的例子，
{
−
x
+
2
y
+
3
z
=
0
x
−
4
y
−
13
z
=
0
−
3
x
+
5
y
+
4
z
=
0
⟹
(
−
1
2
3
0
1
−
4
−
13
0
−
3
5
4
0
)
\begin{cases}-x+2y+3z=0\\x-4y-13z=0\\-3x+5y+4z=0\end{cases}\Longrightarrow\begin{pmatrix}-1&2&3&0\\1&-4&-13&0\\-3&5&4&0\end{pmatrix}
⎩⎪⎨⎪⎧−x+2y+3z=0x−4y−13z=0−3x+5y+4z=0⟹⎝⎛−11−32−453−134000⎠⎞
对增广矩阵进行Gauss-Jordan消元，
⟹
(
−
1
2
3
0
0
−
2
−
10
0
0
−
1
−
5
0
)
⟹
(
−
1
2
3
0
0
−
1
−
5
0
0
−
1
−
5
0
)
⟹
(
−
1
2
3
0
0
−
2
−
10
0
0
0
0
0
)
\Longrightarrow\begin{pmatrix}-1&2&3&0\\0&-2&-10&0\\0&-1&-5&0\end{pmatrix}\Longrightarrow\begin{pmatrix}-1&2&3&0\\0&-1&-5&0\\0&-1&-5&0\end{pmatrix}\Longrightarrow\begin{pmatrix}-1&2&3&0\\0&-2&-10&0\\0&0&0&0\end{pmatrix}
⟹⎝⎛−1002−2−13−10−5000⎠⎞⟹⎝⎛−1002−1−13−5−5000⎠⎞⟹⎝⎛−1002−203−100000⎠⎞
未知数的系数为0，最后一行表示的是，
0
⋅
x
+
0
⋅
y
+
0
⋅
z
=
0
0\cdot x+0\cdot y+0\cdot z=0
0⋅x+0⋅y+0⋅z=0
这个等式是永远成立的，也就对应着线性系统无穷解的情况。
线性系统解的判定
依据高斯消元法得到的增广矩阵结果可以判断线性系统解的数目，
行最简形式
概念
行最简形式(reduced row echelon form, RREF)，指增广矩阵按照Gauss-Jordan消元法处理后最终得到的阶梯型矩阵，该矩阵满足如下条件，
- 行第一个非0的元素（主元）为1。
- 主元所在列的其他元素均为0。
- 如果存在全部为0的行，该行必须在最下面。
以三个矩阵作为例子演示阶梯形矩阵的概念，
引入这个概念的目的是，无论是求解线性系统还是判断线性系统的解的结构都是通过RREF来判断的。
引入这个概念后即可求解更复杂的一些线型系统，RREF的形式也是多样的，下面的两个例子同样是RREF，
可以看出第一行的主元（首元）的位置不一定是在左上角的，同时增广矩阵也不要求一定是方阵。
而下面则是几个非最简形式的例子，
行最简形式与线性系统的解
由此，线性系统打破了上一节笔记中n个未知数n个方程且线性系统解唯一的形式，使得线性系统进一步复杂化。
直观理解线性方程组解的结构
二维空间引入
- 一个二元方程
一个二元方程是平面上的一条直线，直线上存在无数个点，此时线性系统有无穷解。 - 两个二元方程唯一解
方程个数：n个未知数有n个方程才可能有唯一解。以二维线性系统为例，
两个未知数两个方程存在唯一解的条件是线性空间中的两个直线存在唯一的交点。 - 两个二元方程无解
注意，n个未知数有n个方程并不是一定存在唯一解，有可能存在无解的情况，如
两个线性方程在平面中平行，即无交点，所以不存在x和y同时满足两个方程。此时，即使2个未知数有2个方程，依旧是无解的情况。 - 三个二元方程
将三个二元方程联立，在非常凑巧的情况下，三条直线能够汇聚于一点，此时线性系统存在唯一解(情况1)；
但是在大多数情况下，三条直线的情况属于第二种情况，此时方程组是无解的(情况2)；
同样的，如果三条直线恰巧重叠在一起，此时对应的是无穷解(情况3)。
三维空间拓展
- 两个三元方程的线性系统
三个未知数的线性方程是一个空间中的平面，设想如果三维空间中三个未知数存在两个方程的情况，
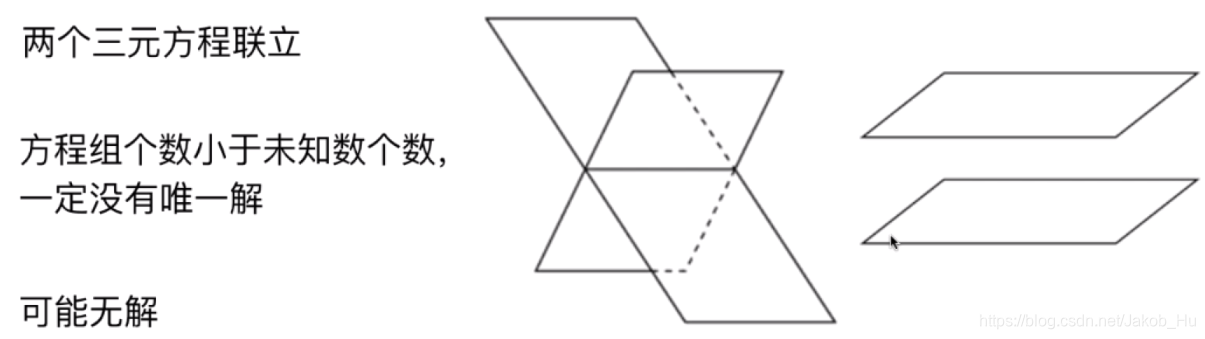
如果两个平面能相交，两个平面的相交处是一条直线，即直线上的点都满足两个平面对应的方程。但是一条直线是由无数个点构成的，这也就是方程组中方程个数小于未知数个数时一定没有唯一解的原因。如果两个平面在空间中无法相交，则对应的线性系统是无解的。 - 三个三元方程的线性系统
- 在前两个平面相交的情况下，如果第三个平面能够与这两个平面都相交且有唯一的一个交点，该点对应的三维空间中的坐标就是线性系统的唯一解。
- 如果三个平面相交在一条直线上，则依旧是一个无穷解的线性系统。
- 三个平面同样存在无解的3种情况，1）三个平面都相互平行。 2）三个平面得到两个平行线 3）三个平面两两相交得到3条平行线
- 四个三元方程组的线性系统
四个平面相交的情况可以模拟如下，
实际上是可以做到四个平面有唯一的一个交点的情况，但是在大多数的情况下，四个平面是不存在解的。这也就说明，当存在n个未知数，有多于n个线性方程时，很大概率而言，线性系统依旧是无解的。
总结
| 方程个数<未知数 | 方程个数=未知数 | 方程个数>未知数 |
|---|---|---|
| 无解 | 无解 | 无解 |
| - | 唯一解 | 唯一解 |
| 无穷解 | 无穷解 | 无穷解 |
当使用Gauss-Jordan消元法将线性系统化成行最简形式时，上面的表格会出现一些变化。系数矩阵A的非0行是不可能大于未知数个数的。也就是说下面的这种形式是不可能出现的，
(
1
0
0
c
1
0
1
0
c
2
0
0
1
c
3
0
0
0
c
4
)
\begin{pmatrix}1&0&0&c_1\\0&1&0&c_2\\0&0&1&c_3\\0&0&0&c_4\end{pmatrix}
⎝⎜⎜⎛100001000010c1c2c3c4⎠⎟⎟⎞
上面的表格可以变换为如下形式，
| 行最简形式的非零行<未知数 | 行最简形式的非零行=未知数 |
|---|---|
| 无解 | 无解 |
| - | 唯一解 |
| 无穷解 | 无穷解 |
无解的情况仅需要判断是否有行存在冲突，在没有冲突存在的情况下，这个表格可以进一步简化，
| 行最简形式的非零行<未知数 | 行最简形式的非零行=未知数 |
|---|---|
| 无穷解 | 唯一解 |
这个表格就是通过行最简形式判断的最终方法，是十分关键的。
扫一扫
1928
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
