
1.摘要
论文提出了一种基于最远点优化和多目标策略的蚁群算法,用于解决移动机器人路径规划中的问题,该算法引入了新启发式信息,如正态分布模型、三角不等式原理、平滑度函数、安全值函数等,并采用多目标综合评价指标来判断路径质量。针对高质量和低质量路径,算法通过在信息素浓度上增加或减少信息素量,加快了算法的收敛速度。此外,使用最远点优化策略进一步提升了路径质量。通过与20种现有路径规划方法进行对比实验,结果表明,该算法在收敛速度、最优路径长度和平滑度等方面表现更佳,能够在四种不同环境下生成最短路径,同时实现最少转弯,证明了改进算法的有效性。
2.基于最远点优化与多目标策略蚁群算法
初始化信息素
传统蚁群算法初始信息素设为常量,导致早期搜索盲目、收敛慢,影响全局搜索效果,论文利用正态分布模型将栅格环境划分区域,为不同区域设置信息素初值。具体做法是以起点到终点的连线作为正态分布的
y
y
y轴,并依据该模型确定各区域的初始信息素值。
y
=
a
+
b
1
2
π
σ
e
−
x
2
2
σ
2
y=a+b\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{x^2}{2\sigma^2}}
y=a+b2πσ1e−2σ2x2
改进状态转换规则
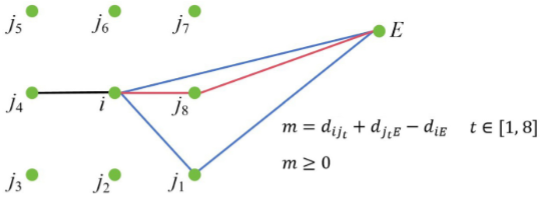
传统蚁群算法中启发式函数仅考虑当前路径点与候选路径点之间的距离,忽略了目标点的方向性,导致早期收敛性能差。为提高性能,论文引入三角不等式原理,通过计算两边之和与第三边的差值来优化启发式函数。当差值较小,路径更接近起点与终点之间的直线,从而增强目标点的方向性,提高收敛速度。同时,为避免后期过度依赖启发式函数,本文引入动态调整因子:
η
i
j
=
ψ
d
i
j
+
d
j
E
−
d
i
E
+
c
\eta_{ij}=\frac{\psi}{d_{ij}+d_{jE}-d_{iE}+c}
ηij=dij+djE−diE+cψ
平滑函数

论文在状态转移规则中引入平滑度函数,通过降低路径曲率使规划结果更加平滑,从而提升机器人的运动效率与安全性。
S
m
i
j
=
e
−
θ
2
Sm_{ij}=\mathrm{e}^{-\frac{\theta}{2}}
Smij=e−2θ
θ
=
cos
−
1
(
(
x
2
−
x
1
)
(
x
3
−
x
2
)
+
(
y
2
−
y
1
)
(
y
3
−
y
2
)
(
x
2
−
x
1
)
2
+
(
y
2
−
y
1
)
2
(
x
3
−
x
2
)
2
+
(
y
3
−
y
2
)
2
)
\theta=\cos^{-1}(\frac{(x_{2}-x_{1})(x_{3}-x_{2})+(y_{2}-y_{1})(y_{3}-y_{2})}{\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\sqrt{(x_{3}-x_{2})^{2}+(y_{3}-y_{2})^{2}}})
θ=cos−1((x2−x1)2+(y2−y1)2(x3−x2)2+(y3−y2)2(x2−x1)(x3−x2)+(y2−y1)(y3−y2))
改进后的状态转移规则:
P
i
j
k
(
t
)
=
{
[
τ
i
j
(
t
)
]
α
[
η
i
j
(
t
)
]
β
[
S
m
i
j
(
t
)
]
λ
[
S
e
j
(
t
)
]
∑
j
∈
a
l
l
o
w
e
d
k
[
τ
i
j
(
t
)
]
α
[
η
i
j
(
t
)
]
β
[
S
m
i
j
(
t
)
]
λ
[
S
e
j
(
t
)
]
j
∈
a
l
l
o
w
e
d
k
0
o
t
h
e
r
w
i
s
e
P_{ij}^{k}(t)=\begin{cases}\frac{[\tau_{ij}(t)]^{\alpha}[\eta_{ij}(t)]^{\beta}[Sm_{ij}(t)]^{\lambda}[Se_{j}(t)]}{\sum_{j\in allowed_{k}}[\tau_{ij}(t)]^{\alpha}[\eta_{ij}(t)]^{\beta}[Sm_{ij}(t)]^{\lambda}[Se_{j}(t)]}&j\in allowed_{k}\\0&otherwise&\end{cases}
Pijk(t)=⎩
⎨
⎧∑j∈allowedk[τij(t)]α[ηij(t)]β[Smij(t)]λ[Sej(t)][τij(t)]α[ηij(t)]β[Smij(t)]λ[Sej(t)]0j∈allowedkotherwise
改进信息素更新规则
论文引入多目标综合评价指标用于衡量路径质量,并对高质量与低质量路径分别采取不同的信息素增减策略,从而强化优质路径、削弱劣质路径,加速算法收敛并提升全局搜索性能。
τ i j ( t + 1 ) = ( 1 − ρ ) τ i j ( t ) + Δ τ i j ( t ) + Δ τ i j b e s t − Δ τ i j w o r s t \tau_{ij}(t+1)=(1-\rho)\tau_{ij}(t)+\Delta\tau_{ij}(t)+\Delta\tau_{ij}^{best}-\Delta\tau_{ij}^{worst} τij(t+1)=(1−ρ)τij(t)+Δτij(t)+Δτijbest−Δτijworst
Δ
τ
i
j
b
e
s
t
=
{
ρ
×
Q
×
(
σ
1
J
m
i
n
+
σ
2
J
m
a
x
)
J
m
i
n
i
,
j
∈
B
e
s
t
J
0
o
t
h
e
r
w
i
s
e
\Delta\tau_{ij}^{best}=\left\{\begin{array}{cc}{\frac{\rho\times Q\times(\sigma_{1}J_{min}+\sigma_{2}J_{max})}{J_{min}}}&{i,j\in BestJ}\\{0}&{otherwise}\end{array}\right.
Δτijbest={Jminρ×Q×(σ1Jmin+σ2Jmax)0i,j∈BestJotherwise
Δ
τ
i
j
w
o
r
s
t
=
{
ρ
×
Q
J
m
a
x
i
,
j
∈
W
o
r
s
t
J
0
o
t
h
e
r
w
i
s
e
\Delta\tau_{ij}^{worst}=\left\{\begin{array}{cc}\frac{\rho\times Q}{J_{max}}&i,j\in WorstJ\\0&otherwise\end{array}\right.
Δτijworst={Jmaxρ×Q0i,j∈WorstJotherwise
最远点优化
论文用最远点优化方法对机器人路径进行二次优化,通过去除冗余节点和不必要的转弯,减少路径长度。优化过程从起始节点出发,比较直线距离与原路径长度,选择更短的路径并删除中间节点,最终得到平滑的路径,显著降低了路径长度、机器人运行时间和能耗。

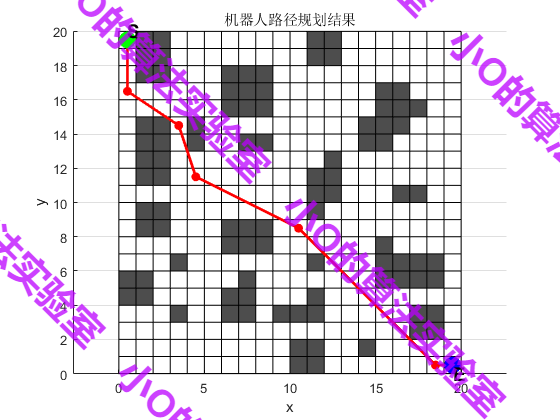
3.结果展示
4.参考文献
[1] Wu S, Dong A, Li Q, et al. Application of ant colony optimization algorithm based on farthest point optimization and multi-objective strategy in robot path planning[J]. Applied Soft Computing, 2024, 167: 112433.
5.代码获取
xx
6.算法辅导·应用定制·读者交流
xx



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










