二、导航基础知识
在了解惯导解算及多传感器组合导航之前,肯定要先掌握导航基础知识:如矩阵基础知识、欧拉角、坐标转换矩阵、四元数、等效旋转矢量、地球模型、重力模型等等
矩阵基础知识
1、向量叉乘与反对称阵
两个三维列向量
V
1
=
[
V
1
x
,
V
1
y
,
V
1
z
]
,
V
2
=
[
V
2
x
,
V
2
y
,
V
2
z
]
V_1=[V_{1x},V_{1y},V_{1z}],V_2=[V_{2x},V_{2y},V_{2z}]
V1=[V1x,V1y,V1z],V2=[V2x,V2y,V2z]之间的叉乘(外积),可利用行列式计算规则表示为:

其中i,j,k分别为直角坐标系三个坐标轴向的单位向量。
上式等于:

因此可记:

可知,
(
V
×
)
(V\times)
(V×)是反对称阵,当V是实向量时满足:
(
V
×
)
H
=
(
V
×
)
T
=
−
(
V
×
)
(V\times)^H=(V\times)^T=-(V\times)
(V×)H=(V×)T=−(V×)(其中H代表共轭转置)。后面将
(
V
×
)
(V\times)
(V×)记为由三维向量V构成的反对称阵。引入三维向量的反对称阵概念后,两向量之间的叉乘运算可等价表示为前一向量的反对称阵与后一向量之间的矩阵乘法运算,亦即
V
1
×
V_1\times
V1×
V
2
=
(
V
1
×
)
V
2
V_2=(V_1\times)V_2
V2=(V1×)V2。且反对称阵
(
V
×
)
(V\times)
(V×)是正规矩阵
(
V
×
)
H
(V\times)^H
(V×)H
(
V
×
)
=
(V\times)=
(V×)=
(
V
×
)
(V\times)
(V×)
(
V
×
)
H
(V\times)^H
(V×)H。
欧拉角、坐标转换矩阵、四元数、等效旋转矢量
1、欧拉角
三维空间的物体具有六个自由度,绕XYZ轴的平移以及绕XYZ轴的旋转,所以,旋转是具有三个自由度的,惯导中,一般用yaw(偏航), pitch(俯仰), roll(横滚)三个量表示,一般对应(载体)z,y,x(前-右-下坐标系)三个坐标轴(若为右-前-上坐标系则为z,x,y)。
要清楚描述旋转,则必须明确旋转顺序与内旋还是外旋。
1、旋转顺序
旋转顺序如先X-Y-Z或先Y-X-Z等, (x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z)。
对于x,y,z三个轴的不同旋转顺序一共有(x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z)六种组合,而旋转具有不可交换性,即先绕Z轴转30度,再绕Y轴转10度,最后绕X轴转40度,先绕Y轴转10度,再绕Z轴转30度,最后绕X轴转40度得到的结果是不同的,因此我们需要明确旋转顺序,才能确定欧拉角所指的姿态。
2、内旋与外旋
内旋= 绕自身旋转轴(惯导解算采用的就是内旋)
外旋= 绕世界坐标系固定的旋转轴
如下图所示,两行都是按照Z-Y顺序旋转,不同的是上面一行的第二次旋转是按照旋转之后的Y轴旋转,而下面一行是按照绕Z轴旋转之前的Y轴进行的旋转,所以,上面一行的旋转被称为内旋(按照坐标系自己的轴向旋转),而下面则被称为外旋(按照参考坐标系的轴向旋转)。

注意,导航中,我们常常会看到,导航系或当地地理坐标系到载体系的坐标旋转矩阵,绕Y轴旋转时,其与绕X、Z轴的写法不一致(可参考我上一篇文章),是因为绕X、Z轴旋转时,对应的分别是(在yoz、xoy平⾯顺时针旋转),然而绕Y轴旋转时,对应的是在zox平面顺时针旋转(z轴此时是横轴,x是纵轴),因此绕Y轴的坐标转换矩阵与绕其他轴不一样,这个也可以通过右手坐标系比划一下得出~~。
欧拉角的缺点及优点:
优点:旋转三个自由度正好通过三个变量表示出来,无冗余,且直观
缺点:存在万向节死锁问题、没办法进行旋转的叠加,必须借助旋转矩阵、插值误差大,因为是三个轴进行的旋转。但是四元数就十分适合插值。
万向节死锁简易解释:y向上,x向右,z向屏幕里面。假设应用顺序为x->y->z,如果我想转一个(10,90,20),那么我先在x上面转10度,然后,y转90度,此时,z轴指向了y旋转前x的方向的反方向,所以,第三步,在z上转20度,可以直接减在第一步里,在x上转-10度,因此,可以认为此时在z轴向上应用任何旋转是没有意义的,即丢失了一个自由度。
我们从最简单的矩阵来理解。还是使用XYZ的旋转顺序。当Y轴的旋转角度为90°时,我们会得到下面的旋转矩阵:
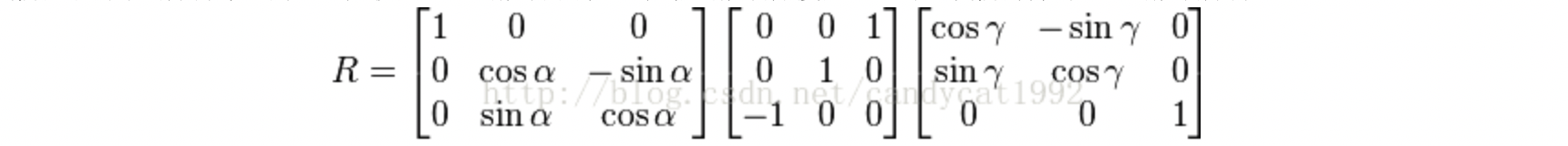
我们对上述矩阵进行左乘可以得到下面的结果:

可以发现,此时当我们改变第一次和第三次的旋转角度时,是同样的效果,而不会改变第一行和第三列的任何数值,从而缺失了一个维度。
2、坐标转换矩阵
用一个3阶正交矩阵来表示旋转变换,是一种最常用的表示方法。容易证明,3阶正交阵的自由度为3。注意,它的行列式必须等于1。
坐标转换矩阵相对于欧拉角来说更适合运算,两次连续旋转可用坐标转换矩阵相乘来表达。
坐标转换矩阵的缺点及优点:
优点:相比于欧拉角的多样性,同一个姿态的旋转矩阵是唯一的、可以直接做旋转的相乘运算、相比于四元数,对坐标转化更加友好。
缺点:用9个量表示三个自由度,冗余度太大了。
3、四元数
欧拉角存在万向锁,旋转矩阵冗余度太大,所以引入四元数,即一次转动可以由四个元素组成的超复数组成:
q
=
(
q
0
,
q
1
,
q
2
,
q
3
)
q=(q_0,q_1,q_2,q_3)
q=(q0,q1,q2,q3),其中
q
0
q_0
q0为转动幅度的函数,
q
1
,
q
2
,
q
3
q_1,q_2,q_3
q1,q2,q3为转动轴、转动幅度的函数,因为旋转自由度为3,尽管四元数有四个量,但是其模值为1,因此四元数也只有三个量是“自由”相互独立的。
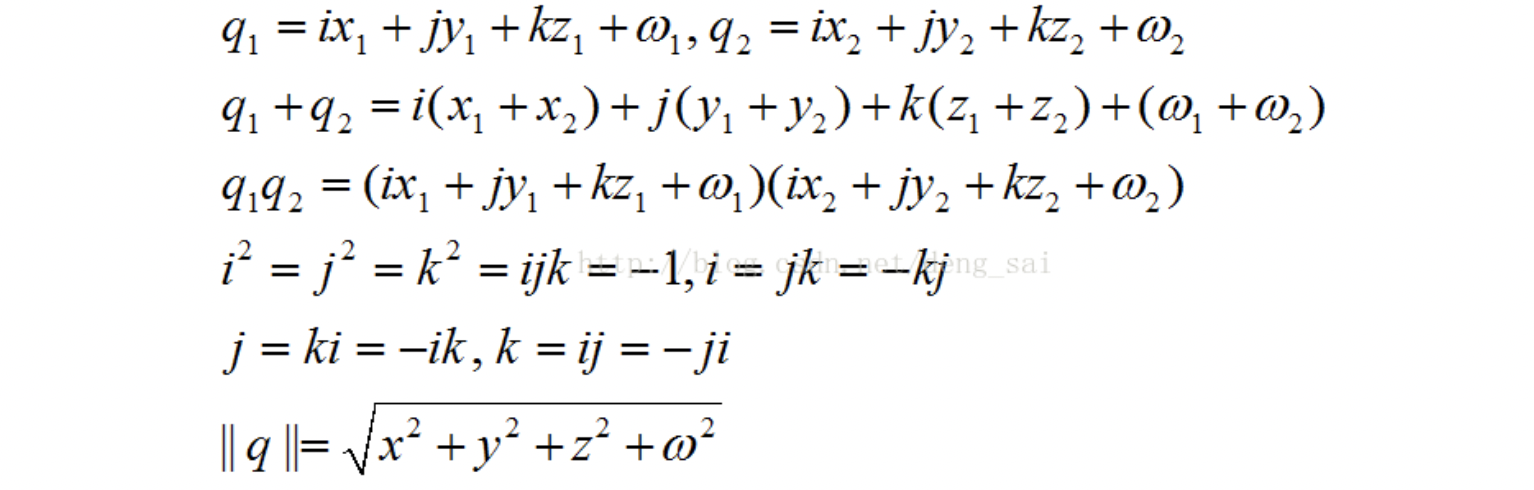

其中
q
∗
q^*
q∗是
q
q
q的共轭,
q
∗
v
∗
q
∗
q*v*q^*
q∗v∗q∗就是三个四元数连乘,可以理解为
v
v
v被
q
q
q和
q
∗
q^*
q∗各旋转了一次。如果我们就想旋转θ角度,那旋转一次行不行呢?不行!,旋转后的v′的实部不为零,用下面的图来表示:
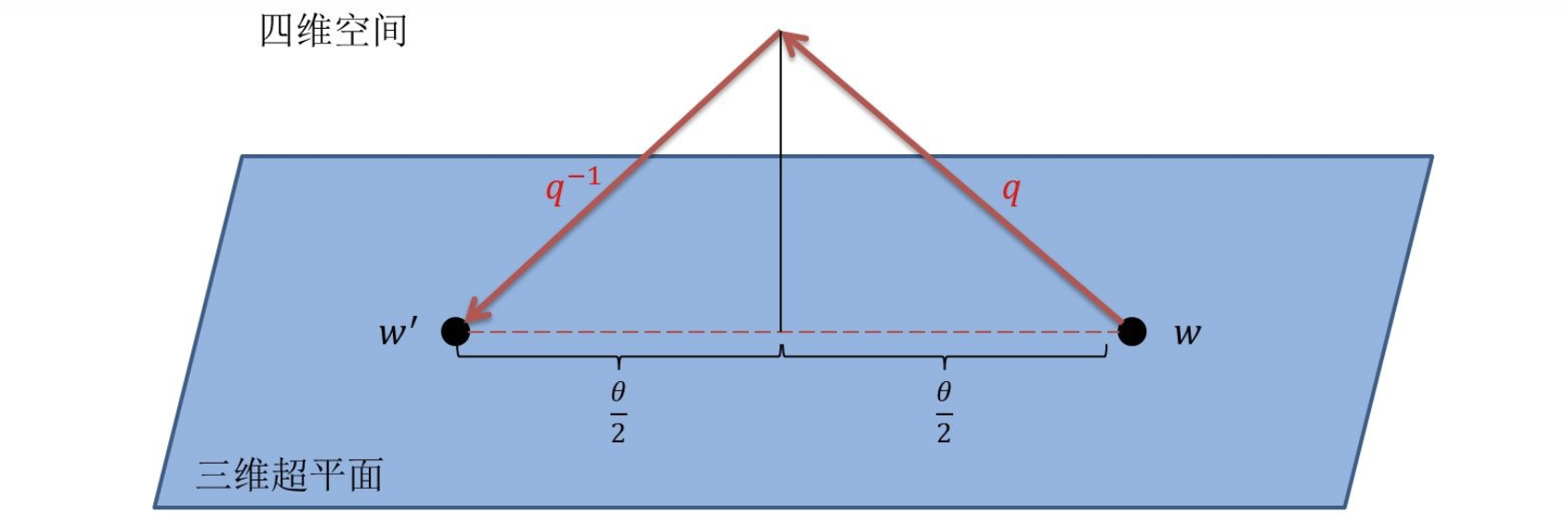
上图的三维超平面代表三维世界(i,j,k),三维向量w在三维超平面上,所以第四维度的大小为0,w在四维空间上表示为[0,b,c,d],如果被四元数
q
q
q旋转一次,w就变成了箭头指向上方的点,这个点是三维超平面上,这时的第四维度的大小不为零了。w在四维空间上表示为[a,b,c,d],三维向量被转化为四维向量。这就很尴尬了!!!如果再继续被
q
∗
q^*
q∗ 旋转一次,恰好就又被转化到三维超平面之上了。
由于四元数原理推导及理论有些复杂,篇幅限制,不在这里详细介绍,如果对四元数不是很熟的同学,可以看一下Krasjet大神写的四元数与三维旋转这个文章,介绍的非常非常详细,链接如下:最详细的四元数讲解,保姆级教学
4、轴角/旋转矢量
在轴角的表示方法中,一个旋转的定义需要使用到四个变量:旋转轴 u 的 𝑥, 𝑦, 𝑧 坐标,以及一个旋转角 θ,也就是我们一共有四个自由度 (Degree of Freedom).这很明显是多于欧拉角的三个自由度的.实际上,任何三维中的旋 转只需要三个自由度就可以定义了,为什么这里我们会多出一个自由度呢?

其实,在我们定义旋转轴 u 的 𝑥, 𝑦, 𝑧 坐标的同时,我们就定义了 u 的模 长(长度).然而,通常情况下,如果我们说绕着一个向量 u 旋转,我们其实 指的是绕着 u 所指的方向进行旋转.回忆一下向量的定义:向量是同时具有 大小和方向的量,但是在这里它的大小(长度)并不重要.我们可以说绕着 u1 = (0, 0, 1)𝑇 这个轴进行旋转,也可以说绕着 u2 = (0, 0, 3)𝑇 旋转.虽然这 两个向量完全不同,但是它们指向的都是同一个方向(即 𝑧 轴的方向)。在三维空间中定义一个方向只需要用到两个量就可以了(与任意两个坐标 轴之间的夹角).最简单的例子就是地球的经纬度,我们仅仅使用经度和纬 度两个自由度就可以定义地球上任意一个方位.而如果我们要表示某一个方 位上的特定一个点,则还需要添加海拔这个自由度。为了消除旋转轴 u 模长这个多余的自由度,我们可以规定旋转轴 u 的模长 为
∣
∣
u
∣
∣
=
s
q
r
t
(
x
2
+
y
2
+
z
2
)
=
1
||u||=sqrt(x^2+y^2+z^2)=1
∣∣u∣∣=sqrt(x2+y2+z2)=1,也就是说 u 是一个单位向量.这样一来,空间中任意一个方向上的单位向量就唯一代表了这个方向。
轴角和旋转向量本质上是一个东西,轴角用四个元素表达旋转,其中的三个元素用来描述旋转轴,另外一个元素描述旋转的角度:
r
=
[
x
,
y
,
z
,
θ
]
r=[x,y,z,\theta]
r=[x,y,z,θ] ,其中单位向量
n
=
[
x
,
y
,
z
]
n=[x,y,z]
n=[x,y,z]对应的是旋转轴,
θ
\theta
θ对应的是旋转角度。旋转向量与轴角相同,只是旋转向量用三个元素来描述旋转,它把
θ
\theta
θ角乘到了旋转轴上,如下:
r
v
=
[
x
∗
θ
,
y
∗
θ
,
z
∗
θ
]
r_v=[x*\theta,y*\theta,z*\theta]
rv=[x∗θ,y∗θ,z∗θ]。
有了这个约束,我们现在就可以开始思考怎么样进行这个旋转了.首先, 我们可以将 v 分解为平行于旋转轴 u 以及正交(垂直)于 u 的两个分量,
v
∥
v_∥
v∥ 和
v
⊥
v_⊥
v⊥,即

我们可以分别旋转这两个分向量,再将它们旋转的结果相加获得旋转后的向量


可以看到,
v
∥
v_∥
v∥ 其实就是 v 在 u 上的正交投影 ,根据正交投影的公式,我们可以得出:

因为
v
=
v
∥
+
v
⊥
v = v_∥ + v_⊥
v=v∥+v⊥,我们可以得到
v
⊥
=
v
−
v
∥
=
v
−
(
u
⋅
v
)
u
.
v_⊥ = v − v_∥ = v − (u · v)u.
v⊥=v−v∥=v−(u⋅v)u. 因此,v的旋转被分解成了
v
∥
v_∥
v∥ 以及
v
⊥
v_⊥
v⊥的旋转。而
v
∥
v_∥
v∥ 其实根本就没有被旋转,仍然与旋转轴 u 重合,因此
v
∥
′
=
v
∥
v ^′_∥ = v ∥
v∥′=v∥
接下来,我们需要处理正交于 u 的
v
⊥
v_⊥
v⊥,因为这两个向量是正交的,这个旋转可以看做是平面内的一个旋转.因为旋转不改变
v
⊥
v_⊥
v⊥ 的长度,所以路径是 一个圆.下面是这个旋转的示意图,右侧的为俯视图:

现在,3D 的旋转就被我们转化为了 2D 平面上的旋转.由于在这个平面上我们只有一个向量
v
⊥
v_⊥
v⊥,用它来表示一个旋转是不够的,我们还需要构造一个同时正交于 u 和
v
⊥
v_⊥
v⊥ 的向量 w,这个可以通过叉乘来获得:
w
=
u
×
v
⊥
w=u×v_⊥
w=u×v⊥。w 指向
v
⊥
v_⊥
v⊥逆时针旋转 𝜋/2 后的方向,并且和
v
⊥
v_⊥
v⊥一样也处于正交于u的平面内.因为
∥
u
∥
=
1
∥u∥ = 1
∥u∥=1,我们可以发现

我们现在可以把
v
⊥
′
v^′_⊥
v⊥′ 投影到w和
v
⊥
v_⊥
v⊥上,将其分解为
v
𝑣
′
v^′_𝑣
vv′ 和
v
𝑤
′
v^′_𝑤
vw′有:
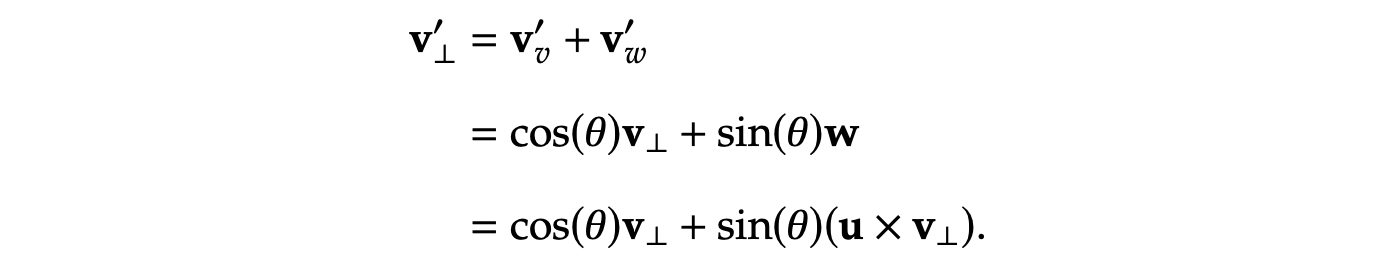
将上面的两个结果组合就可以获得:

因为叉乘遵守分配律:

最后,将
v
∥
=
(
u
⋅
v
)
u
与
v
⊥
=
v
−
(
u
⋅
v
)
u
v_∥ =(u·v)u与v_⊥ =v−(u·v)u
v∥=(u⋅v)u与v⊥=v−(u⋅v)u代入:
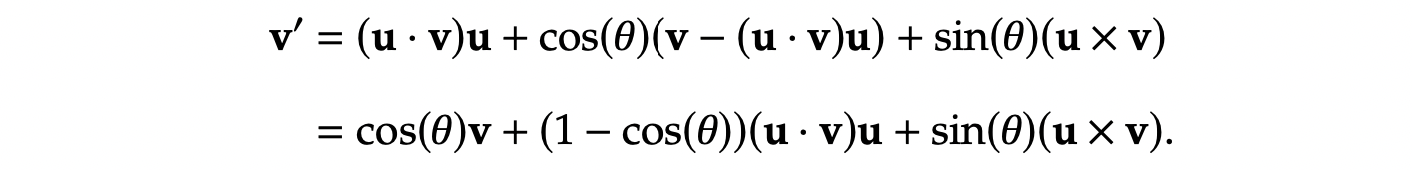
上述公式就是一般形式的旋转公式。
5、欧拉角、坐标转换矩阵、四元数、等效旋转矢量间相互转换
1、欧拉角<=>坐标转换矩阵
假设坐标系1的欧拉角yaw、pitch、roll的角度为
α
,
β
,
γ
α,β,γ
α,β,γ,可以由公式:
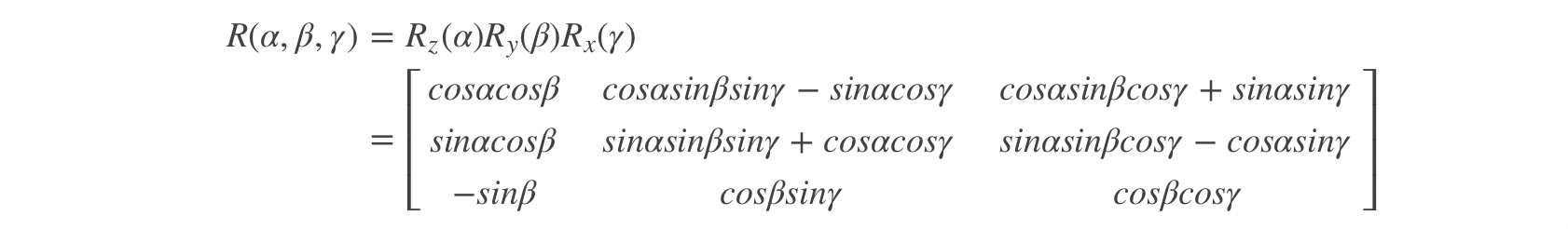
其中:
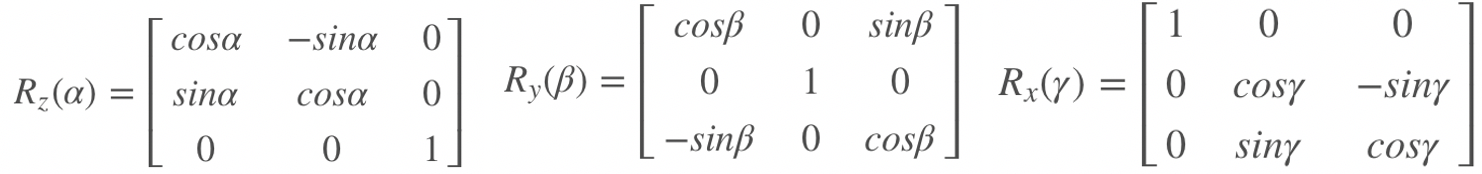
其实上式就是北东地坐标系下的姿态矩阵的写法。则坐标转换矩阵转欧拉角如下:

2、欧拉角<=>四元数
若绕z-y-x轴的顺序旋转,欧拉角为yaw (ψ), pitch (θ) and roll (φ) :

反过来
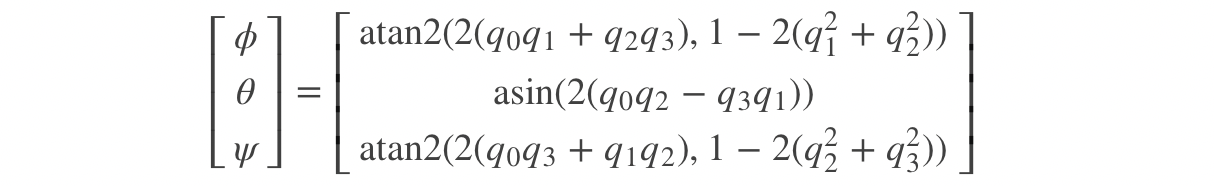
3、坐标转换矩阵<=>四元数
在实际的应用中,我们可能会需要将旋转与平移和缩放进行复合,所以需 要用到四元数旋转的矩阵形式.它可以很容易地从上面这个公式推导出来. 我们之前讨论过,左乘一个四元数 𝑞 = 𝑎 + 𝑏𝑖 + 𝑐𝑗 + 𝑑𝑘 等同于下面这个矩阵

而右乘 𝑞 等同于这个矩阵:

定义为纯四元数
𝑣
=
[
0
,
v
]
𝑣 = [0, v]
v=[0,v],上面已经得知

假设
𝑎
=
c
o
s
1
2
θ
𝑎=cos\frac {1} {2}θ
a=cos21θ,
𝑏
=
s
i
n
1
2
θ
𝑢
𝑥
,
𝑐
=
s
i
n
1
2
θ
𝑢
𝑦
,
𝑑
=
s
i
n
1
2
θ
𝑢
𝑧
,
𝑞
=
𝑎
+
𝑏
𝑖
+
𝑐
𝑗
+
𝑑
𝑘
𝑏=sin \frac {1} {2}θ 𝑢_𝑥,𝑐=sin \frac {1} {2}θ 𝑢_𝑦,𝑑=sin\frac {1} {2}θ 𝑢_𝑧,𝑞=𝑎+𝑏𝑖+𝑐𝑗+𝑑𝑘
b=sin21θux,c=sin21θuy,d=sin21θuz,q=a+bi+cj+dk,我们就能得到:

因为
𝑎
2
+
𝑏
2
+
𝑐
2
+
𝑑
2
=
1
𝑎_2 +𝑏_2 +𝑐_2 +𝑑_2 =1
a2+b2+c2+d2=1,这个式子能化简为:
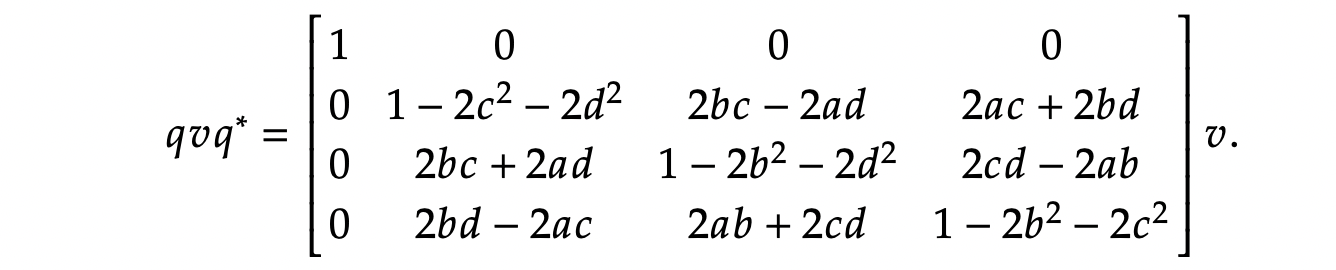
这样我们就得到了 3D 旋转的矩阵形式.因为矩阵的最外圈不会对 𝑣 进行任 何变换,我们可以将它压缩成 3 × 3 矩阵(用作 3D 向量的变换):任意向量 v 沿着以单位向量定义的旋转轴 u 旋转 θ 角度之后的 v′ 可以使用矩阵乘法来获得.令
𝑎
=
c
o
s
1
2
θ
𝑎=cos\frac {1} {2}θ
a=cos21θ,
𝑏
=
s
i
n
1
2
θ
𝑢
𝑥
,
𝑐
=
s
i
n
1
2
θ
𝑢
𝑦
,
𝑑
=
s
i
n
1
2
θ
𝑢
𝑧
,
𝑏=sin \frac {1} {2}θ 𝑢_𝑥,𝑐=sin \frac {1} {2}θ 𝑢_𝑦,𝑑=sin\frac {1} {2}θ 𝑢_𝑧,
b=sin21θux,c=sin21θuy,d=sin21θuz, 那么:
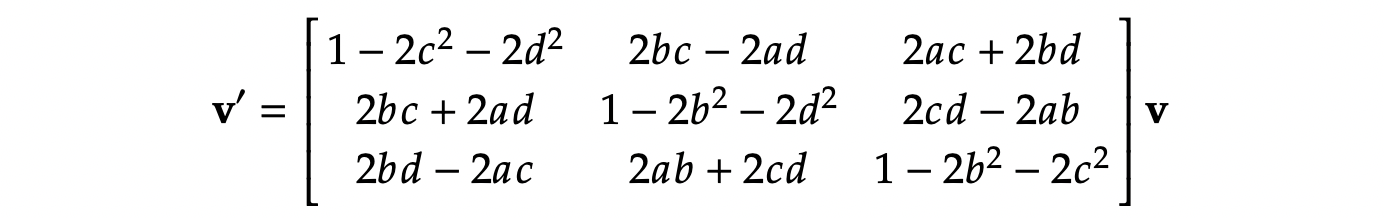
这个也等同于:

坐标转换矩阵转四元数:

4、坐标转换矩阵<=>旋转向量
当刚体在三维空间中运动时,如果已知旋转向量,根据罗德里格斯公式是比较容易求得旋转矩阵的:
将旋转向量转换为旋转矩阵:

将旋转矩阵转换为旋转向量:
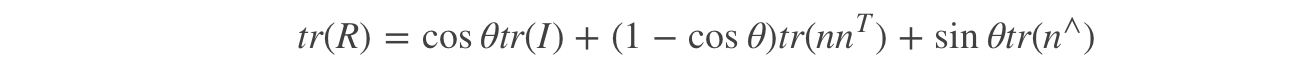
θ
=
a
r
c
c
o
s
(
t
r
(
R
)
−
1
2
)
\theta=arccos(\frac {tr(R)-1} {2})
θ=arccos(2tr(R)−1)
5、四元数<=>旋转向量
四元数转旋转矩阵:
θ
=
2
a
r
c
c
o
s
(
q
0
)
\theta=2arccos(q_0)
θ=2arccos(q0),
[
n
x
,
n
y
,
n
z
]
T
=
[
q
1
,
q
2
,
q
3
]
T
/
s
i
n
θ
2
[n_x,n_y,n_z]^T=[q_1,q_2,q_3]^T/sin\frac {\theta} {2}
[nx,ny,nz]T=[q1,q2,q3]T/sin2θ
旋转矩阵转四元数:
q
=
[
c
o
s
θ
2
,
s
i
n
θ
2
n
x
,
s
i
n
θ
2
n
y
,
s
i
n
θ
2
n
z
]
q=[cos\frac {\theta} {2},sin\frac {\theta} {2} n_x,sin\frac {\theta} {2} n_y,sin\frac {\theta} {2} n_z]
q=[cos2θ,sin2θnx,sin2θny,sin2θnz]
地球形状及重力模型
1、地球形状
1、地心纬度与地理纬度
椭圆上任一点
P
P
P与
P
o
e
Po_e
Poe地心连线与
o
e
x
e
o_ex_e
oexe轴的夹角称为地心纬度,记为
φ
\varphi
φ,取值范围为−90°~90°,南纬为负而北纬为正。过
P
P
P点的椭圆法线
P
Q
PQ
PQ与
o
e
x
e
o_ex_e
oexe轴的夹角称为地理纬度(简称纬度,latitude),符号记为
L
L
L,取值范围为−90°~90°。此外,
P
o
e
Po_e
Poe与地心纬度对应的方向 称为地心垂线,而与地理纬度对应的方向
P
Q
PQ
PQ称为地理垂线。

R
e
R_e
Re和
R
n
R_n
Rn分别为椭圆长半轴和短半轴,则:
椭圆扁率(或称椭圆度,flattening)定义为:

椭圆偏心率(eccentricity)定义为:
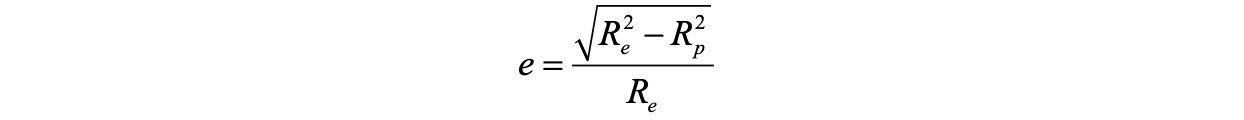
可得
f
f
f与
e
e
e之间的相互换算关系:

2、大地坐标与位置矩阵
在旋转椭球表面上
P
P
P点处,纬圈切线与经圈切线相互垂直,且两切线同时垂直于椭球面的法线。在椭球表面上定义直角坐标系
o
0
x
0
y
0
z
0
o_0x_0y_0z_0
o0x0y0z0:
P
P
P点为坐标原点(重记为
o
0
o_0
o0),纬圈切线指东、经圈切线指北、椭球面法线指天分别为
o
0
x
0
o_0x_0
o0x0轴、
o
0
y
0
o_0y_0
o0y0轴和
o
0
z
0
o_0z_0
o0z0轴的正向。若某点
o
g
o_g
og在坐标系
o
0
x
0
y
0
z
0
o_0x_0y_0z_0
o0x0y0z0中的直角坐标为
o
g
(
0
,
0
,
h
)
o_g(0,0,h)
og(0,0,h),显然
o
g
o_g
og在椭球面
P
P
P点的法线上,
h
h
h称为
o
g
o_g
og点的椭球高度,简称椭球高。以
o
g
o_g
og为原点建立坐标系
o
g
x
g
y
g
z
g
o_gx_gy_gz_g
ogxgygzg,其三轴分别平行于
o
0
x
0
y
0
z
0
o_0x_0y_0z_0
o0x0y0z0的同名坐标轴,称
o
g
x
g
y
g
z
g
o_gx_gy_gz_g
ogxgygzg为当地地理坐标系,简记为g系。
o
g
o_g
og点相对于地球椭球的空间位置可用所谓的大地坐标(地理坐标)表示,记为
o
g
(
λ
,
L
,
h
)
o_g(\lambda,L,h)
og(λ,L,h) 。

在上图中,如果
o
0
o_0
o0点相对地球坐标系
o
e
x
e
y
e
z
e
o_ex_ey_ez_e
oexeyeze的速度在
o
0
x
0
y
0
z
0
o_0x_0y_0z_0
o0x0y0z0系的投影记为
v
e
o
0
v
o
0
=
[
v
x
0
,
v
y
0
,
0
]
T
v_{eo_0}^{vo_0}=[v_{x_0},v_{y_0},0]^T
veo0vo0=[vx0,vy0,0]T。注意到
o
0
x
0
o_0x_0
o0x0轴与纬圈相切,两者在同一个平面内,因此
v
x
0
v_{x_0}
vx0仅会引起经度的变化,有

同理,
o
0
y
0
o_0y_0
o0y0轴与经圈相切,两者在同一平面内,因而速度
v
y
0
v_{y_0}
vy0仅会引起纬度的变化,考虑到
P
P
P点所在子午圈的曲率半径为
R
M
R_M
RM,则有

对于高度为
h
h
h的
o
g
o_g
og点,假设其速度为
v
e
g
g
=
[
v
x
,
v
y
,
v
z
]
T
v_{e_g}^{g}=[v_{x},v_{y},v_{z}]^T
vegg=[vx,vy,vz]T,有:

并考虑到天向速度
v
z
v_z
vz仅引起高度
h
h
h的变化,得到速度
v
e
g
g
v_{e_g}^{g}
vegg与大地坐标
(
λ
,
L
,
h
)
(\lambda,L,h)
(λ,L,h) 之间的关系,分别为:

当然,这里使用的是东北天坐标系,即
v
x
v_x
vx代表东向速度,
v
y
v_y
vy代表北向速度,
v
z
v_z
vz代表天向速度。如果是北东地坐标系,则
v
x
v_x
vx、
v
y
v_y
vy要反过来,地向速度前面加负号。
2、重力模型
重力是地球万有引力和离心力共同作用的结果,参见下图,在
P
P
P点处,重力矢量
g
g
g是引力矢量
F
F
F和离心力矢量
F
′
F'
F′的合力。

若将地球视为圆球体并且认为密度均匀分布,那么地球引力指向地心,根据牛顿万有引力定律,地球对其表面或外部单位质点的引力大小为

其中,G为万有引力常数;M为地球质量,r为质点至地心的距离。
由于地球绕其极轴存在自转角速率,使得与地球表面固连的单位质点受到离心力的作用,其大小为

其中,R为圆球半径;L为地理纬度(在圆球假设中即为地心纬度)
重力是引力与离心力的合力,引力与离心力之间的夹角为pi-L,根据余弦定理,在纬度为L处P点的重力大小为

其中,
g
e
=
F
−
w
i
e
2
R
g_e=F-w_{ie}^2R
ge=F−wie2R为赤道上的重力大小;
实测表明,基于圆球假设的重力公式与实际椭球地球相比精度不足,旋转椭球假设下的地球重力为:

总算整理完这个了,累懵逼了都QAQ








 本文详细介绍了导航中的矩阵基础知识,包括向量叉乘与反对称阵,以及欧拉角、坐标转换矩阵、四元数和等效旋转矢量的概念和相互转换。欧拉角存在万向节死锁问题,而四元数和坐标转换矩阵作为替代方案各有优缺点。此外,还探讨了地球形状、地心纬度、重力模型等相关知识。
本文详细介绍了导航中的矩阵基础知识,包括向量叉乘与反对称阵,以及欧拉角、坐标转换矩阵、四元数和等效旋转矢量的概念和相互转换。欧拉角存在万向节死锁问题,而四元数和坐标转换矩阵作为替代方案各有优缺点。此外,还探讨了地球形状、地心纬度、重力模型等相关知识。
















 272
272

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








