【模拟带有优化的连续死区控制】基于粒子群优化算法的非最小相位系统的最小化欠阻尼研究（Matlab代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、数据、文章

---

💥1 概述

这篇论文处理了在连续死区条件下非最小相位系统的跟踪性能。众所周知，对于带有不稳定零点的系统，跟踪性能受到限制，很难实现良好的瞬态响应。控制器的死区时间和最小欠阻尼似乎有一定关系。本文推导了在要实现对阶跃参考信号的跟踪控制时，对于具有一个不稳定零点的系统的最小欠阻尼的解析解。通过数值模拟说明了该方法的有效性。

关键词：参考跟踪、最优控制、连续死区控制、性能限制

制御系统并非通过改变控制器类型就可以无限提高控制性能的。制御系统能够实现的响应性能取决于受控对象的动态特性。如果受控对象不具有不稳定零点，只要考虑输入的大小，反向系统就是稳定的，并且可以实现各种过渡响应。然而，具有不稳定零点的受控对象很难按预期进行控制。本论文将考虑具有不稳定零点的受控对象的控制，作为对难以控制对象的兴趣。特别是，控制性能的极限在哪里是一个非常重要且有趣的问题。本论文报道了在具有不稳定零点的受控对象中获得的简单但有趣的分析结果。

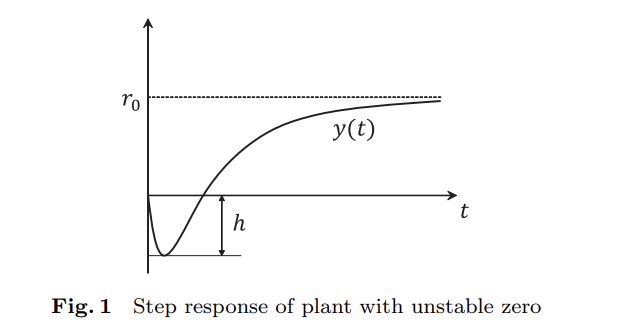
例如，在具有一个实际不稳定零点的受控对象中，已知在进行阶跃目标值追踪时，过渡响应过程中总会出现一定程度的欠阻尼（见图1）。在图1中，信号首先朝相反方向偏移了r0，然后收敛到目标值r0。这种朝相反方向的行为称为欠阻尼，并将其最大值称为欠阻尼量。具有不稳定零点的对象总会出现不同程度的欠阻尼。这是由于控制对象的动态特性导致的控制响应的一种限制。

📚2 运行结果

部分代码：

%%%     condition=1 %zero 1 deadtime 1
%%%     condition=2 %zero 1 Q is 3deg deadtime 5
%%%     condition=3 %zero 2 Q is 4deg deadtime 5
%%% r=other and relative 22(deg=2,refrence=4)
%%%     condition=1 %zero 1
%%%     condition=2 %zero 2
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

deg = 2; %relative degree 1 or 2
reference = 1;%reference 1 ~ 4
condition = 2;

z1 = 1;
z2 = 2;

Lf = 1; %deadbeat time

k_max  = 30;  % kmax 
m      = 30;  % m 

a = 0;   %
b = 0;
c = 0;
d = 0;
f = 0;
g = 0; 
h = 0;
l = 0;

L1 = 0;  %
L2 = 0;
L3 = 0;
L4 = 0;

b10=0;   %
b11 = 0;
b12 = 0;
b13 = 0;
b14 = 0;
b20=0;
b21 = 0;
b22 = 0;
b23 = 0;
b24 = 0;
b30=0;
b31 = 0;
b33 = 0;
b34 = 0;
b44=0;
b43 = 0;
b42 = 0;
b41 = 0;
b40 = 0;
b54=0;
b53 = 0;
b52 = 0;
b51 = 0;
b50 = 0;
b64=0;
b63 = 0;
b62 = 0;
b61 = 0;
b60 = 0;

last_time = 5; %
sample_time=0.01;
t = 0:sample_time:last_time;%
%% pso
xn = 42;                    %
x      = zeros(m,xn);       %
v      = zeros(m,xn);       %
xp     = zeros(m,xn);       %
fxp    = zeros(m,1);        %
fx     = zeros(m,1);        
xg     = zeros(1,xn);       %
fg_log = zeros(k_max+1,1);  %
f_mem  = zeros(k_max,m);    %
keisuu1_log = zeros(m,10,k_max);
keisuu_log = zeros(k_max,10);
number = zeros(k_max,1);
% a~l
alpha = [0 10]; %%

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

🌈4 Matlab代码、数据、文章