【粒子滤波在电池参数估计中的应用】探讨粒子滤波在电池管理系统中的应用，如电池状态估计、参数辨识等，为新能源领域的研究提供参考（Matlab代码实现）

         💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

 ⛳️赠与读者

💥1 概述

粒子滤波在电池参数估计中的应用研究综述

一、粒子滤波（PF）的基本原理与特点

二、电池管理系统的核心需求与挑战

三、粒子滤波在电池状态估计中的应用案例

四、粒子滤波在电池参数辨识中的应用

五、粒子滤波与卡尔曼滤波的性能对比

六、研究现状与挑战

七、结论与展望

📚2 运行结果

🎉3 参考文献 

🌈4 Matlab代码、数据、文档下载

---

 ⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

粒子滤波在电池参数估计中的应用研究综述

一、粒子滤波（PF）的基本原理与特点

粒子滤波是一种基于贝叶斯递归和蒙特卡洛采样的非线性滤波方法，其核心流程包括以下步骤：

1. 

特点：

• 适用于高度非线性、非高斯系统，如电池动态模型。
• 通过离散粒子近似概率分布，无需解析解，灵活性高。
• 计算复杂度随粒子数量增加而显著上升，需权衡精度与效率 。

---

二、电池管理系统的核心需求与挑战

电池管理系统（BMS）需实时监测并估算以下关键参数：

1. 状态估计：
   • 荷电状态（SOC） ：反映剩余电量，要求误差 ≤2% 。
   • 健康状态（SOH） ：表征电池老化程度，需通过容量衰减或内阻变化评估 。
2. 参数辨识：
   • 内阻：与温度、老化程度强相关，需高精度测量（误差 ≤0.3%） 。
   • 容量：直接影响续航能力，需动态跟踪衰减趋势 。
3. 实时性要求：电流采样周期 ≤50ms，电压采样周期 ≤200ms 。

---

三、粒子滤波在电池状态估计中的应用案例

1. SOC估计：
   • LiFePO4电池：基于Thevenin等效电路模型，PF算法相比扩展卡尔曼滤波（EKF）精度提升5%，最大误差低于0.72% 。
   • 温度补偿模型：结合粒子群优化（PSO）改进PF算法，通过自适应权重调整抑制温度干扰，SOC误差稳定在1%以内 。
2. SOH估计：
   • 半机制功率衰减模型：将老化率参数作为状态变量，PF通过实验数据更新后验估计，预测功率衰减趋势 。
   • 双指数退化模型：引入动态布谷鸟搜索算法优化PF重采样，SOH估计误差低于3% 。

典型案例：

• DAEPF算法：结合分数阶等效电路模型，通过多时间尺度联合估计SOC与SOH，最大误差分别控制在2%和5%以内 。
• NASA数据集验证：使用改进PF算法预测电池容量跳水，提前60个循环发出安全预警 。

---

四、粒子滤波在电池参数辨识中的应用

1. 内阻辨识：
   • 等效电路模型：以镍钴铝酸锂电池为例，PF结合最小二乘法辨识模型参数，内阻估计误差 <1% 。
   • 支持向量回归（SVR） ：联合PF预测欧姆内阻突变阈值，提升容量跳水的早期检测能力 。
2. 容量衰减建模：
   • 两时间尺度方法：分层重采样策略下，PF每20小时更新容量估计值，误差较传统方法降低30% 。
   • 随机扰动无迹PF：通过UKF优化粒子分布，容量预测均方误差（RMSE） <2% 。

---

五、粒子滤波与卡尔曼滤波的性能对比

特性	卡尔曼滤波（EKF/UKF）	粒子滤波（PF）
适用系统	线性/轻度非线性高斯系统	强非线性、非高斯系统
计算复杂度	低（解析解）	高（依赖粒子数量）
模型依赖性	需精确模型与噪声统计特性	对模型误差鲁棒性较强
典型应用场景	恒定工况下的SOC估计	动态工况、参数突变（如SOH跳水）
精度对比	在可靠模型下表现优异	模型不精确时优于卡尔曼滤波

案例对比：

• 磷酸铁锂电池SOC估计：PF在温度变化和电流噪声下误差较EKF减少40% 。
• 锂离子电池RUL预测：PF结合OFCLs在模型不精确时预测误差较UKF降低25% 。

---

六、研究现状与挑战

研究进展：

1. 算法优化：
   • 粒子多样性增强：引入灰狼算法、PSO优化粒子分布，抑制退化问题 。
   • 混合模型：结合电化学机理模型与数据驱动方法，提升参数辨识精度 。
2. 多状态联合估计：
   • SOC-SOH协同估计：通过双时间尺度滤波实现参数解耦，降低计算负担 。
   • 端云协同架构：利用云端大数据优化本地PF参数，提升实时性 。

挑战：

1. 计算效率：千级粒子数需求与嵌入式BMS的算力矛盾。
2. 传感器噪声：高噪声环境下粒子权重易失配，需融合鲁棒观测模型 。
3. 长期预测可靠性：容量衰减路径的非平稳性导致RUL预测误差累积 。

---

七、结论与展望

粒子滤波在电池参数估计中展现出独特优势，尤其在非线性、动态工况下的SOC/SOH估计中表现突出。未来研究方向包括：

1. 轻量化算法设计：如基于KLD采样的自适应粒子数控制 。
2. 多物理场耦合建模：整合热-电化学-老化模型，提升参数辨识全面性。
3. 边缘计算应用：通过FPGA/ASIC硬件加速实现实时PF 。

通过持续优化算法与工程化落地，粒子滤波有望成为下一代BMS的核心技术，推动新能源汽车与储能系统的智能化发展。

📚2 运行结果

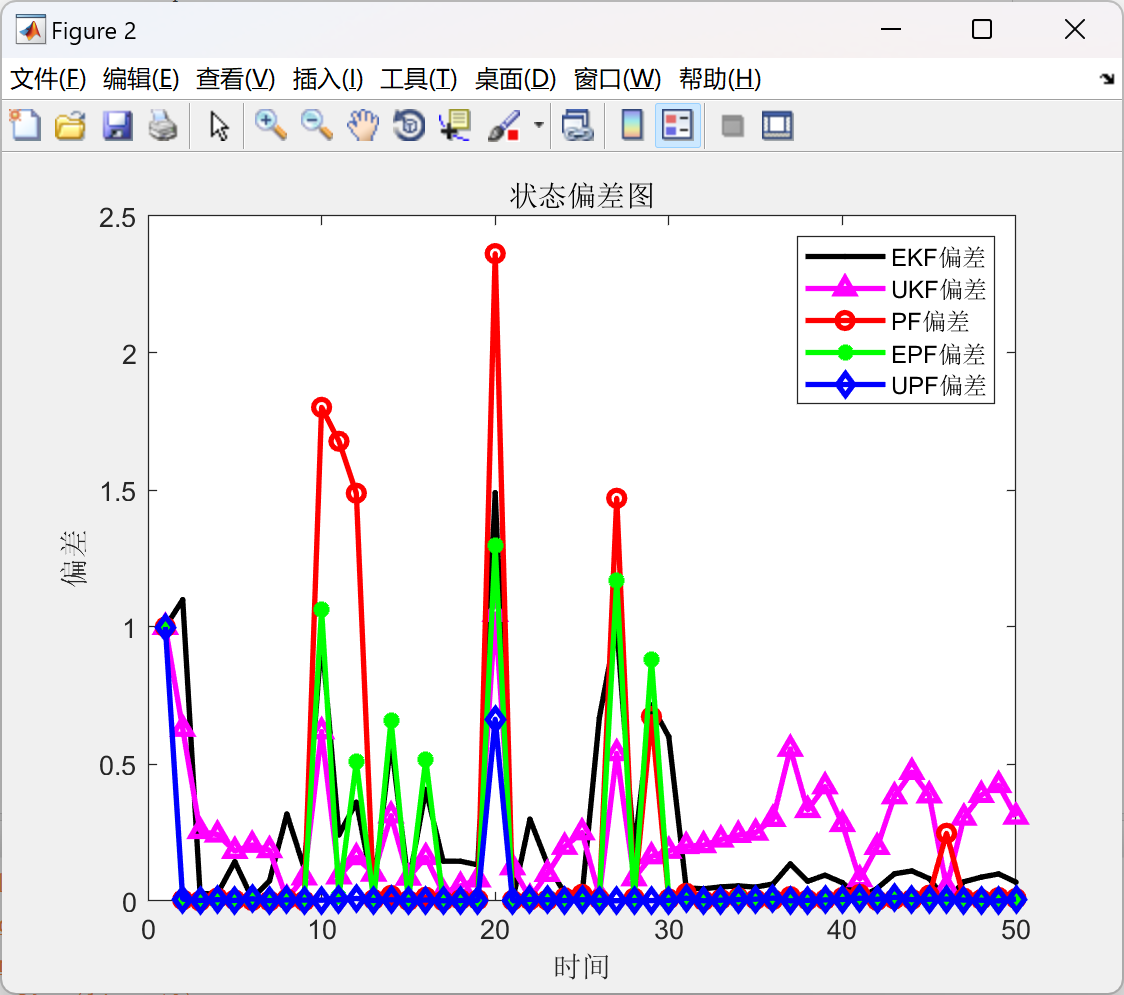
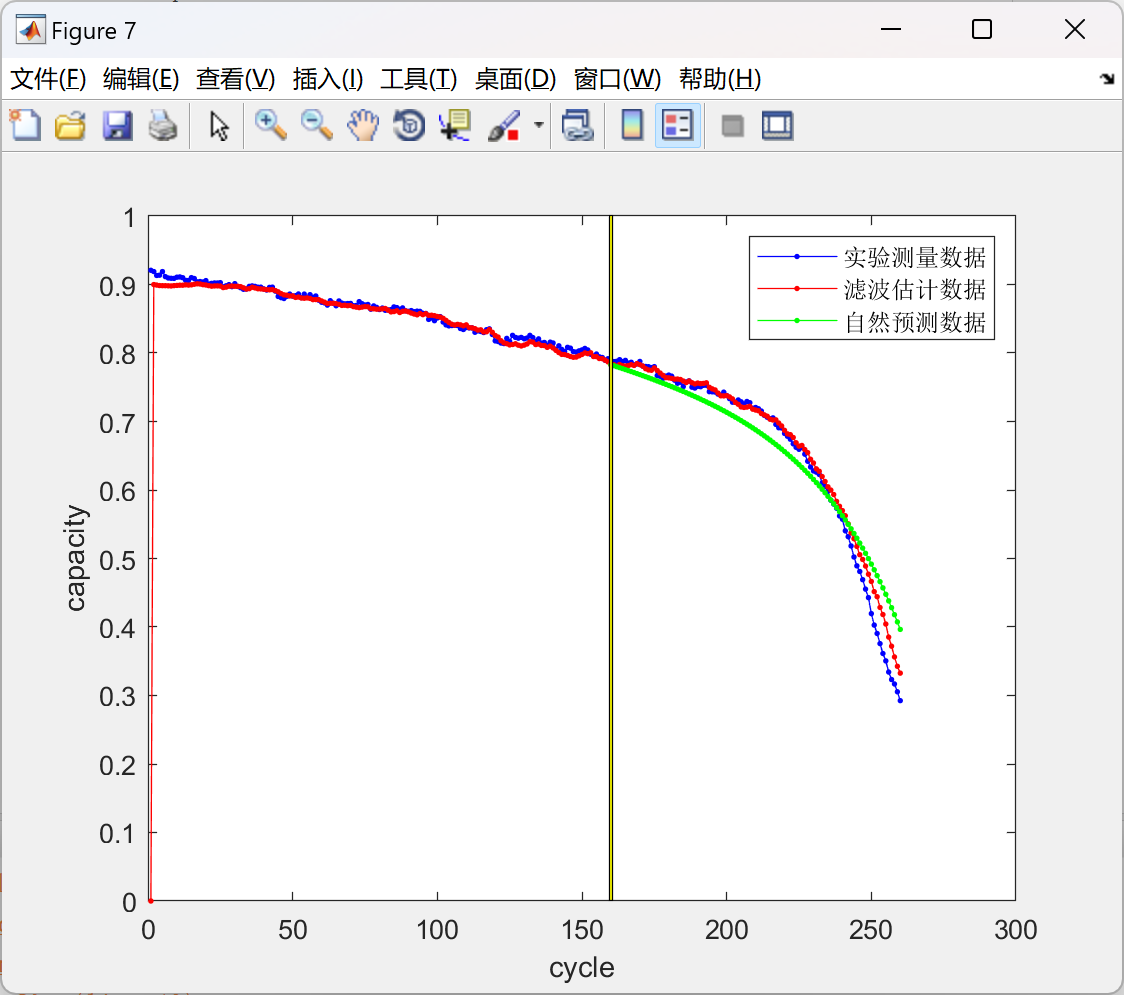
部分代码：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%  函数功能：粒子滤波用于电源寿命预测
function main
% 初始化
% 运行程序时需要将 Battery Capacity.mat 文件复制到程序所在文件夹
load Battery_Capacity
rng(10);
N=length(A12Cycle); %cycle 的总数
M=200; %粒子总数
Future_Cycle=100; %未来趋势
if N>260
    N=260; %清除大于260的数字
end
cita=1e-4;
wa=0.000001;wb=0.01;wc=0.1;wd=0.0001;
Q=cita*diag([wa,wb,wc,wd]); %过程噪声协方差Q
% 驱动矩阵
F=eye(4);
% 观测噪声协方差
R=0.001;
% a,b,c,d赋初值
a=-0.0000083499;b=0.055237;c=0.90097;d=-0.00088543;
X0=[a,b,c,d]';
% 滤波器状态初始化
Xpf=zeros(4,N);
Xpf(:,1)=X0;
% 粒子集初始化
Xm=zeros(4,M,N);
for i=1:M
    Xm(:,i,1)=X0+sqrtm(Q)*randn(4,1);
end
% 观测量
Z(1,1:N)=A12Capacity(1:N,:)';
% 滤波器预测观测zm与x对应
Zm=zeros(1,M,N);
% 滤波器滤波后的观测zp£与Xp£对应
Zpf=zeros(1,N);
% 权值初始化
W=zeros(N,M);
% 粒子滤波算法
for k=2:N
    % 采样
    for i=1:M
        Xm(:,i,k)=F*Xm(:,i,k-1)+sqrtm(Q)*randn(4,1);
    end
    % 重要性权值计算
    for i=1:M
        % 观测预测
        Zm(1,i,k)=hfun(Xm(:,i,k),k);
        % 重要性权值
        W(k,i)=exp(-(Z(1,k)-Zm(1,i,k))^2/2/R)+1e-99;
    end
    % 归一化权值
    W(k,:)=W(k,:)./sum(W(k,:));
    % 重新采样
    outIndex = residualR(1:M,W(k,:)'); %可以选用其他的重采样算法，见第五章
    % 得到新的样本集
    Xm(:,:,k)=Xm(:,outIndex,k);
    % 滤波器滤波后的状态更新为：
    Xpf(:,k)=[mean(Xm(1,:,k));mean(Xm(2,:,k));mean(Xm(3,:,k));mean(Xm(4,:,k))];
    % 用更新后的状态计算Q(k)
    Zpf(1,k)=hfun(Xpf(:,k),k);
end
% 预测未来电容的趋势
% 这里只选择Xpf(:start)点的估计值，按道理是要对前期滤波得到的值做个整体处理的
% 由此导致预测不准确，后续的工作请好好处理Xp(:,1:start)，这个矩阵的数据，平滑
% 处理a，b,c,d然后代入方程预测未来，方能的到更好地效果
start=N-Future_Cycle;
for k=start:N
    Zf(1,k-start+1)=hfun(Xpf(:,start),k);
    Xf(1,k-start+1)=k;
end
Xreal=[a*ones(1,M);b*ones(1,M);c*ones(1,M);d*ones(1,M)];

figure
subplot(2,2,1);
hold on;box on;
plot(Xpf(1,:),'-r.');plot(Xreal(1,:),'-b.')
xlabel('cycle');ylabel('value');
legend('粒子滤波后的a','平均值a')
subplot(2,2,2);
hold on;box on;
plot(Xpf(2,:),'-r.');plot(Xreal(2,:),'-b.')
xlabel('cycle');ylabel('value');
legend('粒子滤波后的b','平均值b')
subplot(2,2,3);
hold on;box on;
plot(Xpf(3,:),'-r.');plot(Xreal(3,:),'-b.')
xlabel('cycle');ylabel('value');
legend('粒子滤波后的c','平均值c')
subplot(2,2,4);
hold on;box on;
plot(Xpf(4,:),'-r.');plot(Xreal(4,:),'-b.')
xlabel('cycle');ylabel('value');
legend('粒子滤波后的d','平均值d')
sgtitle('滤波估计的4个状态参数');
figure
hold on;box on;
h1=plot(Z,'-b.');
h2=plot(Zpf,'-r.');
h3=plot(Xf,Zf,'-g.');
xlabel('cycle');ylabel('capacity');
bar(start,1,'y','DisplayName','none');
legend([h1,h2,h3],'实验测量数据','滤波估计数据','自然预测数据');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

🎉3 参考文献 

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。(文章内容仅供参考，具体效果以运行结果为准)

[1]康明仁.电动汽车锂离子电池荷电状态估计方法研究[D].天津工业大学,2019.

[2]石琴,蒋正信,刘翼闻,等.基于分数阶模型的锂离子电池荷电状态估计[J].机械工程学报, 2024, 60(8):224-232.

[3]焦自权、范兴明、张鑫、罗奕、刘阳升.基于改进粒子滤波算法的锂离子电池状态跟踪与剩余使用寿命预测方法[J].电工技术学报, 2020, 35(18):15.

[4]李佳.锂离子电池组的健康状态估计及寿命预测研究[D].重庆交通大学,2019.

🌈4 Matlab代码、数据、文档下载

资料获取，更多粉丝福利，MATLAB|Simulink|Python资源获取