飞行器学习——坐标系变换（一）：欧拉角法

最新推荐文章于 2025-03-12 15:07:53 发布

ロケット花火君

最新推荐文章于 2025-03-12 15:07:53 发布

阅读量1w

点赞数 5

分类专栏：飞行控制学习

本文链接：https://blog.csdn.net/Zia_CSDN/article/details/105334512

版权

飞行控制学习专栏收录该内容

1 篇文章

订阅专栏

本文深入探讨飞行器领域的坐标轴定义及变换，包括惯性系、地面固定坐标系、航迹坐标系与机体轴系。讲解二维平面坐标系转换原理，通过欧拉角法介绍三维坐标系变换矩阵，提供Z-Y-X旋转顺序下的具体实例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

初识飞行器，第一个绕不开又让人觉得无比头疼的就是坐标轴的定义以及它们之间的变换。

在飞行器领域，主要用到的坐标轴有

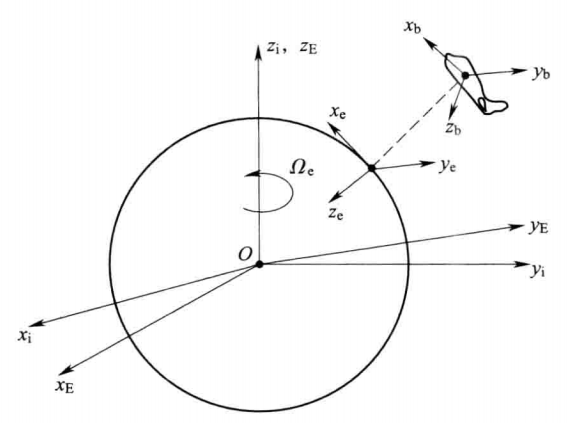
惯性系 $Ox_iy_iz_i$ （宇宙中绝对静止的坐标轴）
地面固定坐标系 $Ox_Ey_Ez_E$ （固定在地球中心，考虑地球自转时适用）
航迹坐标系 $Ox_ey_ez_e$ （坐标原点位于地面， $Ox_e,Oy_e,Oz_e$ 分别指向北向、东向、地心）
机体轴系 Ox_by_bz_b （固连在机体上， $Ox_b,Oy_b,Oz_b$ 分别指向机头、机右、机底）

两个坐标系之间的转换，在飞行动力学中主要有欧拉角法和四元数法等等。

本次主要学习欧拉角法，

首先，针对二维平面坐标系的转换进行分析，如下图，原坐标系 $Oxy$ 逆时针旋转 $\theta$ 角，两个单位向量 $\vec{e_x},\vec{e_y}$ 经过旋转后成为 $\vec{e_x^{'}},\vec{e_y^{'}}$ ，计算两个坐标系之间的转换矩阵 T ，即让等式 $\begin{bmatrix} \vec{e_x^{'}} \\ \vec{e_y^{'}} \\ \end{bmatrix} = T \begin{bmatrix} \vec{e_x} \\ \vec{e_y} \\ \end{bmatrix}$ 成立的 $T$

分别分析两个向量：

$\vec{e_x^{'}}=|\vec{e_x^{'}}|cos\theta\vec{e_x}+|\vec{e_x^{'}}|sin\theta\vec{e_y} \\ =cos\theta\vec{e_x}+sin\theta\vec{e_y} \vec{e_y^{'}}=-|\vec{e_y^{'}}|sin\theta\vec{e_x}+|\vec{e_y^{'}}|cos\theta\vec{e_y} \\ =-sin\theta\vec{e_x}+cos\theta\vec{e_y}$

整理成紧凑形式：

$\begin{bmatrix} \vec{e_x^{'}} \\ \vec{e_y^{'}} \\ \end{bmatrix} = \begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \\ \end{bmatrix} \begin{bmatrix} \vec{e_x} \\ \vec{e_y} \\ \end{bmatrix}$

如果我们这时候再加上一条垂直屏幕向外的 $Oz$ 轴，上面的步骤我们可以描述成绕 $Oz$ 轴逆时针旋转 $\theta$ 角，那么上述的式子就可以扩维成

$\begin{bmatrix} \vec{e_x^{'}} \\ \vec{e_y^{'}} \\ \vec{e_z^{'}} \\ \end{bmatrix} = \begin{bmatrix} cos\theta & sin\theta & 0 \\ -sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \vec{e_x} \\ \vec{e_y} \\ \vec{e_z} \\ \end{bmatrix}$

读者们可以自行按照这个步骤推导一下顺时针旋转情况下的变换矩阵。

在三维环境下，也就有三个轴的旋转，根据坐标轴转换顺序的不同，这三个矩阵按不同顺序相乘可以分别获得不同的最终坐标系变换矩阵

看到这密密麻麻的字母，我当时是有撕课本的冲动的。

想到撕了还要给图书馆还一本新的，贫穷又使我恢复了理智。

下面给出三个轴旋转的基元旋转矩阵，以上所有的公式都是从这些基元旋转矩阵推出的：（Tips：实际计算时需注意顺时针或逆时针旋转）

绕X轴的旋转变换矩阵为： $R_x(\theta_x) = \begin{bmatrix} 1 & 0 & 0\\ 0 & cos\theta_x & -sin\theta_x\\0 & sin\theta_x & cos\theta_x \end{bmatrix}$

绕Y轴的旋转变换矩阵为： $R_y(\theta_y) = \begin{bmatrix} cos\theta_y & 0 & sin\theta_y\\0 & 1 & 0\\-sin\theta_y & 0 & cos\theta_y \end{bmatrix}$

绕Z轴的旋转变换矩阵为： $R_z(\theta_z) = \begin{bmatrix} cos\theta_z & -sin\theta_z & 0\\sin\theta_z & cos\theta_z & 0\\0 & 0 & 1 \end{bmatrix}$

按照飞行器建模时常用的Z-Y-X旋转顺序，经过验算，与上图中的答案相同。

%% 计算ZYX旋转顺序下的坐标系变换矩阵 syms cx sx cy sy cz sz 
Rx = [1 0 0; 0 cx -sx; 0 sx cx]; 
Ry = [cy 0 sy; 0 1 0; -sy 0 cy]; 
Rz = [cz -sz 0; sz cz 0; 0 0 1]; 
Rz * Ry * Rx 


--------运行以上程序-------- 

ans = 
[ cy*cz, cz*sx*sy - cx*sz, sx*sz + cx*cz*sy] 
[ cy*sz, cx*cz + sx*sy*sz, cx*sy*sz - cz*sx] 
[ -sy, cy*sx, cx*cy]