版权声明:本文为博主原创文章,转载请附上博文链接!
四、一睹EKF2芳容(上接牢记公式,ardupilot EKF2就是纸老虎(四))
更新
本博客讲解EKF算法“更新过程“的几个公式。还是先重复下EKF2使用的几个核心公式。
在EKF2实际的应用中,过程噪声矩阵
中有些元素是非加性的,有些不是。观测噪声矩阵
中的元素都是加性的,所以上面的公式可以化简为如下公式:
预测
预测状态估计:
预测协方差估计:
更新
创新或计算剩余
创新(或残差)协方差
接近最优的卡尔曼增益
更新状态估计
更新的协方差估计
状态转移矩阵和观测矩阵被定义为以下雅克比行列式:
矩阵
被定义为以下雅克比行列式:
状态转移模型和观测模型如下:
过程噪声矩阵
中有些元素是非加性的,有些是加性的,所以在EKF2的实现中,预测协方差估计方程中的协方差矩阵
有些元素加的是
有些加的是
。
EKF2在实现EKF”更新过程“方程时,通过它的代码可以看出来它是分块进行的。
// Run the EKF equations to estimate at the fusion time horizon if new IMU data is available in the buffer
if (runUpdates) {
// Predict states using IMU data from the delayed time horizon
UpdateStrapdownEquationsNED();
// Predict the covariance growth
CovariancePrediction();
// Update states using magnetometer data
SelectMagFusion();
// Update states using GPS and altimeter data
SelectVelPosFusion();
// Update states using range beacon data
SelectRngBcnFusion();
// Update states using optical flow data
SelectFlowFusion();
// Update states using airspeed data
SelectTasFusion();
// Update states using sideslip constraint assumption for fly-forward vehicles
SelectBetaFusion();
// Update the filter status
updateFilterStatus();
}下面的这几个函数,执行的都是“更新过程”
// Update states using magnetometer data
// 使用电子磁罗盘的数据修正偏航角,通过公式,它有可能也修正俯仰和横滚,但目前还不明确
SelectMagFusion();
// Update states using GPS and altimeter data
// 通过GPS、气压计、测距仪修正速度和位置
SelectVelPosFusion();
//下面4个函数我也没有深入的看,尚不清楚其用途
// Update states using range beacon data
SelectRngBcnFusion();
// Update states using optical flow data
SelectFlowFusion();
// Update states using airspeed data
SelectTasFusion();
// Update states using sideslip constraint assumption for fly-forward vehicles
SelectBetaFusion();下面我以函数SelectMagFusion()为例,说明下“更新过程”即这几个公式在代码中是怎么实现的。
更新
创新或计算剩余
创新(或残差)协方差
接近最优的卡尔曼增益
更新状态估计
更新的协方差估计
状态转移矩阵和观测矩阵被定义为以下雅克比行列式:
状态转移模型和观测模型如下:
通过看上述的几个式子,你应该已经知道了, 在这一部分中,确定 ,求观测矩阵
,求观测矩阵 是关键。以使用磁罗盘数据为例。
是关键。以使用磁罗盘数据为例。
它的观测模型如下
magMeas = transpose(Tbn)*[magN;magE;magD] + [magX;magY;magZ]; % predicted measurement
这个应该不难理解,测量到的三轴磁通量应该是地磁场在北东地坐标系下的值旋转到机体坐标系下再加上机体坐标系下磁通量的补偿(这个补偿来自于磁罗盘和机体坐标系的差异,如果完全对齐,这个值应该是0)。
% 观测模型
magMeas = transpose(Tbn)*[magN;magE;magD] + [magX;magY;magZ]; % predicted measurement
% 求解观测矩阵,并化简
H_MAG = jacobian(magMeas,stateVector); % measurement Jacobian
% 设置'rotErrX', 'rotErrY', 'rotErrZ'为0
H_MAG = subs(H_MAG, {'rotErrX', 'rotErrY', 'rotErrZ'}, {0,0,0});
[H_MAG,SH_MAG]=OptimiseAlgebra(H_MAG,'SH_MAG');
% 求解卡尔曼增益
K_MX = (P*transpose(H_MAG(1,:)))/(H_MAG(1,:)*P*transpose(H_MAG(1,:)) + R_MAG); % Kalman gain vector
[K_MX,SK_MX]=OptimiseAlgebra(K_MX,'SK_MX');
K_MY = (P*transpose(H_MAG(2,:)))/(H_MAG(2,:)*P*transpose(H_MAG(2,:)) + R_MAG); % Kalman gain vector
[K_MY,SK_MY]=OptimiseAlgebra(K_MY,'SK_MY');
K_MZ = (P*transpose(H_MAG(3,:)))/(H_MAG(3,:)*P*transpose(H_MAG(3,:)) + R_MAG); % Kalman gain vector
[K_MZ,SK_MZ]=OptimiseAlgebra(K_MZ,'SK_MZ');
% save equations and reset workspace
save('Magnetometer.mat','SH_MAG','H_MAG','SK_MX','K_MX','SK_MY','K_MY','SK_MZ','K_MZ');
通过上述脚本语言就求出了观测矩阵 和卡尔曼增益
和卡尔曼增益 ,
, 也有了,
也有了, 是磁罗盘测量出来的值,
是磁罗盘测量出来的值, 也就求出来了。多了在这儿多说一句,
也就求出来了。多了在这儿多说一句, 上面带一个 ^(小尖),表示
上面带一个 ^(小尖),表示 的估计,为什么是估计呢,因为它是又估计值
的估计,为什么是估计呢,因为它是又估计值 和
和 算出来的,所以它也是个估计值。
算出来的,所以它也是个估计值。
到这儿其实就结束了,但如果你这么想,证明你忽略了一个细节那就是观测矩阵 求解的方程
求解的方程 ,对函数
,对函数 在
在 处求一阶偏导。而根据前面所说的
处求一阶偏导。而根据前面所说的 应该是上一时刻的最优估计
应该是上一时刻的最优估计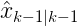
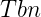
% define the quaternion rotation vector for the state estimate
estQuat = [q0;q1;q2;q3];
% define the attitude error rotation vector, where error = truth - estimate
errRotVec = [rotErrX;rotErrY;rotErrZ];
% define the attitude error quaternion using a first order linearisation
errQuat = [1;0.5*errRotVec];
% Define the truth quaternion as the estimate + error
truthQuat = QuatMult(estQuat, errQuat);
% derive the truth body to nav direction cosine matrix
Tbn = Quat2Tbn(truthQuat);
它也是上一时刻的(rotErrX,rotErrY,rotErrZ在计算 时被设置为0)。而根据公式
时被设置为0)。而根据公式
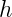
 。
。
实际上,上一时刻的估计值和当前时刻的估计值,所表示的物理量是一致的,当前时刻的估计值只是在上一时刻的最优估计值基础上做了一些数学运算而已。所以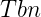
 都是上一时刻最优估计值或当前时刻估计值,本质上是一样的。化简后的数学计算是一样的。
都是上一时刻最优估计值或当前时刻估计值,本质上是一样的。化简后的数学计算是一样的。
EKF2中的实现如下
/*
* Fuse magnetometer measurements using explicit algebraic equations generated with Matlab symbolic toolbox.
* The script file used to generate these and other equations in this filter can be found here:
* https://github.com/priseborough/InertialNav/blob/master/derivations/RotationVectorAttitudeParameterisation/GenerateNavFilterEquations.m
*/
void NavEKF2_core::FuseMagnetometer()
{
hal.util->perf_begin(_perf_test[1]);
// declarations
ftype &q0 = mag_state.q0;
ftype &q1 = mag_state.q1;
ftype &q2 = mag_state.q2;
ftype &q3 = mag_state.q3;
ftype &magN = mag_state.magN;
ftype &magE = mag_state.magE;
ftype &magD = mag_state.magD;
ftype &magXbias = mag_state.magXbias;
ftype &magYbias = mag_state.magYbias;
ftype &magZbias = mag_state.magZbias;
uint8_t &obsIndex = mag_state.obsIndex;
Matrix3f &DCM = mag_state.DCM;
Vector3f &MagPred = mag_state.MagPred;
ftype &R_MAG = mag_state.R_MAG;
ftype *SH_MAG = &mag_state.SH_MAG[0];
Vector24 H_MAG;
Vector6 SK_MX;
Vector6 SK_MY;
Vector6 SK_MZ;
hal.util->perf_end(_perf_test[1]);
// perform sequential fusion of magnetometer measurements.
// this assumes that the errors in the different components are
// uncorrelated which is not true, however in the absence of covariance
// data fit is the only assumption we can make
// so we might as well take advantage of the computational efficiencies
// associated with sequential fusion
// calculate observation jacobians and Kalman gains
if (obsIndex == 0)
{
hal.util->perf_begin(_perf_test[2]);
// copy required states to local variable names
q0 = stateStruct.quat[0];
q1 = stateStruct.quat[1];
q2 = stateStruct.quat[2];
q3 = stateStruct.quat[3];
magN = stateStruct.earth_magfield[0];
magE = stateStruct.earth_magfield[1];
magD = stateStruct.earth_magfield[2];
magXbias = stateStruct.body_magfield[0];
magYbias = stateStruct.body_magfield[1];
magZbias = stateStruct.body_magfield[2];
// rotate predicted earth components into body axes and calculate
// predicted measurements
DCM[0][0] = q0*q0 + q1*q1 - q2*q2 - q3*q3;
DCM[0][1] = 2.0f*(q1*q2 + q0*q3);
DCM[0][2] = 2.0f*(q1*q3-q0*q2);
DCM[1][0] = 2.0f*(q1*q2 - q0*q3);
DCM[1][1] = q0*q0 - q1*q1 + q2*q2 - q3*q3;
DCM[1][2] = 2.0f*(q2*q3 + q0*q1);
DCM[2][0] = 2.0f*(q1*q3 + q0*q2);
DCM[2][1] = 2.0f*(q2*q3 - q0*q1);
DCM[2][2] = q0*q0 - q1*q1 - q2*q2 + q3*q3;
MagPred[0] = DCM[0][0]*magN + DCM[0][1]*magE + DCM[0][2]*magD + magXbias;
MagPred[1] = DCM[1][0]*magN + DCM[1][1]*magE + DCM[1][2]*magD + magYbias;
MagPred[2] = DCM[2][0]*magN + DCM[2][1]*magE + DCM[2][2]*magD + magZbias;
// calculate the measurement innovation for each axis
for (uint8_t i = 0; i<=2; i++) {
innovMag[i] = MagPred[i] - magDataDelayed.mag[i];
}
// scale magnetometer observation error with total angular rate to allow for timing errors
R_MAG = sq(constrain_float(frontend->_magNoise, 0.01f, 0.5f)) + sq(frontend->magVarRateScale*delAngCorrected.length() / imuDataDelayed.delAngDT);
// calculate common expressions used to calculate observation jacobians an innovation variance for each component
SH_MAG[0] = sq(q0) - sq(q1) + sq(q2) - sq(q3);
SH_MAG[1] = sq(q0) + sq(q1) - sq(q2) - sq(q3);
SH_MAG[2] = sq(q0) - sq(q1) - sq(q2) + sq(q3);
SH_MAG[3] = 2.0f*q0*q1 + 2.0f*q2*q3;
SH_MAG[4] = 2.0f*q0*q3 + 2.0f*q1*q2;
SH_MAG[5] = 2.0f*q0*q2 + 2.0f*q1*q3;
SH_MAG[6] = magE*(2.0f*q0*q1 - 2.0f*q2*q3);
SH_MAG[7] = 2.0f*q1*q3 - 2.0f*q0*q2;
SH_MAG[8] = 2.0f*q0*q3;
// Calculate the innovation variance for each axis
// X axis
varInnovMag[0] = (P[19][19] + R_MAG - P[1][19]*(magD*SH_MAG[2] - SH_MAG[6] + magN*SH_MAG[5]) + P[16][19]*SH_MAG[1] + P[17][19]*SH_MAG[4] + P[18][19]*SH_MAG[7] + P[2][19]*(magE*SH_MAG[0] + magD*SH_MAG[3] - magN*(SH_MAG[8] - 2.0f*q1*q2)) - (magD*SH_MAG[2] - SH_MAG[6] + magN*SH_MAG[5])*(P[19][1] - P[1][1]*(magD*SH_MAG[2] - SH_MAG[6] + magN*SH_MAG[5]) + P[16][1]*SH_MAG[1] + P[17][1]*SH_MAG[4] + P[18][1]*SH_MAG[7] + P[2][1]*(magE*SH_MAG[0] + magD*SH_MAG[3] - magN*(SH_MAG[8] - 2.0f*q1*q2))) + SH_MAG[1]*(P[19][16] - P[1][16]*(magD*SH_MAG[2] - SH_MAG[6] + magN*SH_MAG[5]) + P[16][16]*SH_MAG[1] + P[17][16]*SH_MAG[4] + P[18][16]*SH_MAG[7] + P[2][16]*(magE*SH_MAG[0] + magD*SH_MAG[3] - magN*(SH_MAG[8] - 2.0f*q1*q2))) + SH_MAG[4]*(P[19][17] - P[1][17]*(magD*SH_MAG[2] - SH_MAG[6] + magN*SH_MAG[5]) + P[16][17]*SH_MAG[1] + P[17][17]*SH_MAG[4] + P[18][17]*SH_MAG[7] + P[2][17]*(magE*SH_MAG[0] + magD*SH_MAG[3] - magN*(SH_MAG[8] - 2.0f*q1*q2))) + SH_MAG[7]*(P[19][18] - P[1][18]*(magD*SH_MAG[2] - SH_MAG[6] + magN*SH_MAG[5]) + P[16][18]*SH_MAG[1] + P[17][18]*SH_MAG[4] + P[18][18]*SH_MAG[7] + P[2][18]*(magE*SH_MAG[0] + magD*SH_MAG[3] - magN*(SH_MAG[8] - 2.0f*q1*q2))) + (magE*SH_MAG[0] + magD*SH_MAG[3] - magN*(SH_MAG[8] - 2.0f*q1*q2))*(P[19][2] - P[1][2]*(magD*SH_MAG[2] - SH_MAG[6] + magN*SH_MAG[5]) + P[16][2]*SH_MAG[1] + P[17][2]*SH_MAG[4] + P[18][2]*SH_MAG[7] + P[2][2]*(magE*SH_MAG[0] + magD*SH_MAG[3] - magN*(SH_MAG[8] - 2.0f*q1*q2))));
if (varInnovMag[0] >= R_MAG) {
faultStatus.bad_xmag = false;
} else {
// the calculation is badly conditioned, so we cannot perform fusion on this step
// we reset the covariance matrix and try again next measurement
CovarianceInit();
obsIndex = 1;
faultStatus.bad_xmag = true;
hal.util->perf_end(_perf_test[2]);
return;
}
// Y axis
varInnovMag[1] = (P[20][20] + R_MAG + P[0][20]*(magD*SH_MAG[2] - SH_MAG[6] + magN*SH_MAG[5]) + P[17][20]*SH_MAG[0] + P[18][20]*SH_MAG[3] - (SH_MAG[8] - 2.0f*q1*q2)*(P[20][16] + P[0][16]*(magD*SH_MAG[2] - SH_MAG[6] + magN*SH_MAG[5]) + P[17][16]*SH_MAG[0] + P[18][16]*SH_MAG[3] - P[2][16]*(magE*SH_MAG[4] + magD*SH_MAG[7] + magN*SH_MAG[1]) - P[16][16]*(SH_MAG[8] - 2.0f*q1*q2)) - P[2][20]*(magE*SH_MAG[4] + magD*SH_MAG[7] + magN*SH_MAG[1]) + (magD*SH_MAG[2] - SH_MAG[6] + magN*SH_MAG[5])*(P[20][0] + P[0][0]*(magD*SH_MAG[2] - SH_MAG[6] + magN*SH_MAG[5]) + P[17][0]*SH_MAG[0] + P[18][0]*SH_MAG[3] - P[2][0]*(magE*SH_MAG[4] + magD*SH_MAG[7] + magN*SH_MAG[1]) - P[16][0]*(SH_MAG[8] - 2.0f*q1*q2)) + SH_MAG[0]*(P[20][17] + P[0][17]*(magD*SH_MAG[2] - SH_MAG[6] + magN*SH_MAG[5]) + P[17][17]*SH_MAG[0] + P[18][17]*SH_MAG[3] - P[2][17]*(magE*SH_MAG[4] + magD*SH_MAG[7] + magN*SH_MAG[1]) - P[16][17]*(SH_MAG[8] - 2.0f*q1*q2)) + SH_MAG[3]*(P[20][18] + P[0][18]*(magD*SH_MAG[2] - SH_MAG[6] + magN*SH_MAG[5]) + P[17][18]*SH_MAG[0] + P[18][18]*SH_MAG[3] - P[2][18]*(magE*SH_MAG[4] + magD*SH_MAG[7] + magN*SH_MAG[1]) - P[16][18]*(SH_MAG[8] - 2.0f*q1*q2)) - P[16][20]*(SH_MAG[8] - 2.0f*q1*q2) - (magE*SH_MAG[4] + magD*SH_MAG[7] + magN*SH_MAG[1])*(P[20][2] + P[0][2]*(magD*SH_MAG[2] - SH_MAG[6] + magN*SH_MAG[5]) + P[17][2]*SH_MAG[0] + P[18][2]*SH_MAG[3] - P[2][2]*(magE*SH_MAG[4] + magD*SH_MAG[7] + magN*SH_MAG[1]) - P[16][2]*(SH_MAG[8] - 2.0f*q1*q2)));
if (varInnovMag[1] >= R_MAG) {
faultStatus.bad_ymag = false;
} else {
// the calculation is badly conditioned, so we cannot perform fusion on this step
// we reset the covariance matrix and try again next measurement
CovarianceInit();
obsIndex = 2;
faultStatus.bad_ymag = true;
hal.util->perf_end(_perf_test[2]);
return;
}
// Z axis
varInnovMag[2] = (P[21][21] + R_MAG + P[16][21]*SH_MAG[5] + P[18][21]*SH_MAG[2] - (2.0f*q0*q1 - 2.0f*q2*q3)*(P[21][17] + P[16][17]*SH_MAG[5] + P[18][17]*SH_MAG[2] - P[0][17]*(magE*SH_MAG[0] + magD*SH_MAG[3] - magN*(SH_MAG[8] - 2.0f*q1*q2)) + P[1][17]*(magE*SH_MAG[4] + magD*SH_MAG[7] + magN*SH_MAG[1]) - P[17][17]*(2.0f*q0*q1 - 2.0f*q2*q3)) - P[0][21]*(magE*SH_MAG[0] + magD*SH_MAG[3] - magN*(SH_MAG[8] - 2.0f*q1*q2)) + P[1][21]*(magE*SH_MAG[4] + magD*SH_MAG[7] + magN*SH_MAG[1]) + SH_MAG[5]*(P[21][16] + P[16][16]*SH_MAG[5] + P[18][16]*SH_MAG[2] - P[0][16]*(magE*SH_MAG[0] + magD*SH_MAG[3] - magN*(SH_MAG[8] - 2.0f*q1*q2)) + P[1][16]*(magE*SH_MAG[4] + magD*SH_MAG[7] + magN*SH_MAG[1]) - P[17][16]*(2.0f*q0*q1 - 2.0f*q2*q3)) + SH_MAG[2]*(P[21][18] + P[16][18]*SH_MAG[5] + P[18][18]*SH_MAG[2] - P[0][18]*(magE*SH_MAG[0] + magD*SH_MAG[3] - magN*(SH_MAG[8] - 2.0f*q1*q2)) + P[1][18]*(magE*SH_MAG[4] + magD*SH_MAG[7] + magN*SH_MAG[1]) - P[17][18]*(2.0f*q0*q1 - 2.0f*q2*q3)) - (magE*SH_MAG[0] + magD*SH_MAG[3] - magN*(SH_MAG[8] - 2.0f*q1*q2))*(P[21][0] + P[16][0]*SH_MAG[5] + P[18][0]*SH_MAG[2] - P[0][0]*(magE*SH_MAG[0] + magD*SH_MAG[3] - magN*(SH_MAG[8] - 2.0f*q1*q2)) + P[1][0]*(magE*SH_MAG[4] + magD*SH_MAG[7] + magN*SH_MAG[1]) - P[17][0]*(2.0f*q0*q1 - 2.0f*q2*q3)) - P[17][21]*(2.0f*q0*q1 - 2.0f*q2*q3) + (magE*SH_MAG[4] + magD*SH_MAG[7] + magN*SH_MAG[1])*(P[21][1] + P[16][1]*SH_MAG[5] + P[18][1]*SH_MAG[2] - P[0][1]*(magE*SH_MAG[0] + magD*SH_MAG[3] - magN*(SH_MAG[8] - 2.0f*q1*q2)) + P[1][1]*(magE*SH_MAG[4] + magD*SH_MAG[7] + magN*SH_MAG[1]) - P[17][1]*(2.0f*q0*q1 - 2.0f*q2*q3)));
if (varInnovMag[2] >= R_MAG) {
faultStatus.bad_zmag = false;
} else {
// the calculation is badly conditioned, so we cannot perform fusion on this step
// we reset the covariance matrix and try again next measurement
CovarianceInit();
obsIndex = 3;
faultStatus.bad_zmag = true;
hal.util->perf_end(_perf_test[2]);
return;
}
// calculate the innovation test ratios
for (uint8_t i = 0; i<=2; i++) {
magTestRatio[i] = sq(innovMag[i]) / (sq(MAX(0.01f * (float)frontend->_magInnovGate, 1.0f)) * varInnovMag[i]);
}
// check the last values from all components and set magnetometer health accordingly
magHealth = (magTestRatio[0] < 1.0f && magTestRatio[1] < 1.0f && magTestRatio[2] < 1.0f);
// if the magnetometer is unhealthy, do not proceed further
if (!magHealth) {
hal.util->perf_end(_perf_test[2]);
return;
}
for (uint8_t i = 0; i<=stateIndexLim; i++) H_MAG[i] = 0.0f;
H_MAG[1] = SH_MAG[6] - magD*SH_MAG[2] - magN*SH_MAG[5];
H_MAG[2] = magE*SH_MAG[0] + magD*SH_MAG[3] - magN*(SH_MAG[8] - 2.0f*q1*q2);
H_MAG[16] = SH_MAG[1];
H_MAG[17] = SH_MAG[4];
H_MAG[18] = SH_MAG[7];
H_MAG[19] = 1.0f;
// calculate Kalman gain
SK_MX[0] = 1.0f / varInnovMag[0];
SK_MX[1] = magE*SH_MAG[0] + magD*SH_MAG[3] - magN*(SH_MAG[8] - 2.0f*q1*q2);
SK_MX[2] = magD*SH_MAG[2] - SH_MAG[6] + magN*SH_MAG[5];
SK_MX[3] = SH_MAG[7];
Kfusion[0] = SK_MX[0]*(P[0][19] + P[0][16]*SH_MAG[1] + P[0][17]*SH_MAG[4] - P[0][1]*SK_MX[2] + P[0][2]*SK_MX[1] + P[0][18]*SK_MX[3]);
Kfusion[1] = SK_MX[0]*(P[1][19] + P[1][16]*SH_MAG[1] + P[1][17]*SH_MAG[4] - P[1][1]*SK_MX[2] + P[1][2]*SK_MX[1] + P[1][18]*SK_MX[3]);
Kfusion[2] = SK_MX[0]*(P[2][19] + P[2][16]*SH_MAG[1] + P[2][17]*SH_MAG[4] - P[2][1]*SK_MX[2] + P[2][2]*SK_MX[1] + P[2][18]*SK_MX[3]);
Kfusion[3] = SK_MX[0]*(P[3][19] + P[3][16]*SH_MAG[1] + P[3][17]*SH_MAG[4] - P[3][1]*SK_MX[2] + P[3][2]*SK_MX[1] + P[3][18]*SK_MX[3]);
Kfusion[4] = SK_MX[0]*(P[4][19] + P[4][16]*SH_MAG[1] + P[4][17]*SH_MAG[4] - P[4][1]*SK_MX[2] + P[4][2]*SK_MX[1] + P[4][18]*SK_MX[3]);
Kfusion[5] = SK_MX[0]*(P[5][19] + P[5][16]*SH_MAG[1] + P[5][17]*SH_MAG[4] - P[5][1]*SK_MX[2] + P[5][2]*SK_MX[1] + P[5][18]*SK_MX[3]);
Kfusion[6] = SK_MX[0]*(P[6][19] + P[6][16]*SH_MAG[1] + P[6][17]*SH_MAG[4] - P[6][1]*SK_MX[2] + P[6][2]*SK_MX[1] + P[6][18]*SK_MX[3]);
Kfusion[7] = SK_MX[0]*(P[7][19] + P[7][16]*SH_MAG[1] + P[7][17]*SH_MAG[4] - P[7][1]*SK_MX[2] + P[7][2]*SK_MX[1] + P[7][18]*SK_MX[3]);
Kfusion[8] = SK_MX[0]*(P[8][19] + P[8][16]*SH_MAG[1] + P[8][17]*SH_MAG[4] - P[8][1]*SK_MX[2] + P[8][2]*SK_MX[1] + P[8][18]*SK_MX[3]);
Kfusion[9] = SK_MX[0]*(P[9][19] + P[9][16]*SH_MAG[1] + P[9][17]*SH_MAG[4] - P[9][1]*SK_MX[2] + P[9][2]*SK_MX[1] + P[9][18]*SK_MX[3]);
Kfusion[10] = SK_MX[0]*(P[10][19] + P[10][16]*SH_MAG[1] + P[10][17]*SH_MAG[4] - P[10][1]*SK_MX[2] + P[10][2]*SK_MX[1] + P[10][18]*SK_MX[3]);
Kfusion[11] = SK_MX[0]*(P[11][19] + P[11][16]*SH_MAG[1] + P[11][17]*SH_MAG[4] - P[11][1]*SK_MX[2] + P[11][2]*SK_MX[1] + P[11][18]*SK_MX[3]);
Kfusion[12] = SK_MX[0]*(P[12][19] + P[12][16]*SH_MAG[1] + P[12][17]*SH_MAG[4] - P[12][1]*SK_MX[2] + P[12][2]*SK_MX[1] + P[12][18]*SK_MX[3]);
Kfusion[13] = SK_MX[0]*(P[13][19] + P[13][16]*SH_MAG[1] + P[13][17]*SH_MAG[4] - P[13][1]*SK_MX[2] + P[13][2]*SK_MX[1] + P[13][18]*SK_MX[3]);
Kfusion[14] = SK_MX[0]*(P[14][19] + P[14][16]*SH_MAG[1] + P[14][17]*SH_MAG[4] - P[14][1]*SK_MX[2] + P[14][2]*SK_MX[1] + P[14][18]*SK_MX[3]);
Kfusion[15] = SK_MX[0]*(P[15][19] + P[15][16]*SH_MAG[1] + P[15][17]*SH_MAG[4] - P[15][1]*SK_MX[2] + P[15][2]*SK_MX[1] + P[15][18]*SK_MX[3]);
// end perf block
// zero Kalman gains to inhibit wind state estimation
if (!inhibitWindStates) {
Kfusion[22] = SK_MX[0]*(P[22][19] + P[22][16]*SH_MAG[1] + P[22][17]*SH_MAG[4] - P[22][1]*SK_MX[2] + P[22][2]*SK_MX[1] + P[22][18]*SK_MX[3]);
Kfusion[23] = SK_MX[0]*(P[23][19] + P[23][16]*SH_MAG[1] + P[23][17]*SH_MAG[4] - P[23][1]*SK_MX[2] + P[23][2]*SK_MX[1] + P[23][18]*SK_MX[3]);
} else {
Kfusion[22] = 0.0f;
Kfusion[23] = 0.0f;
}
// zero Kalman gains to inhibit magnetic field state estimation
if (!inhibitMagStates) {
Kfusion[16] = SK_MX[0]*(P[16][19] + P[16][16]*SH_MAG[1] + P[16][17]*SH_MAG[4] - P[16][1]*SK_MX[2] + P[16][2]*SK_MX[1] + P[16][18]*SK_MX[3]);
Kfusion[17] = SK_MX[0]*(P[17][19] + P[17][16]*SH_MAG[1] + P[17][17]*SH_MAG[4] - P[17][1]*SK_MX[2] + P[17][2]*SK_MX[1] + P[17][18]*SK_MX[3]);
Kfusion[18] = SK_MX[0]*(P[18][19] + P[18][16]*SH_MAG[1] + P[18][17]*SH_MAG[4] - P[18][1]*SK_MX[2] + P[18][2]*SK_MX[1] + P[18][18]*SK_MX[3]);
Kfusion[19] = SK_MX[0]*(P[19][19] + P[19][16]*SH_MAG[1] + P[19][17]*SH_MAG[4] - P[19][1]*SK_MX[2] + P[19][2]*SK_MX[1] + P[19][18]*SK_MX[3]);
Kfusion[20] = SK_MX[0]*(P[20][19] + P[20][16]*SH_MAG[1] + P[20][17]*SH_MAG[4] - P[20][1]*SK_MX[2] + P[20][2]*SK_MX[1] + P[20][18]*SK_MX[3]);
Kfusion[21] = SK_MX[0]*(P[21][19] + P[21][16]*SH_MAG[1] + P[21][17]*SH_MAG[4] - P[21][1]*SK_MX[2] + P[21][2]*SK_MX[1] + P[21][18]*SK_MX[3]);
} else {
for (uint8_t i=16; i<=21; i++) {
Kfusion[i] = 0.0f;
}
}
// reset the observation index to 0 (we start by fusing the X measurement)
obsIndex = 0;
// set flags to indicate to other processes that fusion has been performed and is required on the next frame
// this can be used by other fusion processes to avoid fusing on the same frame as this expensive step
magFusePerformed = true;
magFuseRequired = true;
hal.util->perf_end(_perf_test[2]);
}
else if (obsIndex == 1) // we are now fusing the Y measurement
{
hal.util->perf_begin(_perf_test[3]);
// calculate observation jacobians
for (uint8_t i = 0; i<=stateIndexLim; i++) H_MAG[i] = 0.0f;
H_MAG[0] = magD*SH_MAG[2] - SH_MAG[6] + magN*SH_MAG[5];
H_MAG[2] = - magE*SH_MAG[4] - magD*SH_MAG[7] - magN*SH_MAG[1];
H_MAG[16] = 2.0f*q1*q2 - SH_MAG[8];
H_MAG[17] = SH_MAG[0];
H_MAG[18] = SH_MAG[3];
H_MAG[20] = 1.0f;
// calculate Kalman gain
SK_MY[0] = 1.0f / varInnovMag[1];
SK_MY[1] = magE*SH_MAG[4] + magD*SH_MAG[7] + magN*SH_MAG[1];
SK_MY[2] = magD*SH_MAG[2] - SH_MAG[6] + magN*SH_MAG[5];
SK_MY[3] = SH_MAG[8] - 2.0f*q1*q2;
Kfusion[0] = SK_MY[0]*(P[0][20] + P[0][17]*SH_MAG[0] + P[0][18]*SH_MAG[3] + P[0][0]*SK_MY[2] - P[0][2]*SK_MY[1] - P[0][16]*SK_MY[3]);
Kfusion[1] = SK_MY[0]*(P[1][20] + P[1][17]*SH_MAG[0] + P[1][18]*SH_MAG[3] + P[1][0]*SK_MY[2] - P[1][2]*SK_MY[1] - P[1][16]*SK_MY[3]);
Kfusion[2] = SK_MY[0]*(P[2][20] + P[2][17]*SH_MAG[0] + P[2][18]*SH_MAG[3] + P[2][0]*SK_MY[2] - P[2][2]*SK_MY[1] - P[2][16]*SK_MY[3]);
Kfusion[3] = SK_MY[0]*(P[3][20] + P[3][17]*SH_MAG[0] + P[3][18]*SH_MAG[3] + P[3][0]*SK_MY[2] - P[3][2]*SK_MY[1] - P[3][16]*SK_MY[3]);
Kfusion[4] = SK_MY[0]*(P[4][20] + P[4][17]*SH_MAG[0] + P[4][18]*SH_MAG[3] + P[4][0]*SK_MY[2] - P[4][2]*SK_MY[1] - P[4][16]*SK_MY[3]);
Kfusion[5] = SK_MY[0]*(P[5][20] + P[5][17]*SH_MAG[0] + P[5][18]*SH_MAG[3] + P[5][0]*SK_MY[2] - P[5][2]*SK_MY[1] - P[5][16]*SK_MY[3]);
Kfusion[6] = SK_MY[0]*(P[6][20] + P[6][17]*SH_MAG[0] + P[6][18]*SH_MAG[3] + P[6][0]*SK_MY[2] - P[6][2]*SK_MY[1] - P[6][16]*SK_MY[3]);
Kfusion[7] = SK_MY[0]*(P[7][20] + P[7][17]*SH_MAG[0] + P[7][18]*SH_MAG[3] + P[7][0]*SK_MY[2] - P[7][2]*SK_MY[1] - P[7][16]*SK_MY[3]);
Kfusion[8] = SK_MY[0]*(P[8][20] + P[8][17]*SH_MAG[0] + P[8][18]*SH_MAG[3] + P[8][0]*SK_MY[2] - P[8][2]*SK_MY[1] - P[8][16]*SK_MY[3]);
Kfusion[9] = SK_MY[0]*(P[9][20] + P[9][17]*SH_MAG[0] + P[9][18]*SH_MAG[3] + P[9][0]*SK_MY[2] - P[9][2]*SK_MY[1] - P[9][16]*SK_MY[3]);
Kfusion[10] = SK_MY[0]*(P[10][20] + P[10][17]*SH_MAG[0] + P[10][18]*SH_MAG[3] + P[10][0]*SK_MY[2] - P[10][2]*SK_MY[1] - P[10][16]*SK_MY[3]);
Kfusion[11] = SK_MY[0]*(P[11][20] + P[11][17]*SH_MAG[0] + P[11][18]*SH_MAG[3] + P[11][0]*SK_MY[2] - P[11][2]*SK_MY[1] - P[11][16]*SK_MY[3]);
Kfusion[12] = SK_MY[0]*(P[12][20] + P[12][17]*SH_MAG[0] + P[12][18]*SH_MAG[3] + P[12][0]*SK_MY[2] - P[12][2]*SK_MY[1] - P[12][16]*SK_MY[3]);
Kfusion[13] = SK_MY[0]*(P[13][20] + P[13][17]*SH_MAG[0] + P[13][18]*SH_MAG[3] + P[13][0]*SK_MY[2] - P[13][2]*SK_MY[1] - P[13][16]*SK_MY[3]);
Kfusion[14] = SK_MY[0]*(P[14][20] + P[14][17]*SH_MAG[0] + P[14][18]*SH_MAG[3] + P[14][0]*SK_MY[2] - P[14][2]*SK_MY[1] - P[14][16]*SK_MY[3]);
Kfusion[15] = SK_MY[0]*(P[15][20] + P[15][17]*SH_MAG[0] + P[15][18]*SH_MAG[3] + P[15][0]*SK_MY[2] - P[15][2]*SK_MY[1] - P[15][16]*SK_MY[3]);
// zero Kalman gains to inhibit wind state estimation
if (!inhibitWindStates) {
Kfusion[22] = SK_MY[0]*(P[22][20] + P[22][17]*SH_MAG[0] + P[22][18]*SH_MAG[3] + P[22][0]*SK_MY[2] - P[22][2]*SK_MY[1] - P[22][16]*SK_MY[3]);
Kfusion[23] = SK_MY[0]*(P[23][20] + P[23][17]*SH_MAG[0] + P[23][18]*SH_MAG[3] + P[23][0]*SK_MY[2] - P[23][2]*SK_MY[1] - P[23][16]*SK_MY[3]);
} else {
Kfusion[22] = 0.0f;
Kfusion[23] = 0.0f;
}
// zero Kalman gains to inhibit magnetic field state estimation
if (!inhibitMagStates) {
Kfusion[16] = SK_MY[0]*(P[16][20] + P[16][17]*SH_MAG[0] + P[16][18]*SH_MAG[3] + P[16][0]*SK_MY[2] - P[16][2]*SK_MY[1] - P[16][16]*SK_MY[3]);
Kfusion[17] = SK_MY[0]*(P[17][20] + P[17][17]*SH_MAG[0] + P[17][18]*SH_MAG[3] + P[17][0]*SK_MY[2] - P[17][2]*SK_MY[1] - P[17][16]*SK_MY[3]);
Kfusion[18] = SK_MY[0]*(P[18][20] + P[18][17]*SH_MAG[0] + P[18][18]*SH_MAG[3] + P[18][0]*SK_MY[2] - P[18][2]*SK_MY[1] - P[18][16]*SK_MY[3]);
Kfusion[19] = SK_MY[0]*(P[19][20] + P[19][17]*SH_MAG[0] + P[19][18]*SH_MAG[3] + P[19][0]*SK_MY[2] - P[19][2]*SK_MY[1] - P[19][16]*SK_MY[3]);
Kfusion[20] = SK_MY[0]*(P[20][20] + P[20][17]*SH_MAG[0] + P[20][18]*SH_MAG[3] + P[20][0]*SK_MY[2] - P[20][2]*SK_MY[1] - P[20][16]*SK_MY[3]);
Kfusion[21] = SK_MY[0]*(P[21][20] + P[21][17]*SH_MAG[0] + P[21][18]*SH_MAG[3] + P[21][0]*SK_MY[2] - P[21][2]*SK_MY[1] - P[21][16]*SK_MY[3]);
} else {
for (uint8_t i=16; i<=21; i++) {
Kfusion[i] = 0.0f;
}
}
// set flags to indicate to other processes that fusion has been performede and is required on the next frame
// this can be used by other fusion processes to avoid fusing on the same frame as this expensive step
magFusePerformed = true;
magFuseRequired = true;
hal.util->perf_end(_perf_test[3]);
}
else if (obsIndex == 2) // we are now fusing the Z measurement
{
hal.util->perf_begin(_perf_test[4]);
// calculate observation jacobians
for (uint8_t i = 0; i<=stateIndexLim; i++) H_MAG[i] = 0.0f;
H_MAG[0] = magN*(SH_MAG[8] - 2.0f*q1*q2) - magD*SH_MAG[3] - magE*SH_MAG[0];
H_MAG[1] = magE*SH_MAG[4] + magD*SH_MAG[7] + magN*SH_MAG[1];
H_MAG[16] = SH_MAG[5];
H_MAG[17] = 2.0f*q2*q3 - 2.0f*q0*q1;
H_MAG[18] = SH_MAG[2];
H_MAG[21] = 1.0f;
// calculate Kalman gain
SK_MZ[0] = 1.0f / varInnovMag[2];
SK_MZ[1] = magE*SH_MAG[0] + magD*SH_MAG[3] - magN*(SH_MAG[8] - 2.0f*q1*q2);
SK_MZ[2] = magE*SH_MAG[4] + magD*SH_MAG[7] + magN*SH_MAG[1];
SK_MZ[3] = 2.0f*q0*q1 - 2.0f*q2*q3;
Kfusion[0] = SK_MZ[0]*(P[0][21] + P[0][18]*SH_MAG[2] + P[0][16]*SH_MAG[5] - P[0][0]*SK_MZ[1] + P[0][1]*SK_MZ[2] - P[0][17]*SK_MZ[3]);
Kfusion[1] = SK_MZ[0]*(P[1][21] + P[1][18]*SH_MAG[2] + P[1][16]*SH_MAG[5] - P[1][0]*SK_MZ[1] + P[1][1]*SK_MZ[2] - P[1][17]*SK_MZ[3]);
Kfusion[2] = SK_MZ[0]*(P[2][21] + P[2][18]*SH_MAG[2] + P[2][16]*SH_MAG[5] - P[2][0]*SK_MZ[1] + P[2][1]*SK_MZ[2] - P[2][17]*SK_MZ[3]);
Kfusion[3] = SK_MZ[0]*(P[3][21] + P[3][18]*SH_MAG[2] + P[3][16]*SH_MAG[5] - P[3][0]*SK_MZ[1] + P[3][1]*SK_MZ[2] - P[3][17]*SK_MZ[3]);
Kfusion[4] = SK_MZ[0]*(P[4][21] + P[4][18]*SH_MAG[2] + P[4][16]*SH_MAG[5] - P[4][0]*SK_MZ[1] + P[4][1]*SK_MZ[2] - P[4][17]*SK_MZ[3]);
Kfusion[5] = SK_MZ[0]*(P[5][21] + P[5][18]*SH_MAG[2] + P[5][16]*SH_MAG[5] - P[5][0]*SK_MZ[1] + P[5][1]*SK_MZ[2] - P[5][17]*SK_MZ[3]);
Kfusion[6] = SK_MZ[0]*(P[6][21] + P[6][18]*SH_MAG[2] + P[6][16]*SH_MAG[5] - P[6][0]*SK_MZ[1] + P[6][1]*SK_MZ[2] - P[6][17]*SK_MZ[3]);
Kfusion[7] = SK_MZ[0]*(P[7][21] + P[7][18]*SH_MAG[2] + P[7][16]*SH_MAG[5] - P[7][0]*SK_MZ[1] + P[7][1]*SK_MZ[2] - P[7][17]*SK_MZ[3]);
Kfusion[8] = SK_MZ[0]*(P[8][21] + P[8][18]*SH_MAG[2] + P[8][16]*SH_MAG[5] - P[8][0]*SK_MZ[1] + P[8][1]*SK_MZ[2] - P[8][17]*SK_MZ[3]);
Kfusion[9] = SK_MZ[0]*(P[9][21] + P[9][18]*SH_MAG[2] + P[9][16]*SH_MAG[5] - P[9][0]*SK_MZ[1] + P[9][1]*SK_MZ[2] - P[9][17]*SK_MZ[3]);
Kfusion[10] = SK_MZ[0]*(P[10][21] + P[10][18]*SH_MAG[2] + P[10][16]*SH_MAG[5] - P[10][0]*SK_MZ[1] + P[10][1]*SK_MZ[2] - P[10][17]*SK_MZ[3]);
Kfusion[11] = SK_MZ[0]*(P[11][21] + P[11][18]*SH_MAG[2] + P[11][16]*SH_MAG[5] - P[11][0]*SK_MZ[1] + P[11][1]*SK_MZ[2] - P[11][17]*SK_MZ[3]);
Kfusion[12] = SK_MZ[0]*(P[12][21] + P[12][18]*SH_MAG[2] + P[12][16]*SH_MAG[5] - P[12][0]*SK_MZ[1] + P[12][1]*SK_MZ[2] - P[12][17]*SK_MZ[3]);
Kfusion[13] = SK_MZ[0]*(P[13][21] + P[13][18]*SH_MAG[2] + P[13][16]*SH_MAG[5] - P[13][0]*SK_MZ[1] + P[13][1]*SK_MZ[2] - P[13][17]*SK_MZ[3]);
Kfusion[14] = SK_MZ[0]*(P[14][21] + P[14][18]*SH_MAG[2] + P[14][16]*SH_MAG[5] - P[14][0]*SK_MZ[1] + P[14][1]*SK_MZ[2] - P[14][17]*SK_MZ[3]);
Kfusion[15] = SK_MZ[0]*(P[15][21] + P[15][18]*SH_MAG[2] + P[15][16]*SH_MAG[5] - P[15][0]*SK_MZ[1] + P[15][1]*SK_MZ[2] - P[15][17]*SK_MZ[3]);
// zero Kalman gains to inhibit wind state estimation
if (!inhibitWindStates) {
Kfusion[22] = SK_MZ[0]*(P[22][21] + P[22][18]*SH_MAG[2] + P[22][16]*SH_MAG[5] - P[22][0]*SK_MZ[1] + P[22][1]*SK_MZ[2] - P[22][17]*SK_MZ[3]);
Kfusion[23] = SK_MZ[0]*(P[23][21] + P[23][18]*SH_MAG[2] + P[23][16]*SH_MAG[5] - P[23][0]*SK_MZ[1] + P[23][1]*SK_MZ[2] - P[23][17]*SK_MZ[3]);
} else {
Kfusion[22] = 0.0f;
Kfusion[23] = 0.0f;
}
// zero Kalman gains to inhibit magnetic field state estimation
if (!inhibitMagStates) {
Kfusion[16] = SK_MZ[0]*(P[16][21] + P[16][18]*SH_MAG[2] + P[16][16]*SH_MAG[5] - P[16][0]*SK_MZ[1] + P[16][1]*SK_MZ[2] - P[16][17]*SK_MZ[3]);
Kfusion[17] = SK_MZ[0]*(P[17][21] + P[17][18]*SH_MAG[2] + P[17][16]*SH_MAG[5] - P[17][0]*SK_MZ[1] + P[17][1]*SK_MZ[2] - P[17][17]*SK_MZ[3]);
Kfusion[18] = SK_MZ[0]*(P[18][21] + P[18][18]*SH_MAG[2] + P[18][16]*SH_MAG[5] - P[18][0]*SK_MZ[1] + P[18][1]*SK_MZ[2] - P[18][17]*SK_MZ[3]);
Kfusion[19] = SK_MZ[0]*(P[19][21] + P[19][18]*SH_MAG[2] + P[19][16]*SH_MAG[5] - P[19][0]*SK_MZ[1] + P[19][1]*SK_MZ[2] - P[19][17]*SK_MZ[3]);
Kfusion[20] = SK_MZ[0]*(P[20][21] + P[20][18]*SH_MAG[2] + P[20][16]*SH_MAG[5] - P[20][0]*SK_MZ[1] + P[20][1]*SK_MZ[2] - P[20][17]*SK_MZ[3]);
Kfusion[21] = SK_MZ[0]*(P[21][21] + P[21][18]*SH_MAG[2] + P[21][16]*SH_MAG[5] - P[21][0]*SK_MZ[1] + P[21][1]*SK_MZ[2] - P[21][17]*SK_MZ[3]);
} else {
for (uint8_t i=16; i<=21; i++) {
Kfusion[i] = 0.0f;
}
}
// set flags to indicate to other processes that fusion has been performede and is required on the next frame
// this can be used by other fusion processes to avoid fusing on the same frame as this expensive step
magFusePerformed = true;
magFuseRequired = false;
hal.util->perf_end(_perf_test[4]);
}
hal.util->perf_begin(_perf_test[5]);
// correct the covariance P = (I - K*H)*P
// take advantage of the empty columns in KH to reduce the
// number of operations
for (unsigned i = 0; i<=stateIndexLim; i++) {
for (unsigned j = 0; j<=2; j++) {
KH[i][j] = Kfusion[i] * H_MAG[j];
}
for (unsigned j = 3; j<=15; j++) {
KH[i][j] = 0.0f;
}
for (unsigned j = 16; j<=21; j++) {
KH[i][j] = Kfusion[i] * H_MAG[j];
}
for (unsigned j = 22; j<=23; j++) {
KH[i][j] = 0.0f;
}
}
for (unsigned j = 0; j<=stateIndexLim; j++) {
for (unsigned i = 0; i<=stateIndexLim; i++) {
ftype res = 0;
res += KH[i][0] * P[0][j];
res += KH[i][1] * P[1][j];
res += KH[i][2] * P[2][j];
res += KH[i][16] * P[16][j];
res += KH[i][17] * P[17][j];
res += KH[i][18] * P[18][j];
res += KH[i][19] * P[19][j];
res += KH[i][20] * P[20][j];
res += KH[i][21] * P[21][j];
KHP[i][j] = res;
}
}
// Check that we are not going to drive any variances negative and skip the update if so
bool healthyFusion = true;
for (uint8_t i= 0; i<=stateIndexLim; i++) {
if (KHP[i][i] > P[i][i]) {
healthyFusion = false;
}
}
if (healthyFusion) {
// update the covariance matrix
for (uint8_t i= 0; i<=stateIndexLim; i++) {
for (uint8_t j= 0; j<=stateIndexLim; j++) {
P[i][j] = P[i][j] - KHP[i][j];
}
}
// force the covariance matrix to be symmetrical and limit the variances to prevent ill-condiioning.
ForceSymmetry();
ConstrainVariances();
// update the states
// zero the attitude error state - by definition it is assumed to be zero before each observaton fusion
stateStruct.angErr.zero();
// correct the state vector
for (uint8_t j= 0; j<=stateIndexLim; j++) {
statesArray[j] = statesArray[j] - Kfusion[j] * innovMag[obsIndex];
}
// the first 3 states represent the angular misalignment vector. This is
// is used to correct the estimated quaternion on the current time step
stateStruct.quat.rotate(stateStruct.angErr);
} else {
// record bad axis
if (obsIndex == 0) {
faultStatus.bad_xmag = true;
} else if (obsIndex == 1) {
faultStatus.bad_ymag = true;
} else if (obsIndex == 2) {
faultStatus.bad_zmag = true;
}
CovarianceInit();
hal.util->perf_end(_perf_test[5]);
return;
}
hal.util->perf_end(_perf_test[5]);
}在EKF2中,还有一个函数是对偏航角做简单的修正,在函数NavEKF2_core::fuseEulerYaw()中,所用的公式如下
%% derive equations for fusion of 321 sequence yaw measurement
load('StatePrediction.mat');
% Calculate the yaw (first rotation) angle from the 321 rotation sequence
angMeas = atan(Tbn(2,1)/Tbn(1,1));
H_YAW321 = jacobian(angMeas,stateVector); % measurement Jacobian
H_YAW321 = subs(H_YAW321, {'rotErrX', 'rotErrY', 'rotErrZ'}, {0,0,0});
H_YAW321 = simplify(H_YAW321);
ccode(H_YAW321,'file','calcH_YAW321.c');
fix_c_code('calcH_YAW321.c');
% reset workspace
clear all;
reset(symengine);
%% derive equations for fusion of 312 sequence yaw measurement
load('StatePrediction.mat');
% Calculate the yaw (first rotation) angle from an Euler 312 sequence
angMeas = atan(-Tbn(1,2)/Tbn(2,2));
H_YAW312 = jacobian(angMeas,stateVector); % measurement Jacobianclea
H_YAW312 = subs(H_YAW312, {'rotErrX', 'rotErrY', 'rotErrZ'}, {0,0,0});
H_YAW312 = simplify(H_YAW312);
ccode(H_YAW312,'file','calcH_YAW312.c');
fix_c_code('calcH_YAW312.c');
% reset workspace
clear all;
reset(symengine);
EKF2中的代码如下
/*
* Fuse magnetic heading measurement using explicit algebraic equations generated with Matlab symbolic toolbox.
* The script file used to generate these and other equations in this filter can be found here:
* https://github.com/priseborough/InertialNav/blob/master/derivations/RotationVectorAttitudeParameterisation/GenerateNavFilterEquations.m
* This fusion method only modifies the orientation, does not require use of the magnetic field states and is computationally cheaper.
* It is suitable for use when the external magnetic field environment is disturbed (eg close to metal structures, on ground).
* It is not as robust to magnetometer failures.
* It is not suitable for operation where the horizontal magnetic field strength is weak (within 30 degrees latitude of the the magnetic poles)
*/
void NavEKF2_core::fuseEulerYaw()
{
float q0 = stateStruct.quat[0];
float q1 = stateStruct.quat[1];
float q2 = stateStruct.quat[2];
float q3 = stateStruct.quat[3];
// compass measurement error variance (rad^2)
const float R_YAW = sq(frontend->_yawNoise);
// calculate observation jacobian, predicted yaw and zero yaw body to earth rotation matrix
// determine if a 321 or 312 Euler sequence is best
float predicted_yaw;
float measured_yaw;
float H_YAW[3];
Matrix3f Tbn_zeroYaw;
if (fabsf(prevTnb[0][2]) < fabsf(prevTnb[1][2])) {
// calculate observation jacobian when we are observing the first rotation in a 321 sequence
float t2 = q0*q0;
float t3 = q1*q1;
float t4 = q2*q2;
float t5 = q3*q3;
float t6 = t2+t3-t4-t5;
float t7 = q0*q3*2.0f;
float t8 = q1*q2*2.0f;
float t9 = t7+t8;
float t10 = sq(t6);
if (t10 > 1e-6f) {
t10 = 1.0f / t10;
} else {
return;
}
float t11 = t9*t9;
float t12 = t10*t11;
float t13 = t12+1.0f;
float t14;
if (fabsf(t13) > 1e-3f) {
t14 = 1.0f/t13;
} else {
return;
}
float t15 = 1.0f/t6;
H_YAW[0] = 0.0f;
H_YAW[1] = t14*(t15*(q0*q1*2.0f-q2*q3*2.0f)+t9*t10*(q0*q2*2.0f+q1*q3*2.0f));
H_YAW[2] = t14*(t15*(t2-t3+t4-t5)+t9*t10*(t7-t8));
// calculate predicted and measured yaw angle
Vector3f euler321;
stateStruct.quat.to_euler(euler321.x, euler321.y, euler321.z);
predicted_yaw = euler321.z;
if (use_compass() && yawAlignComplete && magStateInitComplete) {
// Use measured mag components rotated into earth frame to measure yaw
Tbn_zeroYaw.from_euler(euler321.x, euler321.y, 0.0f);
Vector3f magMeasNED = Tbn_zeroYaw*magDataDelayed.mag;
measured_yaw = wrap_PI(-atan2f(magMeasNED.y, magMeasNED.x) + _ahrs->get_compass()->get_declination());
} else if (extNavUsedForYaw) {
// Get the yaw angle from the external vision data
extNavDataDelayed.quat.to_euler(euler321.x, euler321.y, euler321.z);
measured_yaw = euler321.z;
} else {
// no data so use predicted to prevent unconstrained variance growth
measured_yaw = predicted_yaw;
}
} else {
// calculate observaton jacobian when we are observing a rotation in a 312 sequence
float t2 = q0*q0;
float t3 = q1*q1;
float t4 = q2*q2;
float t5 = q3*q3;
float t6 = t2-t3+t4-t5;
float t7 = q0*q3*2.0f;
float t10 = q1*q2*2.0f;
float t8 = t7-t10;
float t9 = sq(t6);
if (t9 > 1e-6f) {
t9 = 1.0f/t9;
} else {
return;
}
float t11 = t8*t8;
float t12 = t9*t11;
float t13 = t12+1.0f;
float t14;
if (fabsf(t13) > 1e-3f) {
t14 = 1.0f/t13;
} else {
return;
}
float t15 = 1.0f/t6;
H_YAW[0] = -t14*(t15*(q0*q2*2.0+q1*q3*2.0)-t8*t9*(q0*q1*2.0-q2*q3*2.0));
H_YAW[1] = 0.0f;
H_YAW[2] = t14*(t15*(t2+t3-t4-t5)+t8*t9*(t7+t10));
// calculate predicted and measured yaw angle
Vector3f euler312 = stateStruct.quat.to_vector312();
predicted_yaw = euler312.z;
if (use_compass() && yawAlignComplete && magStateInitComplete) {
// Use measured mag components rotated into earth frame to measure yaw
Tbn_zeroYaw.from_euler312(euler312.x, euler312.y, 0.0f);
Vector3f magMeasNED = Tbn_zeroYaw*magDataDelayed.mag;
measured_yaw = wrap_PI(-atan2f(magMeasNED.y, magMeasNED.x) + _ahrs->get_compass()->get_declination());
} else if (extNavUsedForYaw) {
// Get the yaw angle from the external vision data
euler312 = extNavDataDelayed.quat.to_vector312();
measured_yaw = euler312.z;
} else {
// no data so use predicted to prevent unconstrained variance growth
measured_yaw = predicted_yaw;
}
}
// Calculate the innovation
float innovation = wrap_PI(predicted_yaw - measured_yaw);
// Copy raw value to output variable used for data logging
innovYaw = innovation;
// Calculate innovation variance and Kalman gains, taking advantage of the fact that only the first 3 elements in H are non zero
float PH[3];
float varInnov = R_YAW;
for (uint8_t rowIndex=0; rowIndex<=2; rowIndex++) {
PH[rowIndex] = 0.0f;
for (uint8_t colIndex=0; colIndex<=2; colIndex++) {
PH[rowIndex] += P[rowIndex][colIndex]*H_YAW[colIndex];
}
varInnov += H_YAW[rowIndex]*PH[rowIndex];
}
float varInnovInv;
if (varInnov >= R_YAW) {
varInnovInv = 1.0f / varInnov;
// output numerical health status
faultStatus.bad_yaw = false;
} else {
// the calculation is badly conditioned, so we cannot perform fusion on this step
// we reset the covariance matrix and try again next measurement
CovarianceInit();
// output numerical health status
faultStatus.bad_yaw = true;
return;
}
// calculate Kalman gain
for (uint8_t rowIndex=0; rowIndex<=stateIndexLim; rowIndex++) {
Kfusion[rowIndex] = 0.0f;
for (uint8_t colIndex=0; colIndex<=2; colIndex++) {
Kfusion[rowIndex] += P[rowIndex][colIndex]*H_YAW[colIndex];
}
Kfusion[rowIndex] *= varInnovInv;
}
// calculate the innovation test ratio
yawTestRatio = sq(innovation) / (sq(MAX(0.01f * (float)frontend->_yawInnovGate, 1.0f)) * varInnov);
// Declare the magnetometer unhealthy if the innovation test fails
if (yawTestRatio > 1.0f) {
magHealth = false;
// On the ground a large innovation could be due to large initial gyro bias or magnetic interference from nearby objects
// If we are flying, then it is more likely due to a magnetometer fault and we should not fuse the data
if (inFlight) {
return;
}
} else {
magHealth = true;
}
// limit the innovation so that initial corrections are not too large
if (innovation > 0.5f) {
innovation = 0.5f;
} else if (innovation < -0.5f) {
innovation = -0.5f;
}
// correct the covariance using P = P - K*H*P taking advantage of the fact that only the first 3 elements in H are non zero
// calculate K*H*P
for (uint8_t row = 0; row <= stateIndexLim; row++) {
for (uint8_t column = 0; column <= 2; column++) {
KH[row][column] = Kfusion[row] * H_YAW[column];
}
}
for (uint8_t row = 0; row <= stateIndexLim; row++) {
for (uint8_t column = 0; column <= stateIndexLim; column++) {
float tmp = KH[row][0] * P[0][column];
tmp += KH[row][1] * P[1][column];
tmp += KH[row][2] * P[2][column];
KHP[row][column] = tmp;
}
}
// Check that we are not going to drive any variances negative and skip the update if so
bool healthyFusion = true;
for (uint8_t i= 0; i<=stateIndexLim; i++) {
if (KHP[i][i] > P[i][i]) {
healthyFusion = false;
}
}
if (healthyFusion) {
// update the covariance matrix
for (uint8_t i= 0; i<=stateIndexLim; i++) {
for (uint8_t j= 0; j<=stateIndexLim; j++) {
P[i][j] = P[i][j] - KHP[i][j];
}
}
// force the covariance matrix to be symmetrical and limit the variances to prevent ill-condiioning.
ForceSymmetry();
ConstrainVariances();
// zero the attitude error state - by definition it is assumed to be zero before each observaton fusion
stateStruct.angErr.zero();
// correct the state vector
for (uint8_t i=0; i<=stateIndexLim; i++) {
statesArray[i] -= Kfusion[i] * innovation;
}
// the first 3 states represent the angular misalignment vector. This is
// is used to correct the estimated quaternion on the current time step
stateStruct.quat.rotate(stateStruct.angErr);
// record fusion event
faultStatus.bad_yaw = false;
lastYawTime_ms = imuSampleTime_ms;
} else {
// record fusion numerical health status
faultStatus.bad_yaw = true;
}
}这部分我就不再做详细的解释了,核心的思想还是和刚才的一样,有兴趣的你可以自己推导下(眼过千遍,不如手过一边)。
对于 观测模型 的选择,是和你的测量数据直接相关的,磁罗盘是这样,通过GPS、气压计、测距仪修正速度、位置就不是这样了。因为GPS、气压计、测距仪锁测量的位置信息、速度信息、都是北东地坐标系下的,而状态向量中的这些信息也是北东地坐标系下的,他们是直接观测的,所以观测模型可以忽略,也就是GPS、气压计、测距仪修正速度、位置时,观测矩阵
的选择,是和你的测量数据直接相关的,磁罗盘是这样,通过GPS、气压计、测距仪修正速度、位置就不是这样了。因为GPS、气压计、测距仪锁测量的位置信息、速度信息、都是北东地坐标系下的,而状态向量中的这些信息也是北东地坐标系下的,他们是直接观测的,所以观测模型可以忽略,也就是GPS、气压计、测距仪修正速度、位置时,观测矩阵 是单位矩阵。
是单位矩阵。
写道这里,算是将EKF2对照这EKF理论梳理了一部分,对于使用空速计、光流传感器、等其他传感器修正状态向量的代码,我也没有仔细的看过,所以我也就不再讲解了(以免误人子弟),但修正的过程肯定都是上面我所得这些。GenerateNavFilterEquations.m脚本中的其他内容就是在算我没说的那几个传感器修正状态向量时所使用的观测矩阵、卡尔曼增益等。GenerateNavFilterEquations.m中还有一些内容是将这些公式计算生成C代码的,这个通过函数的名字可以看出来。我所讲的这些,都是基于ardupilot 3.5.2版本的。在这个版本中EKF还有个升级版的实现EKF3,我不大清楚之后的版本,EKF3有没有改动,目前ardupilot的最新版本为3.6.4-rc1,如果想要了解EKF3,我建议在这个版本或更新的版本上了解。EKF3所使用的脚本名字还没有变GenerateNavFilterEquations.m,但来源变了。这里有一些关于EKF3相关的介绍文档。
花了几天的时间,匆匆的完成了这个系列,其中肯定有很多的错别字或描述错误的地方,如果你看到了,希望你能将错误的地方,在留言中指出。
回顾学习EKF2的过程,感慨良多。从连四元数、旋转矢量是什么都不知道,到对扩展卡尔曼滤波器有一定的了解,再到现在,这两年多的时间真切的感受到了学习是个螺旋上升的过程,当你实在看不下去的时候,不妨去了解下EKF相关的其他知识或其他你感兴趣的知识。说不准你学习的哪点知识帮助你在学习EKF的路上又向前的迈了一步。在这期间你一定不要忘记想要了解EKF的这件事,时常的思考、像刷微博那样看看相关的资料,你总会离目的地越来越近。最后送上我喜欢的两句话:










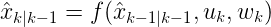
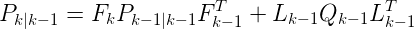




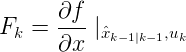

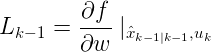















 965
965

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








