▲基于16PSK调制解调+LDPC编译码通信链路matlab误码率仿真

最新推荐文章于 2025-04-30 14:27:27 发布

fpga和matlab

最新推荐文章于 2025-04-30 14:27:27 发布

阅读量725

点赞数 34

分类专栏： FPGA/MATLAB精品资源专栏文章标签： matlab 16PSK LDPC

本文链接：https://blog.csdn.net/ccsss22/article/details/147231395

版权

FPGA/MATLAB精品资源专栏专栏收录该内容

63 篇文章

订阅专栏

1. 16PSK调制原理

在数字调制中，我们将二进制数字序列映射到信号的幅度、相位或频率等参数上。对于16PSK调制，我们主要是将二进制数据映射到信号的相位上。

16PSK将每4位二进制数据映射为8PSK星座图中的一个相位点，16PSK星座图通常将圆周等分为16个相位区间，每个区间对应一个唯一的4位二进制码。假设输入的比特序列为b0b1b2b3，则对应的16PSK符号的相位取值如下：

然后，将这些相位调制到载波上，得到已调信号s(t)，其数学表达式为：

其中Es是每个符号的能量，Ts是符号周期，ωc是载波角频率。这种调制方式在频域上表现为将基带信号频谱搬移到载波频率附近，从而实现信号在信道中的有效传输。

2. 16PSK解调原理

16PSK解调的目标是从接收到的已调信号中还原出原始的二进制数据。一般采用相干解调方法，其原理基于信号的相位相干性。首先，对接收到的信号r(t)与本地载波cos(ωct)和sin(ωct)进行相干解调，得到两个分量I(t)和Q(t)：

然后，对I(t)和Q(t)进行采样和判决。通过计算I和Q的幅度和相位，根据事先设定的相位判决门限，确定接收到的符号的相位。例如，若I和Q经过计算得到的相位在[0,8π)范围内，则判决接收到的符号对应的二进制数据为 0000 。再通过映射关系的逆变换得到原始的二进制数据。相干解调要求本地载波与接收信号载波同频同相，否则会引入相位误差，影响解调性能。在实际应用中，常采用锁相环（PLL）等技术来实现载波同步。

3.LDPC编译码

LDPC码作为一种前向纠错码，具有卓越的性能，其纠错能力能够接近香农极限。这意味着在理论上，LDPC码能够在极低的信噪比条件下实现可靠的数据传输，大大提高了通信系统的效率和可靠性。在深空通信中，由于信号传输距离极远，信号强度会随着距离的增加而急剧衰减，导致信噪比极低。LDPC码的应用能够在这种恶劣的信道条件下，有效地纠正传输过程中产生的错误，确保数据的准确传输。

LDPC码的校验矩阵具有稀疏性，这是其区别于其他编码的重要特性之一。稀疏校验矩阵意味着矩阵中大部分元素为零，只有少数元素为非零值。这种稀疏性使得 LDPC 码在编码和解码过程中具有较低的复杂度，因为在矩阵运算中，与零元素的运算可以省略，从而减少了计算量和存储需求。与一些传统的编码方式相比，如卷积码，其校验矩阵相对密集，在处理长码长时，计算复杂度会显著增加，而LDPC码的稀疏校验矩阵则能够有效地避免这一问题，使得在处理长码长数据时仍能保持较低的计算复杂度。

整个基于16PSK 调制解调+LDPC编译码的通信链路系统框图如下：

发送端：

1.首先是信源，产生待传输的二进制数据序列。

2.然后进入 LDPC 编码器，根据 LDPC 码的编码规则将信息序列编码为码字，增加冗余信息以提高纠错能力。

3.编码后的码字经过 8PSK 调制器，将每个码字符号映射到 8PSK 的相位上，生成 8PSK 已调信号。

4.最后通过信道发送出去。

接收端：

1.接收到经过信道传输的信号后，首先进入 8PSK 解调器，通过相干解调等方法将接收到的信号解调出原始的符号序列。

2.解调后的符号序列送入 LDPC 译码器，利用 BP 算法进行译码，尝试恢复出原始的信息序列。

3.译码后的信息序列作为信宿的输入，完成通信过程。

4.MATLAB程序

67..........................................................
%判决
yod     = [];
for i=1:Num
   
    tmps1 = yfilter1(4*Nsamp*(i-1)+Nsamp:4*Nsamp*i-Nsamp);
    tmps2 = yfilter2(4*Nsamp*(i-1)+Nsamp:4*Nsamp*i-Nsamp);
    
    X1    = mean(tmps1);
    Y1    = mean(tmps2);

    dist0 = sqrt((X1-real(sa0))^2 + (Y1-imag(sa0))^2);
    dist1 = sqrt((X1-real(sa1))^2 + (Y1-imag(sa1))^2);
    dist2 = sqrt((X1-real(sa2))^2 + (Y1-imag(sa2))^2);
    dist3 = sqrt((X1-real(sa3))^2 + (Y1-imag(sa3))^2);
    dist4 = sqrt((X1-real(sa4))^2 + (Y1-imag(sa4))^2);
    dist5 = sqrt((X1-real(sa5))^2 + (Y1-imag(sa5))^2);
    dist6 = sqrt((X1-real(sa6))^2 + (Y1-imag(sa6))^2);
    dist7 = sqrt((X1-real(sa7))^2 + (Y1-imag(sa7))^2);

    dist8 = sqrt((X1-real(sa8))^2  + (Y1-imag(sa8))^2);
    dist9 = sqrt((X1-real(sa9))^2  + (Y1-imag(sa9))^2);
    dist10= sqrt((X1-real(sa10))^2 + (Y1-imag(sa10))^2);
    dist11= sqrt((X1-real(sa11))^2 + (Y1-imag(sa11))^2);
    dist12= sqrt((X1-real(sa12))^2 + (Y1-imag(sa12))^2);
    dist13= sqrt((X1-real(sa13))^2 + (Y1-imag(sa13))^2);
    dist14= sqrt((X1-real(sa14))^2 + (Y1-imag(sa14))^2);
    dist15= sqrt((X1-real(sa15))^2 + (Y1-imag(sa15))^2);
[VV,II]=min([dist0,dist1,dist2,dist3,dist4,dist5,dist6,dist7,dist8,dist9,dist10,dist11,dist12,dist13,dist14,dist15]);

    yod    = [yod,II-1];



end
yod2=func_dec2bin(yod);

sigma = sqrt(1./(10^(SNR(ij2)/20)*R));  
z_hat = func_Dec(2*yod2-1,sigma,H,max_iter);
x_hat = z_hat(size(G,2)+1-size(G,1):size(G,2));

err(ij2,kk) = 1-length(find(bits0(1:end)==x_hat(1:end)'))/length(x_hat(1:end));

end
end


figure;
semilogy(SNR,mean(err,2),'-b^',...
    'LineWidth',1,...
    'MarkerSize',6,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.2,0.9,0.5]);
grid on
xlabel('SNR');
ylabel('error');
title('16PSK+LDPC调制解调误码率曲线');

if max_iter==2
save R21.mat SNR err
end
if max_iter==3
save R22.mat SNR err
end
if max_iter==30
save R2.mat SNR err
end

5.仿真结果

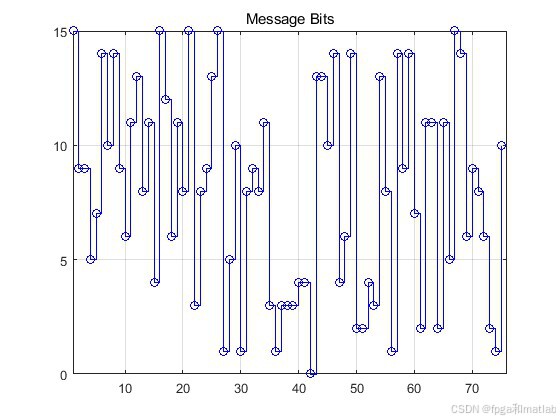
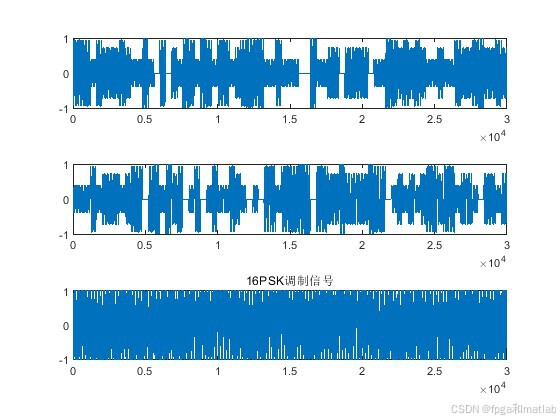
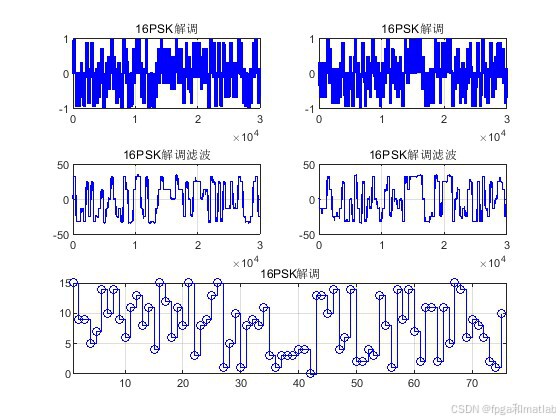
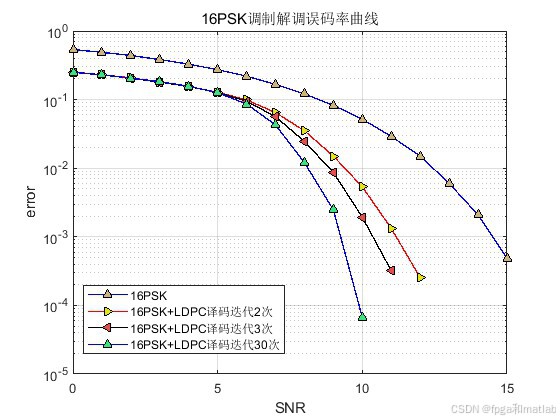
16PSK调制解调结合LDPC编译码可以在一定程度上提高通信系统的误码性能。LDPC码具有良好的纠错能力，能够纠正信道传输中引入的错误，从而降低误码率。16PSK调制在频谱效率和误码性能之间有一定的折衷，相比于BPSK等调制方式，其频谱效率更高，但误码性能相对较差。通过 LDPC 编码的纠错作用，可以弥补16PSK 调制在误码性能方面的不足。