目录
在光纤通信系统向超高速、大容量、长距离方向演进的过程中,正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)与超高阶正交振幅调制(Quadrature Amplitude Modulation, QAM)的结合是核心技术突破之一。超高阶QAM(256QAM及以上)通过在单个载波符号上承载更多比特信息,大幅提升频谱效率;OFDM则通过将高速数据流分配到多个正交子载波上并行传输,有效抵抗光纤信道的色散和非线性损伤。
1.光纤通信OFDM的优势
OFDM是一种多载波调制技术,其核心思想是将高速串行数据流分解为若干低速并行子数据流,分别调制到相互正交的子载波上传输。正交性是OFDM的关键特性,它使得子载波之间即使频谱重叠也不会产生干扰,从而大幅提升频谱利用率。在光纤通信中,OFDM的优势体现在:
1.抗色散能力强:低速子载波的符号周期远大于光纤色散引起的脉冲展宽时间,可有效抑制码间串扰。
2.灵活的资源分配:可根据信道条件动态调整各子载波的调制阶数和功率,实现自适应传输。
3.易于与超高阶QAM结合:每个子载波均可独立采用超高阶QAM调制,最大化单载波比特承载量。
2.超高阶QAM调制原理
QAM是一种幅度和相位联合调制的技术,其星座图由复平面上的离散点组成,每个星座点对应一组二进制比特流。超高阶QAM(调制阶数M≥256)的核心是通过增加星座点数量提升频谱效率,其调制阶数M与每符号比特数k的关系为:

不同阶数超高阶QAM的比特承载能力如下表所示:
| 调制阶数M | 每符号比特数k=log2M | 星座图特征 | 频谱效率提升倍数(相对 16QAM) |
|---|---|---|---|
| 256QAM | 8 | 16×16 矩形星座 | 2 倍 |
| 512QAM | 9 | 混合星座(如 32×16 + 扩展点) | 2.25 倍 |
| 1024QAM | 10 | 32×32 矩形星座 | 2.5 倍 |
| 2048QAM | 11 | 混合星座(如 64×32 + 扩展点) | 2.75 倍 |
| 4096QAM | 12 | 64×64 矩形星座 | 3 倍 |
超高阶QAM的关键挑战在于星座点间距缩小,导致系统对噪声、非线性失真和相位噪声的敏感度显著提升。因此,在光纤通信中,超高阶QAM-OFDM必须结合信道编码、均衡算法和非线性补偿技术,才能保证传输可靠性。
3.超高阶QAM-OFDM光纤通信发射端
发送端的核心任务是将原始二进制数据流转换为适合光纤传输的超高阶QAM-OFDM时域信号,具体步骤包括:信源编码→星座映射→串并转换→IFFT 变换→循环前缀插入→数模转换。
信源编码与交织

超高阶QAM星座映射
星座映射是将编码后的二进制比特流转换为复平面上的星座点。对于M阶QAM,每个星座点对应k=log2M个比特。以矩形星座为例,其星座点坐标可表示为:

对于非平方数的超高阶QAM(如512QAM、2048QAM),通常采用混合星座,其星座点由主星座(如 32×16)和扩展星座点组成,映射规则需满足格雷编码,即相邻星座点的比特汉明距离为1,以降低误码率。
串并转换与子载波分配

子载波分配需遵循正交性原则,通常选择部分子载波作为有效子载波(传输数据),其余作为保护子载波(抑制带外辐射)。设有效子载波索引为k∈[k1,k2] ,则保护子载波的调制符号为0。
IFFT
IFFT是OFDM调制的核心步骤,其作用是将频域的子载波符号转换为时域的OFDM符号。对于N点IFFT,时域信号{s(t)}的离散形式为:

循环前缀插入
循环前缀是将OFDM符号的后Ncp个采样点复制到符号前端,形成长度为N+Ncp的时域符号。CP 的长度需大于光纤信道的最大色散时延扩展τmax,以消除码间串扰和子载波间干扰。插入CP后的时域符号为:
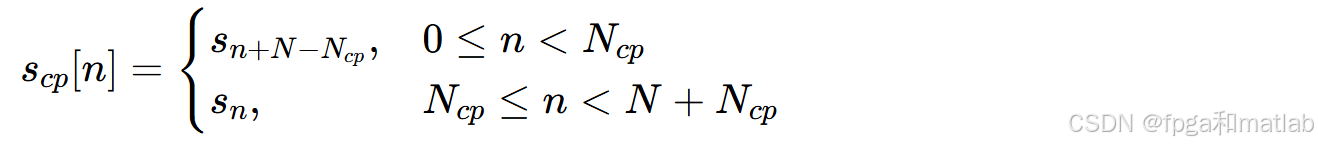
数模转换与电光调制
将离散时域信号scp[n]通过数模转换器(DAC)转换为模拟信号,再通过电光调制器(EOM)将电信号加载到光载波上,生成光OFDM信号送入光纤传输。光载波的电场表达式为:

4.光纤信道
光纤信道对光信号的影响包括线性损伤和非线性损伤,其数学模型可表示为线性传输矩阵与非线性扰动的叠加。线性损伤主要包括色度色散(CD)和偏振模色散(PMD)。

非线性损伤是超高阶QAM-OFDM系统的主要限制因素,包括自相位调制(SPM)、交叉相位调制(XPM)、四波混频(FWM)。其数学模型基于非线性薛定谔方程(NLSE):
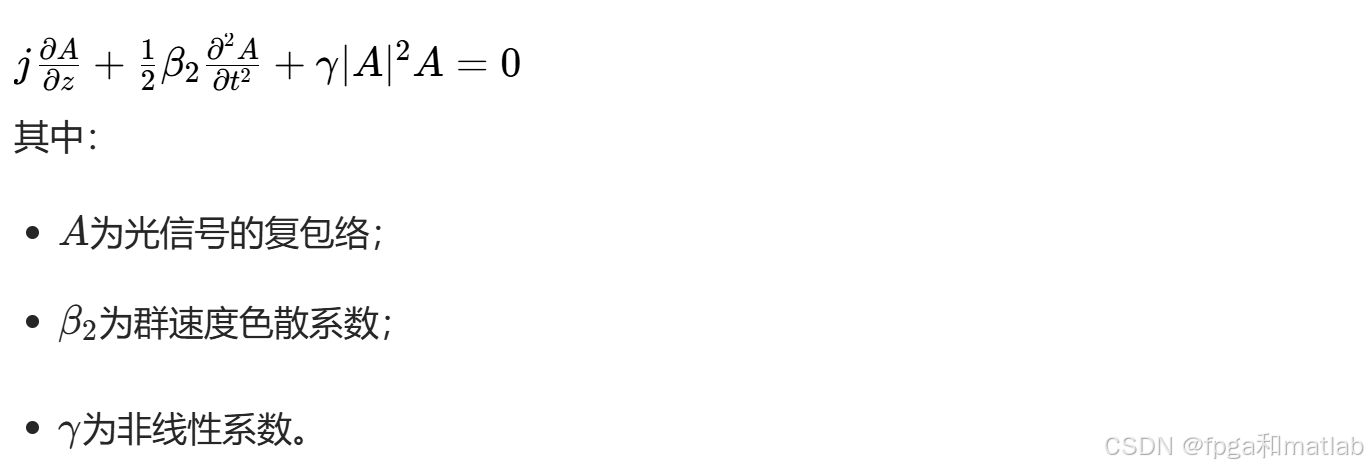
对于多载波OFDM系统,XPM和FWM的影响更为显著,需通过数字信号处理算法进行补偿。
5.超高阶QAM-OFDM光纤通信接收端
接收端的核心任务是消除信道损伤,恢复原始数据流,具体步骤包括:光电转换→模数转换→CP去除→FFT变换→信道均衡→QAM解调→解码。
其中超高阶QAM解调将均衡后的频域符号X^k映射回二进制比特流的过程。解调采用最小欧氏距离准则:

由于超高阶QAM的星座点间距小,解调过程需结合软判决信息,即计算每个比特的对数似然比:
![]()
其中bm为第m个比特,s0和s1分别为bm=0和bm=1对应的星座点集合,N0为噪声功率谱密度。
6.matlab程序与仿真测试
%% 超高阶QAM星座图生成仿真程序
% 作者:科研仿真专用
% 功能:生成256/512/1024/2048/4096QAM五种格式的星座图
clc; clear; close all;
% 1. 定义调制阶数和星座图参数
M_list = [64,256, 1024, 4096]; % 目标调制阶数
k_list = log2(M_list); % 每符号比特数
figure('Color','white','Position',[100,100,1200,800]); % 创建画布
for idx = 1:length(M_list)
M = M_list(idx);
k = k_list(idx);
% 2. 生成不同阶数QAM的星座点
if mod(sqrt(M),1) == 0 % 平方阶QAM:256/1024/4096
L = sqrt(M); % 星座图边长(偶数)
x = linspace(-L+1, L-1, L);
[X,Y] = meshgrid(x,x);
constellation = X(:) + 1j*Y(:); % 生成矩形星座
end
% 3. 星座点功率归一化(保证平均功率为1)
constellation = constellation / sqrt(mean(abs(constellation).^2));
figure(1);
% 4. 绘制星座图子图
subplot(2,2,idx);
scatter(real(constellation), imag(constellation), 10, 'b', 'filled');
grid on;
axis equal;
title([num2str(M) 'QAM星座图 (每符号' num2str(k) 'bit)'], 'FontSize',12);
xlabel('同相分量(I)');
ylabel('正交分量(Q)');
xlim([-1.5, 1.5]);
ylim([-1.5, 1.5]);
% 调整子图间距
sgtitle('超高阶QAM星座图仿真结果', 'FontSize',16, 'FontWeight','bold');
set(gcf, 'Position', [100, 100, 1200, 800]);
saveas(gcf, '超高阶QAM星座图.png'); % 保存星座图
% 2. 光纤信道参数
L = 80; % 光纤长度(km)
D = 16; % 色度色散系数(ps/(nm·km))
lambda = 1550; % 光波长(nm)
c = 3e8; % 真空中光速(m/s)
gamma = 0.3; % 非线性系数(W^-1·km^-1)
beta2 = -(D * lambda^2) / (2 * pi * c * 1e-9); % 群速度色散系数(s^2/m),转换为m单位
n_sp = 1.5; % 自发辐射因子
h = 6.626e-34; % 普朗克常数(J·s)
nu = c / (lambda * 1e-9); % 光频率(Hz)
G = 10; % 光纤放大器增益(倍)
SNR = 45; % 接收端信噪比(dB)
sig_rx = fiber_channel(constellation, L, beta2, gamma, n_sp, h, nu, G, SNR);
figure(2);
subplot(2,2,idx);
plot(real(sig_rx), imag(sig_rx), '.');
grid on;
axis equal;
title([num2str(M) 'QAM星座图 (每符号' num2str(k) 'bit)'], 'FontSize',12);
xlabel('同相分量(I)');
ylabel('正交分量(Q)');
end
% 2. 光纤信道传输函数(含线性+非线性损伤+噪声)
function sig_rx = fiber_channel(sig_tx, L, beta2, gamma, n_sp, h, nu, G, SNR)
% 2.1 线性损伤:色度色散(频域处理)
N = length(sig_tx);
f = [(-N/2 : N/2 - 1) / N]'; % 归一化频率
% 色度色散频域传输函数
H_CD = exp(1j * beta2 * (2 * pi * f).^2 * L * 1000); % L转换为m
sig_tx_freq = fftshift(fft(sig_tx));
sig_cd_freq = sig_tx_freq .* H_CD;
sig_cd = ifft(ifftshift(sig_cd_freq));
% 2.2 非线性损伤:自相位调制(SPM)(时域处理)
% 简化SPM模型:相位偏移与信号功率成正比
P_avg = mean(abs(sig_cd).^2); % 平均功率
phi_spm = gamma * P_avg * L * 1000; % SPM相位偏移
sig_nonlinear = sig_cd .* exp(1j * phi_spm);
% 2.3 噪声叠加:ASE噪声(基于信噪比计算)
sig_power = mean2(abs(sig_nonlinear).^2);
noise_power = sig_power / (10^(SNR/10)); % 噪声功率
% 生成复高斯噪声(同相/正交分量独立)
noise = sqrt(noise_power / 2) * (randn(N, 1) + 1j * randn(N, 1));
% 叠加ASE噪声
sig_rx = sig_nonlinear + noise;
end测试结果如下图所示:
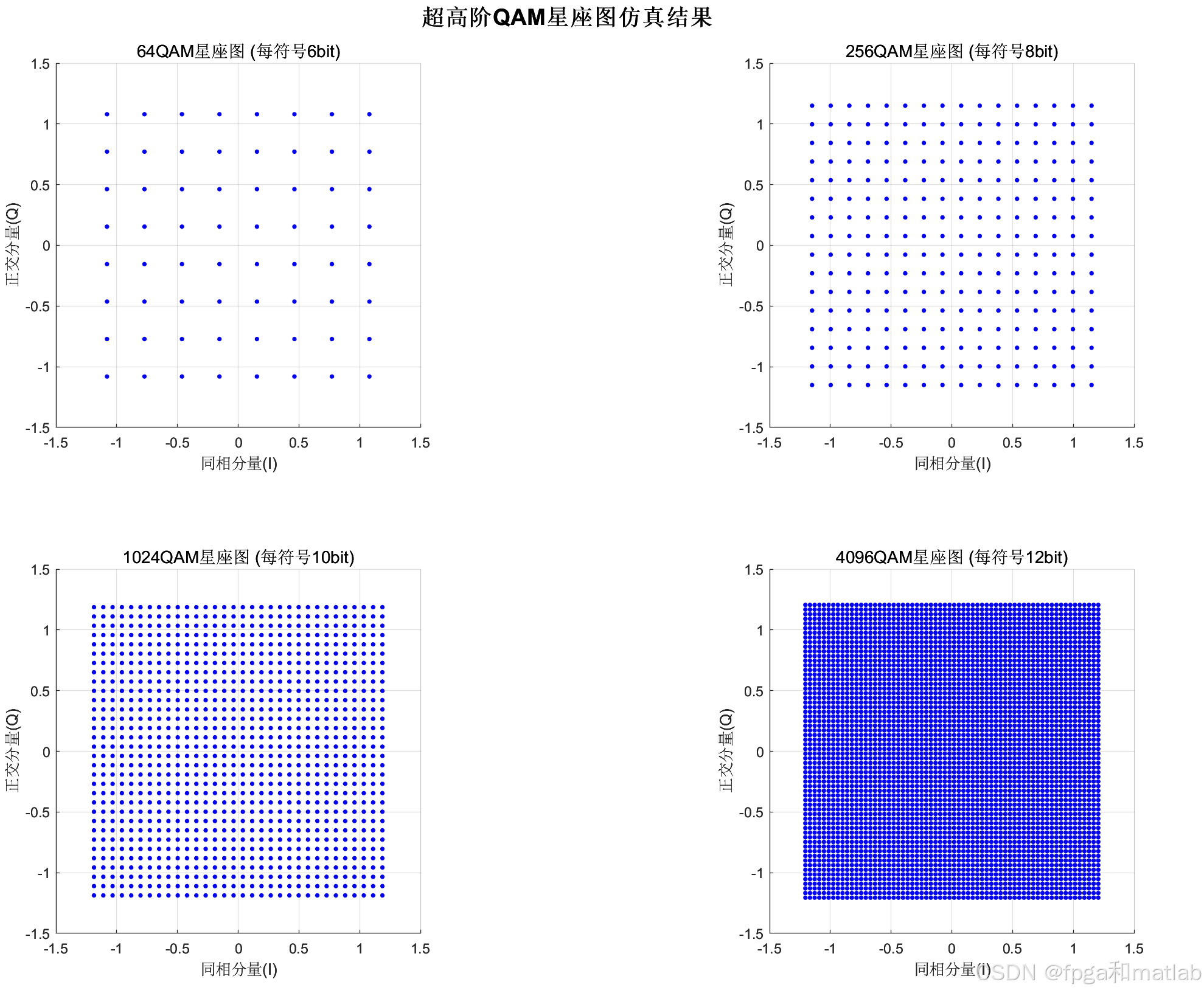
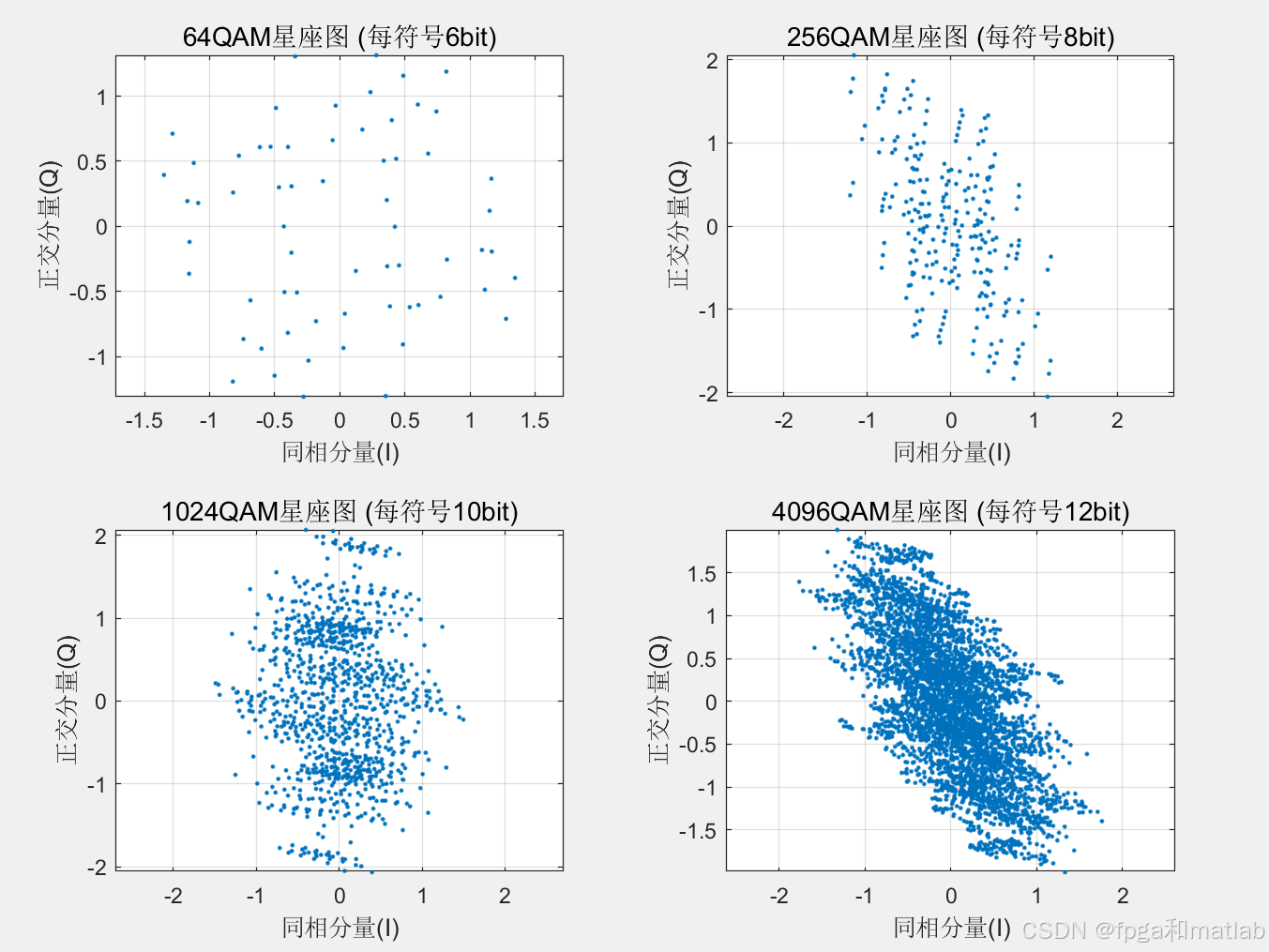
通过光纤信道之后,星座图变为:
























 1172
1172

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










