一、滑模控制
滑模变结构控制理论是由俄罗斯学者Emelyanov提出,Utkin等人倡导的一种特殊的非线性控制理论。
考虑非线性系统
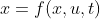
其中, ,
,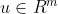 ,
, 。选取滑模函数
。选取滑模函数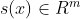 。并寻求控制
。并寻求控制
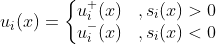
使得:
(1)滑模面(即滑模函数 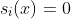 的超平面)以外的相轨迹于有限时间内到达滑模面。这称之为到达条件,即满足:
的超平面)以外的相轨迹于有限时间内到达滑模面。这称之为到达条件,即满足:
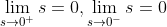
此时系统的运动称之为趋近运动或趋近模态。
(2)滑模面上降阶系统(当系统处于滑模面上,系统此时阶次降低,因而简称降阶系统)的运动渐近稳定,动态品质好。此时系统的运动称之为滑动模态。这种通过切换控制迫使系统产生一种具有良好动态品质的滑动模态运动的控制系统,称为滑动模态变结构控制系统,简称滑模控制系统。

























 6354
6354

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










