06、姿态解算---欧拉角推导

keaishamao

于 2024-04-26 13:46:55 发布

阅读量447

点赞数 8

分类专栏：姿态解算文章标签：人工智能

本文链接：https://blog.csdn.net/keaishamao/article/details/138213987

版权

姿态解算专栏收录该内容

7 篇文章 1 订阅

订阅专栏

1、概率

以MPU规定的坐标作为公式推导的地理坐标系和起始物体坐标系。将芯片水平放置，以芯片内部中心为原点，水平向右为X轴，竖直向上为Z轴，指向正前方为Y轴：

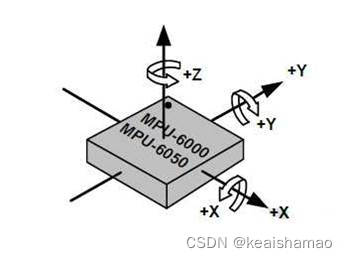
求物体的姿态角(在地面看物体运动)时，物体旋转过后相对于之前的角度变化信息可以等效为物体依次绕三个轴旋转复合得到，规定绕z轴旋转称物体的航向角(ψ)、绕y轴旋转称物体的俯仰角(γ)、绕x轴旋转称物体的翻滚角(θ),下面先推导物体分别绕三个轴的变换矩阵，最后根据三个变换矩阵复合得到物体相对于地理坐标系的角度信息。

2、物体绕Z轴旋转

物体绕z轴旋转，可知z轴不变，x、y轴的变换关系如下图所示：

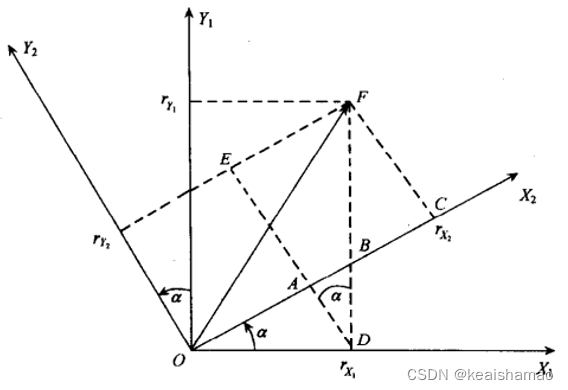
由图可知：

$r_{x2}=OA+AB+BC=ODcos\alpha +BDsin\alpha +BFsin\alpha$

$=r_{x1}cos\alpha +r_{y1}sin\alpha$

$r_{Y2}=DE-AD=DFcos\alpha -ODsin\alpha$

$=r_{y1}cos\alpha -r_{x1}sin\alpha$

$r_{z2}=r_{z1}$

将以上三式写成矩阵形式，则得到绕z轴旋转α角度后的坐标关系如下：

$\begin{bmatrix} r_{x2}\\ r_{y2}\\ r_{z2} \end{bmatrix}=\begin{bmatrix} cos\alpha & sin\alpha &0 \\ -sin\alpha &cos\alpha & 0\\ 0& 0 & 1 \end{bmatrix}\begin{bmatrix} r_{x1}\\ r_{y1}\\ r_{z1} \end{bmatrix}$

3、物体绕y轴旋转

物体绕Y轴旋转，可知Y轴不变，x、z轴的变换关系如下图所示：

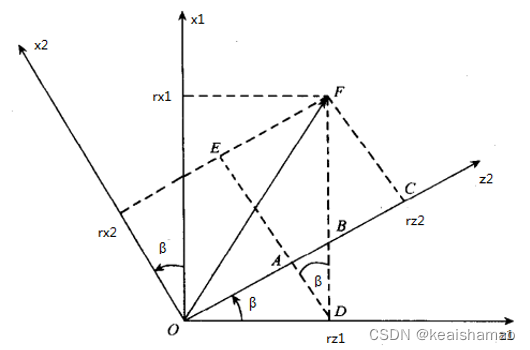
由图可知：

$r_{x2}=DE-AD=DFcos\beta -ODsin\beta$

$=r_{x1}cos\beta -r_{z1}sin\beta$

$r_{y2}=r_{y1}$

$r_{z2}=OA+AB+BC=ODcos\beta +BDsin\beta +BFsin\beta$

$=r_{z2}cos\beta +r_{x1}sin\beta$

将以上三式写为矩阵形式，则得到物体绕y轴旋转β角度后的坐标关系：

$\begin{bmatrix} r_{x2}\\ r_{y2}\\ r_{z2} \end{bmatrix}=\begin{bmatrix} cos\beta & 0 & -sin\beta \\ 0& 1& 0\\ sin\beta&0 &cos\beta \end{bmatrix}\begin{bmatrix} r_{x1}\\ r_{y1}\\ r_{z1} \end{bmatrix}$

4、物体绕x轴旋转

物体绕x轴旋转，可知x轴不变，y、z轴的变换关系如下图所示：

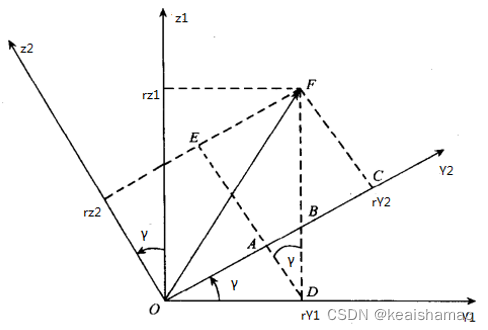
由图可知：

$r_{x2}=r_{x1}$

$r_{y2}=OA+AB+BC=ODcos\gamma +BDsin\gamma +BFsin\gamma$

$=r_{y1}cos\gamma +r_{z1}sin\gamma$

$r_{z2}=DE-AD=DFcos\gamma -ODsin\gamma$

$=r_{z2}cos\gamma -r_{y1}sin\gamma$

将以上三式写为矩阵形式，则得物体绕x轴旋转γ角度后的坐标关系：

$\begin{bmatrix} r_{x2}\\ r_{y2}\\ r_{z2} \end{bmatrix}=\begin{bmatrix} 1 & 0& 0\\ 0 &cos\gamma & sin\gamma \\ 0& -sin\gamma & cos\gamma \end{bmatrix}\begin{bmatrix} r_{x1}\\ r_{y1}\\ r_{z1} \end{bmatrix}$

5、旋转矩阵

上面推导了物体分别绕三个轴旋转的变换矩阵，求一个物体的姿态角时，可以等效为物体绕三个轴旋转的复合。规定绕z轴旋转称为物体的航向角 $\varphi$ ，绕y轴旋转称为物体的俯仰角 $\gamma$ ，绕x轴旋转称为物体的翻滚角 $\theta$ 。符合后的姿态矩阵为 $C_{E}^{b}$ 。在旋转时有多种旋转方法，这里取旋转顺序为Z-Y-X，则得到的旋转矩阵为：

$C_{E}^{b}=\begin{bmatrix} 1 &0 &0 \\ 0 & cos\theta & sin\theta\\ 0&-sin\theta &cos\theta \end{bmatrix}\begin{bmatrix} cos\gamma &0 &-sin\gamma \\ 0& 1 & 0\\ sin\gamma &0 & cos\gamma \end{bmatrix}\begin{bmatrix} cos\varphi & sin\varphi &0 \\ -sin\varphi &cos\varphi &0 \\ 0& 0 & 1 \end{bmatrix}$

$=\begin{bmatrix} cos\gamma cos\varphi &cos\gamma sin\varphi &-sin\gamma \\ sin\theta sin\gamma cos\varphi &sin\theta sin\gamma sin\varphi +cos\theta cos\varphi &sin\theta cos\gamma \\ cos\theta sin\gamma cos\varphi +sin\theta sin\varphi & cos\theta sin\gamma sin\varphi -sin\theta cos\varphi & cos\theta cos\gamma \end{bmatrix}$