【深度好文】严格正确的评分规则、预测和估计

摘要

评分规则通过根据预测分布和实现的事件或价值分配数值分数来评估概率预测的质量。如果预测者将从分布中得出的观察值的期望分数最大化，那么评分规则是合适的，如果他或她发布概率预测F，而不是G。如果最大值是唯一的，它是严格正确的。在预测问题中，适当的评分规则鼓励预测者做出仔细的评估并保持诚实。在估计问题中，严格的适当评分规则提供了有吸引力的损失和效用函数，可以根据手头的问题进行调整。本文回顾和发展了一般概率空间上的适当评分规则理论，并提出和讨论了相应的例子。

适当的评分规则来源于凸函数，并与信息度量、熵函数和Bregman散度相关。在分类变量的情况下，我们证明了Savage表示的严格版本。以预测密度的形式为概率预测打分规则的例子包括对数、球面、伪球面和二次得分。连续排序概率分数适用于采用预测累积分布函数形式的概率预测。它概括了绝对误差，并形成了一种新的、非常普遍的分数类型——能量分数的特例。像许多其他评分规则一样，能量评分在单变量和多变量设置中都承认以负确定函数表示的核表示，与Hoeffding类型的不等式相关联。还讨论了分位数和区间预测的适当评分规则。我们将适当的评分规则与贝叶斯因子和交叉验证联系起来，并提出一种新的交叉验证形式，称为随机交叉验证。对北美太平洋西北地区概率天气预报的一个案例研究说明了适当的重要性。我们注意到点和量值估计的最佳得分方法，并提出直观吸引人的区间得分作为区间估计中的效用函数，解决了宽度和覆盖率。

简介

统计分析的一个主要目的是对未来作出预测，并对与之相关的不确定性提供适当的度量。因此，预测本质上应该是概率性的，采取概率分布的形式——未来数量或事件的分布(david 1984)。事实上，在过去的二十年中，概率预测在天气和气候预测等应用中已经成为常规(Palmer 2002;Gneiting and Raftery 2005)，计算金融学(Duffie and Pan 1997)和宏观经济预测(Garratt, Lee, Pesaran, and Shin 2003;格兰杰2006)。在统计文献中，马尔科夫链蒙特卡罗方法的进步(参见，例如，Besag, Green, Higdon和Mengersen 1995)导致预测分布的使用爆炸式增长，主要以蒙特卡罗样本的形式来自感兴趣数量的后一预测分布。在早期的工作中(Gneiting, ratry, Balabdaoui, and Westveld 2003;Gneiting, Balabdaoui, and ratry 2006)，我们认为概率预测的目标是最大限度地提高校准后预测分布的清晰度。校准是指分布预测与观测值之间的统计一致性，是预测与实际发生的事件或值的共同属性。锐度是指预测分布的集中程度，只是预测的一种属性。

评分规则通过根据预测分布和实现的事件或值分配数值分数，为概率预测的评估提供了汇总度量。在启发方面，评分规则的作用是鼓励评估者认真评估并诚实(Garthwaite, Kadane, and O 'Hagan 2005)。在评估方面，评分规则衡量概率预测的质量，奖励预测工作的概率评估者，并对竞争预测程序进行排名。气象学家将这一广泛的任务称为预报验证，许多潜在的方法是由大气科学家开发的(Jolliffe和Stephenson 2003)。在贝叶斯语境中，分数通常被称为效用，强调贝叶斯原则最大化预测分布的预期效用(Bernardo and Smith 1994)。我们将评分规则视为正向奖励，预测者希望最大化这种奖励。具体来说,如果预报员引号预测分布P和事件x实现,那么他或她的奖励(P, x),函数年代(P·)值的实线或扩展的实线R =(−∞,∞),和我们写年代(P, Q)年代的期望值(P·)问:假设下,然后,预报员的最佳判断是distri——butional Q.The预报员预测没有动力去预测P ? = Q和鼓励引用他或她真正的信仰,当且仅当P = Q时，当S(Q, Q)≥S(P, Q)且相等时，P = Q。

在估计问题中，严格适当的评分规则提供了有吸引力的损失和效用函数，可以为科学问题量身定制。为了确定这个想法，假设我们希望拟合基于样本X1的参数化模型Pθ，…对于极值θ，我们可以用均值来衡量拟合优度

其中S是一个严格正确的评分规则。如果θ表示真参数值，则渐近参数表明arg maxθ Sn(θ)→θ0为n→∞。这就提出了一种通用的估计方法:根据当前问题选择一个严格合适的评分规则，并使用θn = arg maxθ Sn(θ)作为基于评分规则的最佳评分估计器。Pfan- zagl(1969)和birg<s:1>和Massart(1993)在最小对比度估计的标题下研究了这种方法。最大似然估计是最优分数es-估计的一种特殊情况，最优分数估计是m -估计的一种特殊情况(Huber 1964)，所要优化的函数来源于一个严格合适的评分规则。

本文回顾和发展了一般概率空间的适当评分规则理论，提出并讨论了其中的例子，并给出了案例研究。本文的其余部分组织如下。在第2节中，我们陈述了一个基本的表征定理，回顾了适当的评分规则、信息度量、熵函数和Bregman散度之间的联系，并介绍了技能分数。在第3节中，我们转向分类变量的评分规则。我们证明了Savage(1971)表示的一个严格版本，并涉及到Schervish(1989)最近的一个特征，该特征适用于二分类事件的概率预测。Bremnes (2004, p. 346)指出，连续变量概率预测的评分规则的文献是稀疏的。我们将在第4节中讨论这个问题，其中我们将讨论球面、伪球面、对数和二次分数。

连续排序概率分数是近年来备受关注的一种方法，它具有很好的性质，可以作为评价实值变量概率预测的标准分数。它形成了一种特殊的情况，一种新颖的，非常普遍的评分规则，能量评分。在第5节中，我们介绍了一个更一般的结构，基于负定函数和Hoeffd类型的不等式产生核分数，并附带了期望不等式和正定函数的结果。在第6节中，我们研究了分位数和区间预测的评分规则。我们证明了分位数预测的适当评分规则的类别比Cervera和Muñoz(1996)推测的要大，并讨论了区间评分，预测区间评分规则是适当的，具有直观的吸引力。在第7节中，我们将适当的评分规则与贝叶斯因子和交叉验证联系起来，并提出一种新的交叉验证形式，称为随机交叉验证。在第8节中，我们提出了在概率天气预报评估中使用评分规则的案例研究。在第9节中，我们转向最优分数估计。

如果样本空间是有限的，并且熵函数足够光滑，那么散度函数就变成了Breg- man散度(Bregman 1967)，与凸函数G.Bregman散度相关联。Bregman散度在优化中起着重要作用，最近引起了机器学习社区的注意(Collins, Schapire, and Singer 2002)。虽然d(P, Q)不一定与d(Q, P)相同，但我们也使用了Bregman距离这个术语。

一个有趣的问题是找到散度函数d是分数散度的条件，在这个意义上，它允许一个适当的评分规则S的表示(7)，并描述找到这样一个评分规则的原则方法。Savage(1971)的划时代工作提供了对称散度函数d是分数散度函数的必要条件:如果P和Q集中在相同的两个互斥事件上，并由各自的概率P, Q∈[0,1]确定，则d(P, Q)约化为(P−Q) 2的线性函数。david(1998)指出，如果d是一个分数收敛，那么d(P, Q)−d(P?， Q)是Q对所有P的仿射函数，P?∈P，并证明了部分逆。

适当的评分规则在统计决策问题中自然出现(david 1998)。给定一个结果空间和一个动作空间，设U(ω， a)为结果ω和动作a的效用，设P为结果空间上概率测度的凸类。设aP表示P∈P的贝叶斯行为，则得分规则

在实践中，分数是汇总的，相互竞争的预测程序根据平均分数进行排名，

相互竞争的预测程序的分数，如果它们指的是完全相同的一组预测情况，则直接具有可比性。如果要比较不同情况下的得分，那么必须相当小心地将内在可预测性和预测性绩效的共同影响区分开来。例如，在天气和气候要素的可预测性方面存在着大量的空间和速度变化(Langland et al. 1999;Campbell and Diebold 2005)。因此，在特定地点或季节中得分较高的游戏可能在其他地点或季节中得分较低，反之亦然。为了解决这个问题，大气科学家提出了这种形式的技能分数

技能分数标准化为(8)取1为最优预测值，最优预测值通常被理解为实现的事件或价值中的一个点度量值，取0为参考预测值。技能得分为负值表明预测的质量低于参考。参考预报通常是气候预报，即对预报的边际分布的估计。例如，华盛顿州西雅图独立日最高气温的气候概率预报可能是当地7月4日最高气温历史记录的平滑版本。气象学预报是独立于预报范围的;它们是由结构校准的，但往往缺乏清晰度。

不幸的是，形式(8)的技能分数通常是不恰当的，即使基本的评分规则S是正确的。Mur- phy(1973)研究了二元事件概率预测的Brier技能分数情况下的对冲策略。他证明，Brier技能得分是渐近正确的，也就是说，随着独立预测数量的增加，对冲的好处变得可以忽略不计。类似的论点也适用于基于其他适当评分规则的技能得分。马森(2004)对Brier技能分数的适当性的主张建立在不合理的近似上，通常是不正确的。

分类变量的评分规则

我们现在回顾萨维奇(1971)和Schervish(1989)，描述了分类变量和二元变量概率预测的评分规则，并给出了适当评分规则的示例。

CRPS

对预测密度的限制通常是不切实际的。例如，概率定量降水预报涉及点质量为零的分布(krzysztoflow - icz和Sigrest 1999;Bremnes 2004)，而预测分布通常用样本来表示，可能起源于马尔科夫链蒙特卡罗。因此，根据预测累积分布函数直接定义评分规则似乎更有说服力。此外，上述分数对距离不敏感，这意味着对接近但不完全相同的值分配高概率不会给予信用。

为了解决这种情况，设P由r上的Borel概率度量组成。我们确定一个概率预测-类P的成员及其累积分布函数F，并使用标准符号表示样本空间r的元素。连续排序概率得分(CRPS)定义为

对应于相关二值概率预测在所有实值阈值处的Brier分数的积分
(Matheson and Winkler 1976;Hersbach 2000)。

由于在(20)中缺乏易于计算的积分解，CRPS的应用受到了阻碍，并且已经提出使用数值正交规则来代替(Staël von Holstein 1977;昂格尔1985)。然而，积分通常可以用封闭形式求值。根据Baringhaus and Franz(2004)的引理2.2或sz<s:1> kely and Rizzo(2005)的同一性(17)，

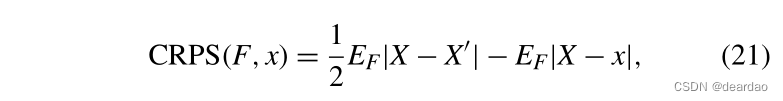
X和X在哪里?是具有分布函数F和有限一阶矩的随机变量的独立副本。如果预测分布为高斯分布，均值为µ，方差为σ2，则

其中φ和?表示标准高斯变量的概率密度函数和累积分布函数。如果预测分布采用大小为n的样本的形式，则(20)的右侧可以根据各自的阶统计量在总共O(n log n)次操作中进行评估(Hersbach 2000，第4.b节)。

CRPS相对于P类是固有的，相对于具有有限第一矩的Borel概率测度的子类P1是严格固有的。相关的期望分数函数或信息度量，

与负选择性函数相吻合(马瑟伦 1984)，相应的散度函数，

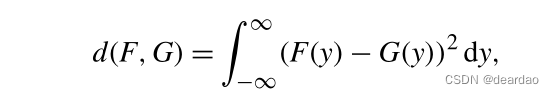
是对称的，并且是克莱姆萨-冯·米塞斯型的。

CRPS最近在大气科学界引起了新的兴趣(Hersbach 2000;Candille and Talagrand 2005;Gneiting, ratry, Westveld, and Goldman 2005;Grimit, Gneiting, Berrocal, and Johnson 2006;Wilks 2006，第302-303页)。它通常用于负方向，如CRPS * (F, x) = - CRPS(F, x)。那么表示(21)可以写成

这让我们对这个问题有了新的了解。在负方向下，CRPS可以与观测值以相同的单位报告，并且它概括了如果F是确定性预测(即点测量)，它所减少的绝对误差。因此，CRPS提供了一种比较确定性预报和概率预报的直接方法。

我们介绍了借鉴szacimkely(2003)统计能量视角的CRPS的概括。设Pβ， β∈(0,2)，表示Rm上的Borel概率测度P的类别，使得EP?X?β是有限的，其中?·?表示欧几里德范数。我们定义能量分数，

对数分数和贝叶斯因子的等价性

概率预测规则通常由概率模型生成，而比较概率模型的标准贝叶斯方法是通过贝叶斯因子。假设样本X = (X1，…)， Xn)的待预测值。假设我们有两个基于概率模型H1和H2的预测规则。到目前为止，在本文中，我们关注的是在观察到任何Xi之前完全指定预测规则的情况;也就是说，从预测的数据中不需要估计任何参数。在这种情况下，H1对H2的贝叶斯因子是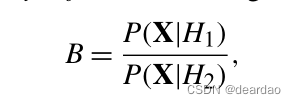
因此，如果使用对数分数，则对数贝叶斯因子是两个模型的分数之差，
Good(1952)指出了这一点，他将对数贝叶斯因子称为证据权重。它建立了两个联系:(1)在这种无参数的情况下，贝叶斯因子相当于对数分数;(2)贝叶斯因子不仅适用于参数概率模型的比较，而且更广泛地适用于任何类型的概率预测规则的比较。

到目前为止，在本文中，我们已经采取了概率预测是完全指定的，但它们往往只指定了从数据估计的未知参数。现在假设所考虑的预测规则只指定到未知参数，θk为Hk，从数据中估计。那么贝叶斯因子仍然由(50)给出，但现在P(X|Hk)是积分似然，