matlab 机器人工具箱4-机械臂逆运动学

本文主要参考清华大学出版社的《机器人仿真与编程技术》一书

本文参考 《机器人仿真与编程技术》

机器人逆运动学就是即在已知末端的工具坐标系相对于基坐标系的位姿。计算所有能够到达指定位姿的关节角。求解可能出现：

• 不存在相应解
• 存在唯一解
• 存在多解

我们把机械臂的全部求解方法分为两大类：封闭解和数值解法。数值解由于是通过迭代求解，所以它的速度会比封闭解求法慢。封闭解又可以分为代数法和几何法。

理论部分参考： https://wenku.baidu.com/view/03d586024afe04a1b171de8d.html

 

封闭解

封闭解存在的两个充分条件：

1. 三个相邻的关节轴交于一点
2. 三个相邻的关节轴互相平行

几何法

 

 

 

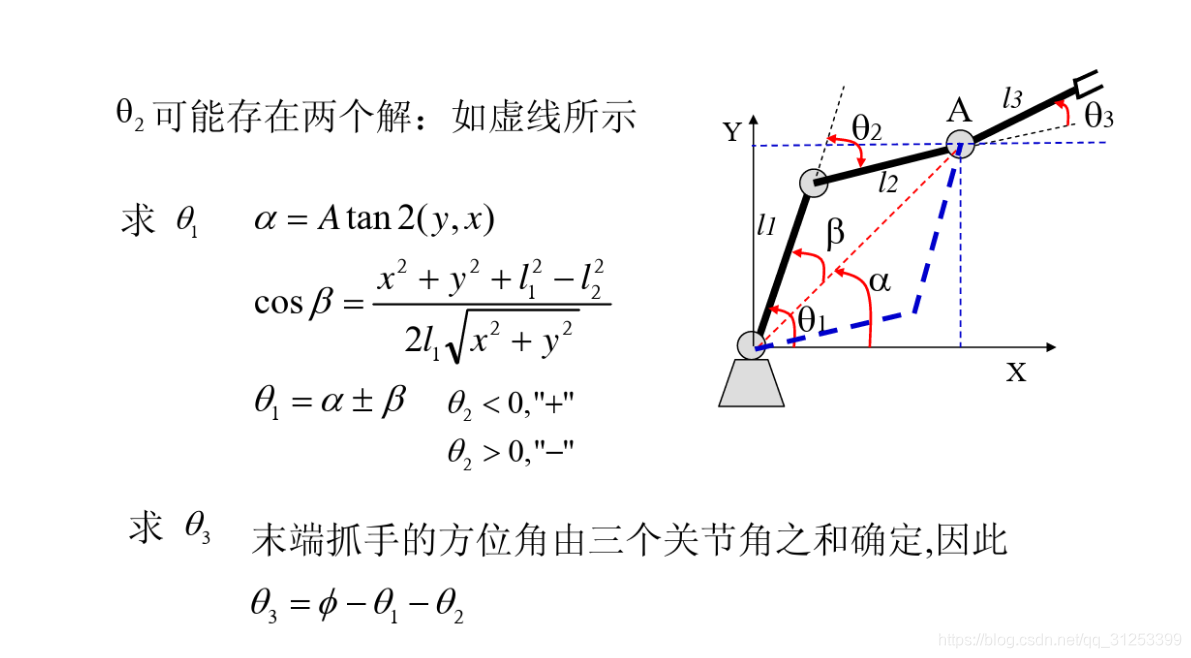
总结就是根据现在的状态，通过几何学建立各个角度之间的关系，进行求解

代数法

 

 

 

我们看到代数法就是对各坐标系的旋转齐次矩阵进行平移，每次平移一个，之后通过矩阵乘法的对应关系，得到末端的其次矩阵元素（已知）和各齐次变换矩阵参数（未知）的关系。

 

《机器人仿真与编程技术》这本书呢，给了一个 matlab 工具箱中的封装的方法：

在封闭解的方法中，使用 ikine6s() 求解逆运动学的问题，只适用于关节数为6，且腕部三旋转关节的轴交于一点的情况。相关配置参数：

 

左旋‘l’	右旋 ‘r’
肘部向上 ‘u’	肘部向下 ‘d’
腕部翻转 ‘f’	腕部不翻转 ‘n’

之后使用KUKA KR5的机器人

 mdl_KR5

会发现加载了模型：

 

查看具体的参数可以直接点击或者用命令行输入参数名进行查看

 

>> KR5
KR5 =
Kuka KR5:: 6 axis, RRRRRR, stdDH, slowRNE                        
+---+-----------+-----------+-----------+-----------+-----------+
| j |     theta |         d |         a |     alpha |    offset |
+---+-----------+-----------+-----------+-----------+-----------+
|  1|         q1|        0.4|       0.18|     1.5708|          0|
|  2|         q2|      0.135|        0.6|    3.14159|          0|
|  3|         q3|      0.135|       0.12|    -1.5708|          0|
|  4|         q4|       0.62|          0|     1.5708|          0|
|  5|         q5|          0|          0|    -1.5708|          0|
|  6|         q6|          0|          0|          0|          0|
+---+-----------+-----------+-----------+-----------+-----------+
tool:    t = (0, 0, 0.115), RPY/xyz = (0, 0, 0) deg              
之后
>> qn=[0 0 pi/4 0 pi/6 pi/3]


qn =


         0         0    0.7854         0    0.5236    1.0472


>> T=KR5.fkine(qn)


T =
    0.1294   -0.2241   -0.9659    0.3154
   -0.8660   -0.5000         0         0
   -0.4830    0.8365   -0.2588    -0.153
         0         0         0         1
>> KR5.plot(pn)

 

 

我们使用

>> KR5.ikine6s(T)


ans =


    3.1416   -3.3226    3.1775    3.1416    1.5259    1.0472

发现结果和输入的qn不一样，这就是逆解的不唯一性，效果一样但是个关节数值不一样，这个时候我们就通过指定参数来限制末端的解

>> KR5.ikine6s(T,'run')


ans =


   -0.0000         0    0.7854   -0.0000    0.5236    1.0472

这时候就得到了输入的角度值。

 

 

数值解

主要就是 牛顿-拉普森方法，我们参考： https://blog.csdn.net/libing403/article/details/89035960

并且我们解读KDL的代码的时候，也是使用 牛顿-拉普森相关的算法

matlab工具箱提供了ikine()函数求解逆运动学的问题，它适用于各种关节数目的机械臂，通过设定初始的关节角坐标对机械臂运动学配置进行隐式的控制。

正是因为用到 牛顿-拉普森的一些理念，所有参数的话不同于封闭解，需要输入猜测的解（参考值）。这个就是让使结果由猜测的解开始迭代，也就是找到离猜测值最近的逆解。这个的好处就是，我们在做轨迹规划的时候，可以使上一点作为参考值，使机械臂各关节的运动最小

mdl_puma560
qn=[0 0 pi/4 0 pi/6 pi/3]
T=p560.fkine(qn)
q1=p560.ikine(T)
q2=p560.ikine(T,[0 0 3 0 0 0])

输出的结果

q1 =
   -0.0000   -0.0000    0.7854    0.0000    0.5236    1.0472
q2 =
   -0.0000   -0.0000    0.7854    0.0000    0.5236    1.0472

可以看出q1接近0 0 0 0 0 0，q2接近0 0 3 0 0 0。