连续时间与离散时间的基于视觉的SLAM:对比研究
Giovanni Cioffi, Titus Cieslewski, 和 Davide Scaramuzza
摘要
机器人从业者通常通过离散时间公式来处理基于视觉的SLAM问题。这种方法的优势在于理论已得到巩固,并且对成功和失败的情况有很好的理解。然而,在离散时间SLAM中,当估计过程中存在来自不同传感器的高频率和/或异步测量时,往往需要定制算法和简化假设。相比之下,连续时间SLAM通常被从业者忽视,但却不受这些限制。实际上,它允许异步整合新的传感器数据,而不需要为每个新测量添加新的优化变量。这样一来,异步或高频连续的传感器数据流的整合不再需要复杂且高度工程化的算法,使多种传感器模式的融合变得直观。然而,连续时间引入了一个先验,在某些不利情况下可能会使轨迹估计效果变差。在本研究中,我们旨在系统性地比较这两种公式在基于视觉的SLAM中的优缺点。为此,我们进行了广泛的实验分析,涵盖不同的机器人类型、运动速度和传感器模式。我们的实验分析表明,无论轨迹类型如何,当传感器不同步时,连续时间SLAM优于离散时间SLAM。在本研究中,我们开发并开源了一种模块化且高效的软件架构,包含用于解决离散和连续时间SLAM问题的最新算法。
索引词-SLAM, 建图, 定位, 传感器融合。
补充材料
代码可以在这里找到:https://github.com/uzh-rpg/rpg_vision-based_slam
I. 引言
同时定位与建图(SLAM)[1] 是构建环境地图并同时估计机器人状态的问题。精确且稳健的SLAM算法是解锁自主机器人导航的关键。
(a) 在流行的SLAM方法中,通常在其中一个传感器的测量时刻(例如,基于视觉的SLAM中的相机)上离散表示状态。如果其他传感器在相同时间没有测量,则需要采用插值等技术来表达误差项。
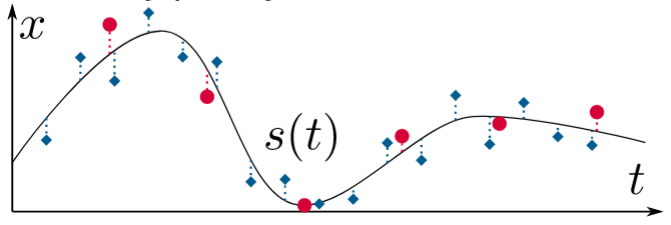
(b) 在连续时间SLAM中,估计的状态是通过连续函数来表示的,例如,样条函数
s
(
t
)
s(t)
s(t)。现在,对于任何在时刻
t
i
t_{i}
ti 的测量,可以通过将测量值与样条样本
s
(
t
i
)
s\left(t_{i}\right)
s(ti) 或其任何导数
s
′
(
t
i
)
,
s
′
′
(
t
i
)
,
…
s^{\prime}\left(t_{i}\right), s^{\prime \prime}\left(t_{i}\right), \ldots
s′(ti),s′′(ti),… 进行比较来表达有意义的误差项,例如,对于IMU测量不需要积分。

© 此外,连续时间表示允许同时估计传感器之间的时间偏移甚至漂移。为此,某个传感器的误差项可以简单地通过其测量时刻的样条加上一个常数时间偏移来表达,这个偏移在所有测量中是共享的,即 s ( t i + Δ t ) s\left(t_{i}+\Delta t\right) s(ti+Δt)。然后, Δ t \Delta t Δt 可以与 s s s 的参数一起共同优化。在这个例子中,蓝色测量值将“向左移动”。
图1:在一个简单示例中,展示了使用连续时间状态表示的好处,其中变量 x ( t ) x(t) x(t) 是从两个以不同频率测量 x x x 的噪声传感器(红点和蓝色菱形)中估计的。
在提供与定位和建图相关信息的众多传感器中,摄像头因其信息丰富、成本低、重量轻而成为非常方便的解决方案。基于视觉的SLAM算法通常使用摄像头作为主要传感器,但不一定是唯一传感器。最常见的基于视觉的SLAM公式是基于离散时间(DT)轨迹表示 [2]。即,相机的位姿在每次新测量(即图像)可用时被估计。离散时间公式的优点在于理论已非常成熟。过去几年中,已出现许多成功的应用 [1]。它的局限性已被很好理解,并且正在进行的研究中已得到解决。
尽管摄像头可以作为SLAM系统中唯一的信息源,但融合多种传感器模式对提高精度和稳健性是有益的。在离散时间SLAM中,需要定制算法来将来自不同来源的异步测量包含到估计过程中 [3]。同样,需要专门的解决方案来避免每次有新测量时都向估计问题中添加新状态 [4]。通过这种方式,可以将高频传感器纳入估计过程中,从而限制了计算复杂度的增加。
近年来,研究人员一直在探索使用连续时间(CT)表示来编码相机轨迹 [5],[6],[7]。基于连续时间的概率SLAM公式已类似于离散时间案例得出。特别是,连续时间轨迹表示的应用已用于多传感器标定 [5],[8],规划 [9],以及3D重建 [10],[11]。连续时间公式为估计问题带来了几个优点。首先,连续时间轨迹可以在任何时刻进行采样。这使得融合异步传感器和估计时间偏移变得简单,见图1。这样的特性对于具有连续数据流的传感器也很有益,例如LiDAR、滚动快门相机和事件相机。其次,连续时间公式去除了为每个传感器测量包含优化变量的需求。优化问题的计算复杂度保持在一定范围内,允许轻松地将高频传感器(如惯性测量单元(IMU))纳入估计过程中。然而,连续时间表示引入了关于轨迹光滑度的先验。建模这种先验使其能够推广到不同程度的轨迹光滑度并非易事。例如,在使用多项式函数作为连续时间表示时,若多项式函数的阶数不够高,可能会因过度平滑而导致轨迹估计中的细节丧失。
据我们所知,目前还没有系统性地比较基于视觉的SLAM中连续时间和离散时间公式之间的差异。这样的系统性分析对于指导机器人从业者设计未来的SLAM解决方案至关重要。因此,我们进行了一项广泛的定量分析,以了解这两种轨迹表示的各自优缺点。我们专注于批处理SLAM,结合视觉、惯性和全局定位(即全球定位系统(GPS))测量,还调查了每种传感器模式的贡献。IMU和GPS分别提供局部高频和全局低频测量,这些测量与相机测量互补。相机、IMU和GPS测量被融合在一起,以获得局部精确且长期无漂移的轨迹估计。我们在硬件在环仿真和实际飞行及地面机器人轨迹数据上进行了实验。
我们的实验表明,当传感器时间同步时,离散时间和连续时间表示会产生相同的结果。然而,当时间同步存在偏移时,连续时间表现更好。这个结果的主要原因是,在离散时间中估计时间偏移所做的简化假设并不总是成立。这些发现适用于飞行机器人和地面机器人。
总结来说,本研究的主要贡献是:
- 对基于视觉的SLAM中离散时间和连续时间轨迹表示的深入对比研究。
- 在硬件在环仿真和实际飞行及地面机器人数据上的广泛实验评估。
- 包含解决离散时间和连续时间SLAM问题的最新算法的模块化、高效软件架构。我们发布了完整的开源代码。
II. 相关工作
在逼近连续函数的常见方法中,时域基函数是一种流行的选择。在时域基函数集合中,B样条 [5],[12] 具有对轨迹表示有用的性质:局部性和平滑性。B样条通过一组控制点定义连续时间演化。在任何时刻的采样仅依赖于控制点的局部子集(局部性)。该子集的大小对应于B样条的阶数 ( k ) (k) (k)。阶数为 ( k ) (k) (k)的B样条是一个 ( C k − 1 ) (C^{k-1}) (Ck−1) 类的函数(平滑性)。其他适合的基函数选择包括小波 [13]。高斯过程也被用于表示用于批量状态估计问题的连续时间轨迹 [14]。
近年来的研究尝试减少从B样条采样和计算导数的计算复杂度。在 [12] 中,提出了一种新的推导方法,用于计算累计B样条的时间导数。该方法将计算复杂度从与样条阶数的平方关系降低到线性关系。另一种针对累计B样条的高效非均匀分割插值方法也在 [15] 中提出。与我们工作最相关的连续时间轨迹表示应用包括多传感器标定 [5],[8]、3D重建 [6],[10]、事件相机的视觉惯性里程计 [7] 以及批量状态估计 [14]。
经典离散时间SLAM公式的文献非常广泛。由于篇幅限制,我们参考了文献 [1] 中的综述论文,以了解离散SLAM公式的概述。与连续时间不同,离散时间需要特定的算法来估计不同传感器之间的时间偏移。在我们的离散时间实现中,我们使用了 [3] 中提出的方法来估计相机-IMU的时间偏移。与 [16] 中的方法类似,我们也使用了相似的方法来估计GPS-IMU的时间偏移。在第III-B节中,我们将更详细地描述这两种方法。

图 2: (a) 批量轨迹估计过程的步骤。样条生成仅应用于连续时间估计。 (b) 估计过程中涉及的帧和位置。实线黑色表示可优化的、已校准的变换,虚线表示位置测量,虚点线表示时间变化的估计变换。点状线表示后者的轨迹。红色、绿色和蓝色箭头分别表示帧的 x、y 和 z 轴。
III. 方法论
我们使用多步骤的方法来解决估计问题,其中在进行全批量优化之前需要进行一些初始化步骤。图2(a)展示了连续时间和离散时间方法的优化流程图。参考框架如图2(b)所示。 W W W是固定的世界框架,其 z z z轴与重力对齐。当可用时,GPS测量会以该框架表示。 B B B是运动的机体框架,我们将其设置为IMU框架。 C C C是相机框架。 P P P是GPS天线的位置。需要注意的是,这并不是一个完整的6自由度框架,因为GPS测量没有提供方向信息。我们使用符号 ( ⋅ ) w (\cdot)^{w} (⋅)w表示世界框架 W W W中的量。类似的符号也适用于其他参考框架。相对于 W W W的 B B B在时间 t k t_{k} tk的位置信息、方向和速度分别表示为 p b k w ∈ R 3 , R b k w ∈ R 3 × 3 \mathbf{p}_{b_{k}}^{w} \in \mathbb{R}^{3}, \mathbf{R}_{b_{k}}^{w} \in \mathbb{R}^{3 \times 3} pbkw∈R3,Rbkw∈R3×3(属于3D旋转群 S O ( 3 ) S O(3) SO(3)),和 v b k w ∈ R 3 \mathbf{v}_{b_{k}}^{w} \in \mathbb{R}^{3} vbkw∈R3。我们使用 4 × 4 4 \times 4 4×4矩阵, T ∈ S E ( 3 ) \mathbf{T} \in S E(3) T∈SE(3)(特殊欧几里得群)来表示6自由度的欧几里得变换。
GPS测量包括GPS天线在世界框架中的位置, p p w ∈ R 3 \mathbf{p}_{p}^{w} \in \mathbb{R}^{3} ppw∈R3。第 i i i个3D视觉地标在世界框架中的位置是 p l i w ∈ R 3 \mathbf{p}_{l_{i}}^{w} \in \mathbb{R}^{3} pliw∈R3。集合 L \mathcal{L} L包含所有3D视觉地标。时间 t i c t_{i}^{c} tic是相机和IMU之间的时间偏移,因此 t i m u = t c a m + t i c t_{i m u}=t_{c a m}+t_{i}^{c} timu=tcam+tic。使用相同的惯例, t i g t_{i}^{g} tig是GPS-IMU时间偏移。包含优化变量的状态向量是 c X { }^{c} \mathcal{X} cX和 d X { }^{d} \mathcal{X} dX,分别对应于连续时间和离散时间方法。它们将在第III-A节和III-B节中介绍。变换 T i c \mathbf{T}_{i}^{c} Tic是相机和IMU之间的外参标定矩阵。向量 p p b ∈ R 3 \mathbf{p}_{p}^{b} \in \mathbb{R}^{3} ppb∈R3是GPS天线在机体框架中的位置。我们在连续时间中使用 c B { }^{c} \mathcal{B} cB来表示IMU偏置,在离散时间中使用 d B { }^{d} \mathcal{B} dB。它们分别在第III-A节和III-B节中介绍。
在本研究中,我们专注于全局快门相机,这种相机在基于视觉的SLAM系统中是常见的选择。初始相机姿态和3D地标是通过使用COLMAP [17] 获取的。COLMAP是一个单目结构从运动(Structure-from-Motion)管道,在计算机视觉和机器人社区中广泛使用。COLMAP重建的相机姿态和3D地标是在无尺度参考框架 G G G中表示的, G G G是一个固定框架,定义方式是使得第一个相机姿态等于单位矩阵。我们使用符号“ - ”表示传感器测量,使用符号 ∗ ^ \hat{*} ∗^表示真实值测量。
A. 连续时间表示
我们使用累积B样条曲线来表示连续时间轨迹。一个阶数为 k k k、具有 N + 1 N+1 N+1控制节点 x i \mathbf{x}_{i} xi的均匀B样条曲线定义为
x ( t ) = ∑ i = 0 N B i , k ( t ) x i \begin{equation*} \mathbf{x}(t)=\sum_{i=0}^{N} B_{i, k}(t) \mathbf{x}_{i} \tag{1} \end{equation*} x(t)=i=0∑NBi,k(t)xi(1)
其中 t t t是时间变量。控制点在时间上均匀分布,间隔为 Δ t \Delta t Δt,即 t i = t 0 + i Δ t t_{i}=t_{0}+i \Delta t ti=t0+iΔt, B i , k ( t ) B_{i, k}(t) Bi,k(t)由De Boor-Cox递推公式给出 [18]。对于累积B样条,式(1)可以重写为
x ( t ) = B ~ 0 , k ( t ) x 0 + ∑ i = 0 N B ~ i , k ( t ) d i \begin{equation*} \mathbf{x}(t)=\tilde{B}_{0, k}(t) \mathbf{x}_{0} + \sum_{i=0}^{N} \tilde{B}_{i, k}(t) \mathbf{d}_{i} \tag{2} \end{equation*} x(t)=B~0,k(t)x0+i=0∑NB~i,k(t)di(2)
其中 B ~ i , k ( t ) = ∑ s = i N B s , k ( t ) \tilde{B}_{i, k}(t) = \sum_{s=i}^{N} B_{s, k}(t) B~i,k(t)=∑s=iNBs,k(t), d i = x i − x i − 1 \mathbf{d}_{i} = \mathbf{x}_{i} - \mathbf{x}_{i-1} di=xi−xi−1。均匀B样条的系数是常数,可以写成矩阵形式 [19]。这种矩阵形式也可以用于累积B样条。结合矩阵公式 [19] 和在 [12] 中提出的均匀表示,计算可以简化,并且在时间 t t t从B样条中采样的公式变为
x ( u ) = x i + ∑ j = 1 k − 1 λ j ( u ) ⋅ d j i \begin{equation*} \mathbf{x}(u)=\mathbf{x}_{i} + \sum_{j=1}^{k-1} \lambda_{j}(u) \cdot \mathbf{d}_{j}^{i} \tag{3} \end{equation*} x(u)=xi+j=1∑k−1λj(u)⋅dji(3)
在 \cite{12} 中提出的统一时间表示定义了 u ( t ) u(t) u(t),其中 t ∈ [ t i , t i + 1 ) t \in [t_{i}, t_{i+1}) t∈[ti,ti+1),表示自该段开始以来经过的归一化时间。定义 h ( t ) = t − t 0 Δ t h(t) = \frac{t - t_{0}}{\Delta t} h(t)=Δtt−t0,那么 u ( t ) u(t) u(t) 可以计算为 u ( t ) = h ( t ) − i u(t) = h(t) - i u(t)=h(t)−i。系数 λ j ( u ) ∈ R \lambda_{j}(u) \in \mathbb{R} λj(u)∈R 是常数,并且仅依赖于 B 样条的阶数(参见 \cite{12} 中的方程 (18.21))。差分向量为 d j i = x i + j − x i + j − 1 \mathbf{d}_{j}^{i} = \mathbf{x}_{i+j} - \mathbf{x}_{i+j-1} dji=xi+j−xi+j−1。在 \cite{20} 中,针对 Lie 群元素推导了累积 B 样条的公式。在 Lie 群 S O ( 3 ) SO(3) SO(3) 中,加法对应于矩阵乘法,但不定义通过标量 λ \lambda λ 的缩放操作。缩放操作要求将群元素 R ∈ S O ( 3 ) \mathbf{R} \in SO(3) R∈SO(3) 映射到向量空间(Lie 代数),执行缩放操作,然后重新映射回 Lie 群: Exp ( λ ⋅ log ( R ) ) \operatorname{Exp}(\lambda \cdot \log(\mathbf{R})) Exp(λ⋅log(R))。Lie 代数中的元素可以通过指数映射 Exp ( ⋅ ) \operatorname{Exp}(\cdot) Exp(⋅) 映射到 Lie 群。逆操作是对数映射 log ( ⋅ ) \log(\cdot) log(⋅)。对于 S O ( 3 ) SO(3) SO(3) 的累积 B 样条公式为:
R ( u ) = R i ⋅ ∏ j = 1 k − 1 Exp ( λ j ( u ) ⋅ d j i ) (4) \mathbf{R}(u) = \mathbf{R}_{i} \cdot \prod_{j=1}^{k-1} \operatorname{Exp}\left( \lambda_{j}(u) \cdot \mathbf{d}_{j}^{i} \right) \tag{4} R(u)=Ri⋅j=1∏k−1Exp(λj(u)⋅dji)(4)
- 初始化: 我们的连续时间轨迹估计流程的第一步是拟合一个 B 样条到通过 COLMAP 估计的 K K K 个相机位姿: p c k g , R c k g \mathbf{p}_{c_{k}}^{g}, \mathbf{R}_{c_{k}}^{g} pckg,Rckg。 N N N 个控制节点的初始值 p c i g \mathbf{p}_{c_{i}}^{g} pcig 和 R c i g \mathbf{R}_{c_{i}}^{g} Rcig 是通过对 COLMAP 相机位姿在时刻 t i = t 0 + i Δ t t_{i}=t_{0}+i \Delta t ti=t0+iΔt 进行线性插值获得的,其中 t 0 t_{0} t0 是第一个相机位姿的时间, Δ t \Delta t Δt 是控制节点频率的倒数。然后,控制节点被优化,以最小化目标函数
min p c i g , R c i g ∑ j = 1 M ∥ p c g ( u ( t j ) ) − p c j g ∥ 2 + ∥ log ( R c g ( u ( t j ) ) t ⋅ R c j g ) ∥ 2 (5) \min _{\mathbf{p}_{c_{i}}^{g}, \mathbf{R}_{c_{i}}^{g}} \sum_{j=1}^{M}\left\|\mathbf{p}_{c}^{g}\left(u\left(t_{j}\right)\right)-\mathbf{p}_{c_{j}}^{g}\right\|^{2} + \left\|\log \left(\mathbf{R}_{c}^{g}\left(u\left(t_{j}\right)\right)^{t} \cdot \mathbf{R}_{c_{j}}^{g}\right)\right\|^{2} \tag{5} pcig,Rcigminj=1∑M pcg(u(tj))−pcjg 2+ log(Rcg(u(tj))t⋅Rcjg) 2(5)
其中 M M M 是误差的数量。测量值 p c j g \mathbf{p}_{c_{j}}^{g} pcjg 是通过对相机位姿 p c k g \mathbf{p}_{c_{k}}^{g} pckg 和 p c k + 1 g \mathbf{p}_{c_{k+1}}^{g} pck+1g 进行线性插值得到的, t j ∈ [ t k , t k + 1 ) t_{j} \in \left[t_{k}, t_{k+1}\right) tj∈[tk,tk+1)。我们同样对旋转矩阵 R c j g \mathbf{R}_{c_{j}}^{g} Rcjg 使用球面线性插值(SLERP)。我们最小化目标函数直至收敛,通常在 20 次迭代以内。此步骤的结果是连续时间轨迹 c T c g = { p c i g , R c i g } {}^{c} \mathcal{T}_{c}^{g} = \left\{\mathbf{p}_{c_{i}}^{g}, \mathbf{R}_{c_{i}}^{g}\right\} cTcg={pcig,Rcig},它表示参考坐标系 G G G 中的相机位姿。我们将相机位姿转换为车体位姿,并得到轨迹 c T b g = { p b i g , R b i g } {}^{c} \mathcal{T}_{b}^{g} = \left\{\mathbf{p}_{b_{i}}^{g}, \mathbf{R}_{b_{i}}^{g}\right\} cTbg={pbig,Rbig}。 T i c \mathbf{T}_{i}^{c} Tic 的初值通过使用标定工具箱 Kalibr (8) 获得。
- 估计尺度与对齐: 我们的连续时间轨迹估计流程的第二步是估计轨迹 c T b g {}^{c} \mathcal{T}_{b}^{g} cTbg 的实际尺度,并找到一个变换将其对齐到重力对齐坐标系。当 GPS 测量可用时,我们使用 [22] 中提出的方法获取初步估计的 6 自由度变换 T g w \mathbf{T}_{g}^{w} Tgw 和尺度 s s s。该方法找到最小二乘解,最小化相对于 T g w \mathbf{T}_{g}^{w} Tgw 和 s s s,从样条中采样得到的 p b g ( u ( t j ) ) \mathbf{p}_{b}^{g}(u(t_{j})) pbg(u(tj)) 与 GPS 测量 p ‾ p j w \overline{\mathbf{p}}_{p_{j}}^{w} ppjw 之间的差异。此处假设 GPS 天线与 IMU 之间的位置偏移 p p b \mathbf{p}_{p}^{b} ppb 为零。然后,通过最小化目标函数
min T g w , s , p p b , t i g ∑ j = 1 D ∥ p ‾ p j w − p p j w ∥ 2 (6) \min _{\mathbf{T}_{g}^{w}, s, \mathbf{p}_{p}^{b}, t_{i}^{g}} \sum_{j=1}^{D}\left\|\overline{\mathbf{p}}_{p_{j}}^{w} - \mathbf{p}_{p_{j}}^{w}\right\|^{2} \tag{6} Tgw,s,ppb,tigminj=1∑D ppjw−ppjw 2(6)
其中,第 j j j 个 GPS 测量 p ‾ p j w \overline{\mathbf{p}}_{p_{j}}^{w} ppjw 在时刻 t j t_{j} tj 可用。预测的天线位置通过从样条中采样得到: p p j w = s R b j w p p b + p b j w , R b j w = R g w R b g ( u ( t j + t i g ) ) \mathbf{p}_{p_{j}}^{w} = s \mathbf{R}_{b_{j}}^{w} \mathbf{p}_{p}^{b} + \mathbf{p}_{b_{j}}^{w}, \mathbf{R}_{b_{j}}^{w} = \mathbf{R}_{g}^{w} \mathbf{R}_{b}^{g}\left(u(t_{j} + t_{i}^{g})\right) ppjw=sRbjwppb+pbjw,Rbjw=RgwRbg(u(tj+tig)),且 p b j w = s R g w p b g ( u ( t j + t i g ) ) + p g w \mathbf{p}_{b_{j}}^{w} = s \mathbf{R}_{g}^{w} \mathbf{p}_{b}^{g}\left(u(t_{j} + t_{i}^{g})\right) + \mathbf{p}_{g}^{w} pbjw=sRgwpbg(u(tj+tig))+pgw。
当我们没有使用 GPS 测量时,我们利用 IMU 测量值来获得尺度的初步估计。我们在短时间内(通常为几秒钟)积分 IMU 测量值,得到一个小的轨迹段。该轨迹表示在重力对齐坐标系 I I I 中, I I I 是通过在 IMU 静止时收集的加速度计测量值估计得到的。如前所述,我们使用 [22] 方法获取变换 s , T g i s, \mathbf{T}_{g}^{i} s,Tgi。该变换应用于将 c T b g {}^{c} \mathcal{T}_{b}^{g} cTbg 转换到坐标系 I I I。
- 全批优化:我们使用在初始化步骤中估计的 T g w \mathbf{T}_{g}^{w} Tgw和 s s s,将轨迹 c T b g {}^{c} \mathcal{T}_{b}^{g} cTbg转换到全局坐标系 W W W(如果没有使用GPS,则转换到 I I I): c T b w = { p b i w , R b i w } . {}^{c} \mathcal{T}_{b}^{w} = \left\{ \mathbf{p}_{b_{i}}^{w}, \mathbf{R}_{b_{i}}^{w} \right\}. cTbw={pbiw,Rbiw}.同样,3D地标 p l r g \mathbf{p}_{l_{r}}^{g} plrg也被转换到 W W W: p l r w = s R g w p l r g + p g w \mathbf{p}_{l_{r}}^{w} = s \mathbf{R}_{g}^{w} \mathbf{p}_{l_{r}}^{g} + \mathbf{p}_{g}^{w} plrw=sRgwplrg+pgw在全批优化中,状态向量 c X {}^{c} \mathcal{X} cX通过最小化以下代价函数来估计:
min c X ∑ k = 1 K ∑ r ∈ R k ∥ e k , r v ∥ W v 2 + ∑ m = 1 M ( ∥ e m a ∥ W a 2 + ∥ e m ω ∥ W w 2 ) + ∑ d = 1 D ∥ e d g p s ∥ W g p s 2 + ∑ f = 1 F ( ∥ e f b a ∥ W b a 2 + ∥ e f b ω ∥ W b ω 2 ) (7) \begin{aligned} & \min_{{}^c \mathcal{X}} \sum_{k=1}^{K} \sum_{r \in \mathcal{R}_k} \left\| \mathbf{e}_{k, r}^{\mathrm{v}} \right\|_{\mathbf{W}_{\mathrm{v}}}^{2} + \sum_{m=1}^{M} \left( \left\| \mathbf{e}_{m}^{\mathrm{a}} \right\|_{\mathbf{W}_{\mathrm{a}}}^{2} + \left\| \mathbf{e}_{m}^{\omega} \right\|_{\mathbf{W}_{\mathrm{w}}}^{2} \right) \\ & + \sum_{d=1}^{D} \left\| \mathbf{e}_{d}^{\mathrm{gps}} \right\|_{\mathbf{W}_{\mathrm{gps}}}^{2} + \sum_{f=1}^{F} \left( \left\| \mathbf{e}_{f}^{\mathrm{b}_{\mathrm{a}}} \right\|_{\mathbf{W}_{\mathrm{b}_{\mathrm{a}}}}^{2} + \left\| \mathbf{e}_{f}^{\mathrm{b}_{\omega}} \right\|_{\mathbf{W}_{\mathrm{b}_{\omega}}}^{2} \right) \end{aligned}\tag{7} cXmink=1∑Kr∈Rk∑ ek,rv Wv2+m=1∑M(∥ema∥Wa2+∥emω∥Ww2)+d=1∑D∥edgps∥Wgps2+f=1∑F( efba Wba2+ efbω Wbω2)(7)
优化这个代价函数可以得到最大后验(MAP)估计的状态向量 c X {}^{c} \mathcal{X} cX,该结果是通过使用概率连续SLAM公式和高斯分布对所有测量进行推导得到的。
B. 离散时间表示
在离散时间公式中,轨迹通过相机的频率表示为物体位姿: d T b w = { p b k w , R b k w } { }^{d} \mathcal{T}_{b}^{w}=\left\{\mathbf{p}_{b_{k}}^{w}, \mathbf{R}_{b_{k}}^{w}\right\} dTbw={pbkw,Rbkw}。相机和IMU之间的时间偏移使用[3]中提出的方法进行估计,该方法已集成在VINSMono[23]中,这是一个最先进的视觉惯性里程计管道。该方法建议通过平移2D图像特征来考虑相机和IMU测量之间的时间偏移。它假设相机运动在短时间内(例如,在连续帧之间)具有恒定速度,并基于这一假设计算图像平面上2D特征的速度。然后,使用这个速度来平移特征位置,以适应与相机和IMU之间时间延迟相对应的短时间(参见[3]中的方程(4))。这样可以将时间偏移包含在估计过程中。为了定义GPS误差,轨迹在GPS测量的时间点进行插值。IMU-GPS时间偏移在插值因子中进行处理,类似于[16]中的方法。
- 初始化:与Sec. III-A1类似,我们计算从COLMAP估计的相机位姿得到的物体位姿,然后使用应用[22]得到的6自由度和尺度变换将其转换到世界坐标系 W W W。
- 全批优化:使用与Sec. III-A2中类似的概率SLAM公式,我们推导出要最小化的代价函数:
min d X ∑ k = 1 K ∑ r ∈ R k ∥ e k , r v ∥ W v 2 + ∑ k = 1 K ∥ e k i ∥ W i 2 + ∑ k = 1 K ( ∥ e k b a ∥ W b a 2 + ∥ e k b ω ∥ W b ω 2 ) + ∑ d = 1 D ∥ e d g p s ∥ W g p s 2 \begin{align*} & \min _{d \mathcal{X}} \sum_{k=1}^{K} \sum_{r \in \mathcal{R}_{k}}\left\|\mathbf{e}_{k, r}^{\mathrm{v}}\right\|_{\mathbf{W}_{\mathrm{v}}}^{2}+\sum_{k=1}^{K}\left\|\mathbf{e}_{k}^{\mathrm{i}}\right\|_{\mathbf{W}_{\mathbf{i}}}^{2}+\sum_{k=1}^{K}\left(\left\|\mathbf{e}_{k}^{\mathrm{b}_{\mathrm{a}}}\right\|_{\mathbf{W}_{\mathrm{b}_{\mathrm{a}}}}^{2}+\right. \\ &\left.\left\|\mathbf{e}_{k}^{\mathrm{b}_{\omega}}\right\|_{\mathbf{W}_{\mathrm{b}_{\omega}}}^{2}\right)+\sum_{d=1}^{D}\left\|\mathbf{e}_{d}^{\mathrm{gps}}\right\|_{\mathbf{W}_{\mathrm{gps}}}^{2} \tag{8} \end{align*} dXmink=1∑Kr∈Rk∑ ek,rv Wv2+k=1∑K eki Wi2+k=1∑K( ekba Wba2+ ekbω Wbω2)+d=1∑D∥edgps∥Wgps2(8)
状态向量为 d X = { d T b w , V b w , L , t i c , T i c , t i g , p p b , d B } { }^{d} \mathcal{X}=\left\{{ }^{d} \mathcal{T}_{b}^{w}, \mathcal{V}_{b}^{w}, \mathcal{L}, t_{i}^{c}, \mathbf{T}_{i}^{c}, t_{i}^{g}, \mathbf{p}_{p}^{b},{ }^{d} \mathcal{B}\right\} dX={dTbw,Vbw,L,tic,Tic,tig,ppb,dB}。集合 V b w \mathcal{V}_{b}^{w} Vbw包含速度向量: v b k w \mathbf{v}_{b_{k}}^{w} vbkw。集合 d B { }^{d} \mathcal{B} dB包含加速度计和陀螺仪偏差向量: b a k \mathbf{b}_{\mathrm{a}_{k}} bak和 b ω k \mathbf{b}_{\omega_{k}} bωk。世界坐标系 W W W中的初始3D地标位置类似于在III-A2中描述的方法获得。重投影误差 e k , r v \mathbf{e}_{k, r}^{\mathrm{v}} ek,rv和GPS误差 e d g p s \mathbf{e}_{d}^{\mathrm{gps}} edgps的定义与SecIII-A2相同,唯一的区别是轨迹位姿是以离散时间表示的。误差 e k i \mathbf{e}_{k}^{\mathrm{i}} eki是惯性残差。我们使用[4]中提出的IMU预积分公式计算这些残差。每个惯性误差 e k i \mathbf{e}_{k}^{\mathrm{i}} eki根据在 [ t k − 1 , t k ] \left[t_{k-1}, t_{k}\right] [tk−1,tk]区间内的预积分IMU测量,约束了连续的 k − 1 k-1 k−1和 k k k位姿与速度(参见[4]中的方程(45))。误差 e k b a \mathbf{e}_{k}^{\mathrm{b}_{\mathrm{a}}} ekba和 e k b ω \mathbf{e}_{k}^{\mathbf{b}_{\omega}} ekbω约束了偏差随机游走(参见[4]中的方程(48))。
IV. 实验
我们比较了连续时间和离散时间表示在估计轨迹和时间偏移上的准确性。用于此比较的评估指标如下:
-
位置绝对轨迹误差 ( A T E P \mathrm{ATE}_{\mathrm{P}} ATEP) [m]:
A T E P = 1 N ∑ k = 0 N − 1 ∥ p b k w − p ^ b k w ∥ 2 \mathrm{ATE}_{\mathrm{P}} = \sqrt{\frac{1}{N} \sum_{k=0}^{N-1} \left\|\mathbf{p}_{b_{k}}^{w} - \hat{\mathbf{p}}_{b_{k}}^{w}\right\|^{2}} ATEP=N1k=0∑N−1 pbkw−p^bkw 2 -
旋转绝对轨迹误差 ( A T E R \mathrm{ATE}_{\mathrm{R}} ATER) [deg]:
A T E R = 1 N ∑ k = 0 N − 1 ∥ log ( ( R b k w ) t ⋅ R ^ b k w ) ∥ 2 \mathrm{ATE}_{\mathrm{R}} = \sqrt{\frac{1}{N} \sum_{k=0}^{N-1} \left\| \log \left( \left( \mathbf{R}_{b_{k}}^{w} \right)^{t} \cdot \hat{\mathbf{R}}_{b_{k}}^{w} \right) \right\|^{2}} ATER=N1k=0∑N−1 log((Rbkw)t⋅R^bkw) 2
在连续时间的情况下,轨迹是在相机测量的时间戳处进行采样,以获得 p b k w \mathbf{p}_{b_{k}}^{w} pbkw 和 R b k w \mathbf{R}_{b_{k}}^{w} Rbkw。我们在硬件在环仿真和两个真实世界数据集上进行了多次实验。硬件在环仿真使得能够深入评估这两种轨迹表示在估计时间偏移方面的能力,因为已知真实值。我们研究了机器人类型(飞行机器人或地面机器人)是否对轨迹表示产生影响,使用这两个真实世界数据集进行分析。我们使用 Ceres Solver [25] 并选择 Levenberg-Marquardt 算法进行优化。导数通过求解器中包含的自动微分方法计算。
表 I: B-样条阶数的消融研究。ATE P _{P} P 单位为米,ATE R _{\mathrm{R}} R 单位为度,时间偏移 t i c t_{i}^{c} tic 单位为毫秒。每个序列的最佳值以粗体表示。
| Order | Ev. | EuRoC sequence | |||||
|---|---|---|---|---|---|---|---|
| metric | V101 | V102 | V103 | V201 | V202 | V203 | |
| 4 | A T E P [ m ] \mathrm{ATE}_{\mathrm{P}}[\mathrm{m}] ATEP[m] | 0.024 \mathbf{0 . 0 2 4} 0.024 | 0.014 \mathbf{0 . 0 1 4} 0.014 | 0.011 \mathbf{0 . 0 1 1} 0.011 | 0.011 \mathbf{0 . 0 1 1} 0.011 | 0.011 | 0.024 |
| A T E R [ d e g ] \mathrm{ATE}_{\mathrm{R}}[\mathrm{deg}] ATER[deg] | 5.5 \mathbf{5 . 5} 5.5 | 2.1 \mathbf{2 . 1} 2.1 | 2.3 \mathbf{2 . 3} 2.3 | 0.6 \mathbf{0 . 6} 0.6 | 0.8 | 1.0 | |
| t i c [ m s ] t_{i}^{c}[\mathrm{~ms}] tic[ ms] | 0.9 | 3.2 | − 1.4 \mathbf{- 1 . 4} −1.4 | 10.8 | 1.0 | 2.2 | |
| 5 | A T E P [ m ] \mathrm{ATE}_{\mathrm{P}}[\mathrm{m}] ATEP[m] | 0.024 \mathbf{0 . 0 2 4} 0.024 | 0.014 \mathbf{0 . 0 1 4} 0.014 | 0.011 \mathbf{0 . 0 1 1} 0.011 | 0.011 \mathbf{0 . 0 1 1} 0.011 | 0.010 \mathbf{0 . 0 1 0} 0.010 | 0.019 |
| A T E R [ d e g ] \mathrm{ATE}_{\mathrm{R}}[\mathrm{deg}] ATER[deg] | 5.5 \mathbf{5 . 5} 5.5 | 2.2 | 2.3 \mathbf{2 . 3} 2.3 | 0.9 | 0.7 \mathbf{0 . 7} 0.7 | 0.8 | |
| t i c [ m s ] t_{i}^{c}[\mathrm{~ms}] tic[ ms] | 0.3 | -5.8 | 2.0 | -1.8 | 0.0 \mathbf{0 . 0} 0.0 | 0.5 | |
| 6 | A T E P [ m ] \mathrm{ATE}_{\mathrm{P}}[\mathrm{m}] ATEP[m] | 0.024 \mathbf{0 . 0 2 4} 0.024 | 0.014 \mathbf{0 . 0 1 4} 0.014 | 0.011 \mathbf{0 . 0 1 1} 0.011 | 0.012 | 0.010 \mathbf{0 . 0 1 0} 0.010 | 0.010 \mathbf{0 . 0 1 0} 0.010 |
| A T E R [ d e g ] \mathrm{ATE}_{\mathrm{R}}[\mathrm{deg}] ATER[deg] | 5.5 \mathbf{5 . 5} 5.5 | 2.1 \mathbf{2 . 1} 2.1 | 2.3 \mathbf{2 . 3} 2.3 | 0.8 | 0.7 \mathbf{0 . 7} 0.7 | 0.6 \mathbf{0 . 6} 0.6 | |
| t i c [ m s ] t_{i}^{c}[\mathrm{~ms}] tic[ ms] | 0.2 \mathbf{0 . 2} 0.2 | 1.3 \mathbf{1 . 3} 1.3 | − 1.4 \mathbf{- 1 . 4} −1.4 | 1.2 \mathbf{1 . 2} 1.2 | 0.0 \mathbf{0 . 0} 0.0 | 0.2 \mathbf{0 . 2} 0.2 |
表 II: B-样条控制节点频率的消融研究。ATE P _{P} P 单位为米,ATE R _{R} R 单位为度,估计的时间偏移 t i c t_{i}^{c} tic 单位为毫秒。每个序列的最佳值以粗体表示。
| Node freq. | Ev. metric | EuRoC sequence | |||||
|---|---|---|---|---|---|---|---|
| V 101 \mathbf{V 1 0 1} V101 | V 102 \mathbf{V 1 0 2} V102 | V 103 \mathbf{V 1 0 3} V103 | V201 | V202 | V203 | ||
| 1 Hz | A T E P [ m ] \mathrm{ATE}_{\mathrm{P}}[\mathrm{m}] ATEP[m] | 0.028 | 0.120 | 0.077 | 0.020 | 0.187 | 0.075 |
| A T E R [ d e g ] \mathrm{ATE}_{\mathrm{R}}[\mathrm{deg}] ATER[deg] | 5.9 | 4.6 | 7.6 | 2.0 | 10.7 | 5.18 | |
| t i c [ m s ] t_{i}^{c}[\mathrm{~ms}] tic[ ms] | 6.6 | 19.3 | 1.2 | 0.0 | -45.6 | -19.0 | |
| 5 Hz | A T E P [ m ] \mathrm{ATE}_{\mathrm{P}}[\mathrm{m}] ATEP[m] | 0.023 \mathbf{0 . 0 2 3} 0.023 | 0.014 \mathbf{0 . 0 1 4} 0.014 | 0.011 \mathbf{0 . 0 1 1} 0.011 | 0.010 \mathbf{0 . 0 1 0} 0.010 | 0.010 \mathbf{0 . 0 1 0} 0.010 | 0.019 |
| A T E R [ d e g ] \mathrm{ATE}_{\mathrm{R}}[\mathrm{deg}] ATER[deg] | 5.6 | 2.1 \mathbf{2 . 1} 2.1 | 2.3 | 0.9 | 0.8 | 0.8 | |
| t i c [ m s ] t_{i}^{c}[\mathrm{~ms}] tic[ ms] | -1.9 | -2.8 | 1.7 | 4.0 | 2.6 | -1.5 | |
| 10 Hz | A T E P [ m ] \mathrm{ATE}_{\mathrm{P}}[\mathrm{m}] ATEP[m] | 0.024 | 0.014 \mathbf{0 . 0 1 4} 0.014 | 0.011 \mathbf{0 . 0 1 1} 0.011 | 0.012 | 0.010 \mathbf{0 . 0 1 0} 0.010 | 0.010 \mathbf{0 . 0 1 0} 0.010 |
| A T E R [ d e g ] \mathrm{ATE}_{\mathrm{R}}[\mathrm{deg}] ATER[deg] | 5.5 \mathbf{5 . 5} 5.5 | 2.1 \mathbf{2 . 1} 2.1 | 2.3 | 0.8 \mathbf{0 . 8} 0.8 | 0.7 \mathbf{0 . 7} 0.7 | 0.6 \mathbf{0 . 6} 0.6 | |
| t i c [ m s ] t_{i}^{c}[\mathrm{~ms}] tic[ ms] | 0.2 | 1.3 | -1.4 | 1.2 | 0.0 \mathbf{0 . 0} 0.0 | 0.2 \mathbf{0 . 2} 0.2 | |
| 20 Hz | A T E P [ m ] \mathrm{ATE}_{\mathrm{P}}[\mathrm{m}] ATEP[m] | 0.025 | 0.014 \mathbf{0 . 0 1 4} 0.014 | 0.011 \mathbf{0 . 0 1 1} 0.011 | 0.010 \mathbf{0 . 0 1 0} 0.010 | 0.010 \mathbf{0 . 0 1 0} 0.010 | 0.010 \mathbf{0 . 0 1 0} 0.010 |
| A T E R [ d e g ] \mathrm{ATE}_{\mathrm{R}}[\mathrm{deg}] ATER[deg] | 5.5 \mathbf{5 . 5} 5.5 | 2.1 \mathbf{2 . 1} 2.1 | 2.2 \mathbf{2 . 2} 2.2 | 1.2 | 0.7 \mathbf{0 . 7} 0.7 | 0.6 \mathbf{0 . 6} 0.6 | |
| t i c [ m s ] t_{i}^{c}[\mathrm{~ms}] tic[ ms] | -2.4 | 0.7 \mathbf{0 . 7} 0.7 | − 0.9 \mathbf{- 0 . 9} −0.9 | − 0.7 -\mathbf{0 . 7} −0.7 | -1.1 | 2.0 | |
| 100 Hz | A T E P [ m ] \mathrm{ATE}_{\mathrm{P}}[\mathrm{m}] ATEP[m] | 0.024 | 0.226 | 0.117 | 0.060 | 0.168 | 0.136 |
| A T E R [ d e g ] \mathrm{ATE}_{\mathrm{R}}[\mathrm{deg}] ATER[deg] | 8.8 | 8.4 | 12.1 | 6.6 | 11.1 | 5.6 | |
| t i c [ m s ] t_{i}^{c}[\mathrm{~ms}] tic[ ms] | 0.0 \mathbf{0 . 0} 0.0 | -4.1 | -3.0 | 0.0 | -1.3 | -0.5 |
我们在Ubuntu 18.04工作站上进行所有实验,配备Intel Core i7 3.2 GHz处理器,并使用8个核心进行优化。在所有实验中,优化问题在收敛之前一直进行求解,通常在50次迭代以内即可完成。
A. 硬件在环仿真:EuRoC数据集
EuRoC数据集[26]包含了在搭载立体相机和IMU的六旋翼飞行机器人上的序列。该数据集因其准确的地面真值和硬件同步的传感器而广为人知。假设相机与IMU之间的时间偏移为零。我们仅使用标有 V − \mathrm{V}_{-} V−的序列,这些序列包含来自运动捕捉系统的6自由度地面真值。序列根据难度(见[26]中的表2)分为易、中、难三类,反映了由光照条件、场景纹理和车辆运动引起的难度级别。困难序列包含具有挑战性的光照条件(例如,运动模糊)和快速运动,平均线性速度和角速度分别达到 0.9 m s − 1 0.9 \mathrm{~ms}^{-1} 0.9 ms−1和 0.75 r a d s − 1 0.75 \mathrm{rad} \mathrm{s}^{-1} 0.75rads−1。我们通过下采样和将零均值高斯噪声加入地面真值位置来模拟GPS测量。模拟GPS测量的频率为10 Hz,高斯噪声的标准偏差为0.1米。位置偏移 p p b \mathbf{p}_{p}^{b} ppb等于 0 ∈ R 3 \mathbf{0} \in \mathbb{R}^{3} 0∈R3。我们仅使用右相机的图像。
表 III: 在EuRoC数据集上,连续时间与离散时间方法的比较。ATE P _{P} P 单位为米,ATE R _{R} R 单位为度, t ^ i c \hat{t}_{i}^{c} t^ic(地面真值)和 t i c t_{i}^{c} tic(估计值)时间偏移单位为毫秒。每个序列中ATE P _{\mathrm{P}} P和ATE R _{\mathrm{R}} R的最佳值用粗体表示。
| Seq. | Continuous-time | Discrete-time | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| t ~ i c = 0 \tilde{t}_{i}^{c}=0 t~ic=0 [ms] | t ~ i c = 10 \tilde{t}_{i}^{c}=10 t~ic=10 [ms] | t ^ i c = 20 [ m s ] \hat{t}_{i}^{c}=20[\mathrm{~ms}] t^ic=20[ ms] | t ^ i c = 0 \hat{t}_{i}^{c}=0 t^ic=0 [ms] | t ^ i c = 10 \hat{t}_{i}^{c}=10 t^ic=10 [ms] | t ^ i c = 20 \hat{t}_{i}^{c}=20 t^ic=20 [ms] | |||||||
| A T E P / A T E R \mathrm{ATE}_{\mathrm{P}} / \mathrm{ATE}_{\mathrm{R}} ATEP/ATER | t i c t_{i}^{c} tic | A T E P / A T E R \mathrm{ATE}_{\mathrm{P}} / \mathrm{ATE}_{\mathrm{R}} ATEP/ATER | t i c t_{i}^{c} tic | ATE P _{\text {P }} P / ATE P { }_{\text {P }} P | t i c t_{i}^{c} tic | ATE P _{\text {P }} P / ATE P { }_{\text {P }} P | t i c t_{i}^{c} tic | ATE P _{\text {P }} P / ATE R { }_{\text {R }} R | t i c t_{i}^{c} tic | ATE / ^{\text {/ }} / / ATE P { }_{\text {P }} P | t i c t_{i}^{c} tic | |
| V101 | 0.024 / 5.5 | 0.2 | 0.024 / 5.5 | 11.0 | 0.024 / 5.5 | 22.2 | 0.016 / 5.6 | 0.3 | 0.016 / 5.6 | 9.1 | 0.016 / 5.6 | 18.6 |
| V102 | 0.014 / 2.1 | 1.3 | 0.014 / 2.1 | 9.7 | 0.014 / 2.1 | 20.6 | 0.024 / 2.4 | 0.0 | 0.026 / 2.3 | 4.6 | 0.031 / 2.2 | 9.3 |
| V103 | 0.011 / 2.3 0.011 / 2.3 0.011/2.3 | -1.4 | 0.011 / 2.3 | 11.8 | 0.011 / 2.3 | 22.3 | 0.018 / 2.7 | 0.0 | 0.020 / 2.6 | 3.5 | 0.024 / 2.6 | 7.2 |
| V201 | 0.012 / 0.8 | 1.2 | 0.010 / 0.9 | 9.7 | 0.010 / 0.9 | 19.0 | 0.009 / 1.0 | 0.3 | 0.010 / 1.0 | 8.1 | 0.012 / 1.0 | 16.4 |
| V202 | 0.010 / 0.7 | 0.0 | 0.010 / 0.7 | 10.0 | 0.010 / 0.7 | 20.0 | 0.019 / 0.8 | 0.0 | 0.021 / 0.9 | 8.5 | 0.024 / 1.1 | 16.7 |
| V203 | 0.010 / 0.6 | 0.2 | 0.010 / 0.6 | 10.6 | 0.010 / 0.6 | 21.5 | 0.033 / 1.1 | 0.0 | 0.036 / 1.2 | 4.0 | 0.040 / 1.3 | 7.5 |
表 IV: 全批次优化时间。对于连续时间表示,我们使用了阶数为6的B样条和控制频率 ∈ [ 1 , 2 , 10 , 20 , 100 ] [ H z ] \in[1,2,10,20,100][\mathrm{Hz}] ∈[1,2,10,20,100][Hz]。时间值单位为分钟,轨迹长度单位为米。每个序列的最低优化时间用粗体表示。
| Seq. | Length [ m ] [\mathbf{m}] [m] | C T \mathbf{C T} CT | 1 H z \mathbf{1} \mathbf{~ H z} 1 Hz | 2 H z \mathbf{2} \mathbf{~ H z} 2 Hz | 10 H z \mathbf{1 0} \mathbf{~ H z} 10 Hz | ||
|---|---|---|---|---|---|---|---|
| 20 H z \mathbf{2 0} \mathbf{~ H z} 20 Hz | 100 H z \mathbf{1 0 0} \mathbf{~ H z} 100 Hz | DT | |||||
| V101 | 52.6 | 13 | 21 | 36 | 37 | 12 \mathbf{1 2} 12 | |
| V102 | 75.9 | 19 \mathbf{1 9} 19 | 20 | 25 | 49 | 57 | 28 |
| V103 | 79.0 | 24 | 37 | 22 | 46 | 46 | 21 \mathbf{2 1} 21 |
| V201 | 36.5 | 6 | 5 \mathbf{5} 5 | 13 | 10 | 13 | 15 |
| V202 | 83.2 | 44 | 54 | 73 | 44 | 77 | 21 \mathbf{2 1} 21 |
| V203 | 86.1 | 18 | 16 | 39 | 50 | 31 | 14 \mathbf{1 4} 14 |
- B样条的消融研究: 我们进行了一项研究,以评估B样条控制点的阶数和频率对轨迹和相机-IMU时间偏差估计的影响。时间偏差的初始值设置为0毫秒。B样条阶数的消融研究结果见表I。需要使用阶数为6的B样条,该阶数对应于编码加速度的三次多项式,以正确估计相机-IMU时间偏差。这个结论与[8]中的发现一致。阶数大于6对估计结果没有任何影响。当B样条阶数为6时,时间偏差的值接近但不完全为0毫秒。由于我们将优化问题求解至收敛,因此该解已达到代价函数的局部最小值。局部最小值离全局最小值的距离未知,通常情况下,MAP估计的全局最优解可能与地面真实值不同,原因在于建模误差。
我们将B样条的阶数设置为6,并对控制节点频率进行消融研究。结果见表II。ATE和 t i c t_{i}^{c} tic的值表明,10 Hz的频率是最佳选择。提高到20 Hz没有显著优势,反而使优化计算开销增大。当频率过高时,例如100 Hz,难以实现良好的收敛。我们得出结论,阶数为6且控制节点频率为 10 / 20 H z 10 / 20 \mathrm{~Hz} 10/20 Hz是表示该数据集轨迹的适当参数。
- 轨迹表示的评估: 在这组实验中,我们评估了连续时间和离散时间轨迹表示在 A T E P , A T E R \mathrm{ATE}_{\mathrm{P}}, \mathrm{ATE}_{\mathrm{R}} ATEP,ATER、估计相机-IMU时间偏差的准确性和计算成本方面的表现。根据IV-A1节的研究结果,我们使用阶数为6且控制节点频率为10 Hz的B样条。为了评估相机-IMU时间偏差的估计准确性,我们模拟了相机数据流中的延迟,类似于[3]。我们进行的实验包括0、10和20毫秒的延迟。该比较结果见表III。这些结果表明,当相机和IMU是时间同步时,两种轨迹表示的准确度相似(见 t i c = 0 t_{i}^{c}=0 tic=0对应的列)。然而,使用连续时间在序列V102、V103、V202和V203中,机器人运动较快的中等和困难序列中,提供了较低的 A T E P \mathrm{ATE}_{\mathrm{P}} ATEP。
当相机和IMU没有时间同步时,连续时间是最佳的轨迹表示。该表示能够正确估计时间偏差,并产生类似于时间同步传感器的ATE。在快速轨迹的情况下,离散时间表示在估计相机-IMU时间偏差时存在问题。可以从序列V102、V103、V202和V203中估计的时间偏差与真实值之间的巨大差异看出这一点。造成这种结果的原因是,在计算2D特征的速度时,假设相机在连续相机帧之间的运动是匀速的,如III-B节中所述。对于快速运动,这一假设不再准确。表IV包含了优化时间,即求解器收敛所花费的时间。
- 不同传感器模态贡献的消融研究: 在这一部分,我们感兴趣的是研究每个传感器模态(即视觉、惯性和GPS)对轨迹估计准确性的贡献。为此,我们分别求解了连续时间和离散时间情况下的优化问题(见方程(7)和(8)),并进行了所有可能的至少两种传感器组合。对于连续时间表示,我们使用了阶数为6、控制节点频率为10 Hz的B样条。此次分析的 A T E P \mathrm{ATE}_{\mathrm{P}} ATEP和 A T E R \mathrm{ATE}_{\mathrm{R}} ATER值见表V和表VI。结果表明,视觉是最重要的传感器模态。对于两种轨迹表示,视觉- GPS配置在大多数序列中产生了最低的ATE P _{\mathrm{P}} P。在这种情况下,COLMAP重建的轨迹通过使用噪声模拟的GPS测量值转变为重力对准框架,然后与这些测量值一起重新优化。COLMAP能够在该数据集的每个序列中重建出准确的轨迹。因此,将惯性测量包含在估计过程中并没有带来显著的好处。
表V: 不同传感器模态贡献的消融研究。误差度量是ATE P _{P} P(单位:米)。V: 视觉,I: 惯性,G: 模拟GPS。每个序列的最佳值用粗体表示。
| Sensors | Traj. | EuRoC Sequence | |||||
|---|---|---|---|---|---|---|---|
| repr. | V101 | V102 | V103 | V201 | V202 | V203 | |
| V+I+G | CT | 0.024 | 0.014 | 0.011 \mathbf{0 . 0 1 1} 0.011 | 0.012 | 0.010 | 0.010 \mathbf{0 . 0 1 0} 0.010 |
| DT | 0.016 | 0.024 | 0.018 | 0.009 \mathbf{0 . 0 0 9} 0.009 | 0.018 | 0.033 | |
| V+G | CT | 0.011 | 0.013 \mathbf{0 . 0 1 3} 0.013 | 0.012 | 0.009 \mathbf{0 . 0 0 9} 0.009 | 0.008 \mathbf{0 . 0 0 8} 0.008 | 0.012 |
| DT | 0.010 \mathbf{0 . 0 1 0} 0.010 | 0.025 | 0.024 | 0.010 | 0.012 | 0.029 | |
| I + G \mathrm{I}+\mathrm{G} I+G | CT | 0.062 | 0.102 | 0.117 | 0.112 | 0.164 | 0.363 |
| DT | 0.139 | 0.137 | 0.138 | 0.138 | 0.138 | 0.139 | |
| V+I | CT | 0.039 | 0.022 | 0.014 | 0.065 | 0.030 | 0.015 |
| DT | 0.081 | 0.106 | 0.030 | 0.064 | 0.022 | 0.031 |
表VI: 不同传感器模态贡献的消融研究。误差度量是 A T E R \mathrm{ATE}_{\mathrm{R}} ATER(单位:度)。V: 视觉,I: 惯性,G: 模拟GPS。每个序列的最佳值用粗体表示。
| Sensors | Traj. | EuRoC Sequence | |||||
|---|---|---|---|---|---|---|---|
| repr. | V101 | V102 | V103 | V201 | V202 | V203 | |
| V + I + G \mathrm{V}+\mathrm{I}+\mathrm{G} V+I+G | CT | 5.5 | 2.1 | 2.3 | 0.8 \mathbf{0 . 8} 0.8 | 0.7 \mathbf{0 . 7} 0.7 | 0.6 \mathbf{0 . 6} 0.6 |
| DT | 5.6 | 2.4 | 2.7 | 1.0 | 0.8 | 1.1 | |
| V + G \mathrm{~V}+\mathrm{G} V+G | CT | 5.5 | 2.3 | 2.5 | 1.1 | 0.8 | 1.2 |
| DT | 5.6 | 2.3 | 2.7 | 1.1 | 0.8 | 0.9 | |
| I + G \mathrm{I}+\mathrm{G} I+G | CT | 10.5 | 6.3 | 7.6 | 11.0 | 11.0 | 9.4 |
| DT | 12.3 | 7.7 | 8.8 | 11.8 | 11.8 | 10.6 | |
| V + I \mathrm{~V}+\mathrm{I} V+I | CT | 5.4 \mathbf{5 . 4} 5.4 | 2.0 \mathbf{2 . 0} 2.0 | 2.2 \mathbf{2 . 2} 2.2 | 0.9 | 0.8 | 0.6 \mathbf{0 . 6} 0.6 |
| DT | 5.5 | 2.2 | 2.8 | 1.0 | 0.8 | 1.2 |
B. 使用室外飞行机器人进行实际GPS实验
该数据集由[27]提供,包含一个配备时间同步的VI传感器(立体摄像头和IMU)以及GPS接收器的飞行机器人在室外飞行的数据。GPS测量值为5 Hz。我们仅使用左摄像头的图像。地面真值位置由Leica全站仪提供。图3展示了该数据集的第一条轨迹。 A T E P \mathrm{ATE}_{P} ATEP和时间偏移估计值见表VII。对于连续时间的情况,我们使用了6阶B样条和10 Hz的控制节点频率。正如在第IV-A节中的结果所示,这些值适用于表示飞行机器人轨迹。实验结果确认了第IV-A节的发现,当传感器时间同步时,两个轨迹表示方法产生相似的结果,如 A T E P \mathrm{ATE}_{P} ATEP值和相机-IMU时间偏移估计值相似所示。
C. 室外轨迹:地面机器人
此实验评估了地面机器人上的轨迹,该机器人配备了时间同步的VI传感器(单目摄像头和IMU)和GPS天线。GPS测量值为5 Hz。3D位置的地面真值由RTKGPS系统提供。图4显示了机器人走过的轨迹。为了研究B样条阶数和控制点频率的影响,我们进行了阶数为5、6和7的实验,并且控制节点频率分别为10、20、100 Hz。无论是连续时间还是离散时间的表示方法,均产生了类似的ATE
P
_{P}
P值,如表VIII所示。所有配置的估计时间偏移值在表VIII中也表现得相似。

图 3: 户外飞行机器人实验中序列 1 飞行轨迹的 XY 视图。
表VII: 在室外飞行机器人数据集上,连续时间和离散时间方法的比较。 A T E P \mathrm{ATE}_{P} ATEP单位为米, t i c t_{i}^{c} tic单位为毫秒。每个序列的最佳 A T E P \mathrm{ATE}_{P} ATEP值用粗体表示。
| Err. metric | Traj. repr. | Seq. 1 | Seq. 2 |
|---|---|---|---|
| ∗ A T E P [ m ] { }^{*} \mathbf{A T E}_{\mathbf{P}}[\mathbf{m}] ∗ATEP[m] | CT | 0.39 \mathbf{0 . 3 9} 0.39 | 0.50 \mathbf{0 . 5 0} 0.50 |
| DT | 0.60 | 0.86 | |
| t i c [ m s ] \mathbf{t}_{\mathbf{i}}^{\mathbf{c}}[\mathbf{m s}] tic[ms] | CT | 0.4 | 0.6 |
| DT | 0.4 | 0.4 | |
| t i g [ m s ] \mathbf{t}_{\mathbf{i}}^{\mathbf{g}}[\mathbf{m s}] tig[ms] | CT | -87.0 | -118.0 |
| DT | -81.0 | -119.0 |
在连续时间情况下,使用6阶B样条和10 Hz的控制节点频率时, t i c t_{i}^{c} tic和 t i g t_{i}^{g} tig分别为-1.5毫秒和-26.0毫秒。对于离散时间情况,它们分别为-0.8毫秒和-36.3毫秒。这些结果表明,飞行机器人实验中的发现同样适用于地面机器人的情况。
V. 结论
本研究的目标是比较基于视觉的连续时间与离散时间SLAM公式,以指导从业人员在SLAM算法开发中的选择。我们在一个硬件环回仿真环境中进行了消融实验和对比研究,且拥有地面真值数据。关于B样条控制节点阶数和频率的消融研究表明,必须使用6阶B样条并且控制节点频率至少为10 Hz,以准确估计相机-IMU的时间偏移。对比研究的目的是比较具有不同相机-IMU时间延迟的连续时间与离散时间轨迹表示方法。我们发现,当相机与IMU时间同步时,两种表示方法产生相似的结果。而当两个测量流之间存在延迟时,连续时间表示能够准确恢复时间偏移估计,从而产生较低的ATE。相比之下,离散时间公式在估计时间偏移时表现不佳,尤其是在机器人高速运动时,导致较高的ATE。
图4: 地面机器人所行驶轨迹的 X Y XY XY视图。
表VIII: 在室外地面机器人数据集上,连续时间与离散时间方法的比较。误差度量是 A T E P \mathrm{ATE}_{P} ATEP,单位为米。每个序列的最佳值用粗体表示。
| Freq. [ H z ] [\mathbf{H z}] [Hz] | Order | |||
|---|---|---|---|---|
| 5 \mathbf{5} 5 | 6 \mathbf{6} 6 | 7 \mathbf{7} 7 | ||
| 20 | 1.93 | 0.92 | 0.93 | |
| 100 | 0.95 | 0.99 | ||
| DT | 0.87 |
这些结果的主要原因在于,在估计相机-IMU时间偏移时所需的假设——即在连续相机帧之间,相机运动的速度是恒定的——并不总是成立。硬件环回仿真实验的结果与实际数据集上包含飞行机器人和地面机器人数据的实验结果一致。此外,我们在消融研究中评估了每种传感器模态的贡献。我们发现,在EuRoC数据集中,最重要的传感器模态是视觉。在大多数序列中,通过使用噪声模拟GPS测量结果将从COLMAP获得的相机轨迹对齐到重力对齐框架,得到最低的ATE P _{P} P值。加入惯性测量并未带来显著的优势。
VI. 致谢
作者感谢Torsten Sattler和Antonio Loquercio的有益讨论,感谢Fixposition团队提供的地面机器人数据集。
REFERENCES
[1] C. Cadena, L. Carlone, H. Carrillo, Y. Latif, D. Scaramuzza, J. Neira, I. D. Reid, and J. J. Leonard, “Past, present, and future of simultaneous localization and mapping: Toward the robust-perception age,” IEEE Trans. Robot., vol. 32, no. 6, pp. 1309-1332, 2016.
[2] H. Durrant-Whyte and T. Bailey, “Simultaneous localization and mapping: part i,” IEEE robotics & automation magazine, vol. 13, no. 2, pp. 99-110, 2006.
[3] T. Qin and S. Shen, “Online temporal calibration for monocular visualinertial systems,” in IEEE/RSJ Int. Conf. Intell. Robot. Syst. (IROS), 2018.
[4] C. Forster, L. Carlone, F. Dellaert, and D. Scaramuzza, “On-manifold preintegration for real-time visual-inertial odometry,” IEEE Trans. Robot., vol. 33, no. 1, pp. 1-21, 2017.
[5] P. Furgale, T. D. Barfoot, and G. Sibley, “Continuous-time batch estimation using temporal basis functions,” in IEEE Int. Conf. Robot. Autom. (ICRA), 2012.
[6] H. Ovrén and P.-E. Forssén, “Trajectory representation and landmark projection for continuous-time structure from motion,” Int. J. Robot. Research, vol. 38, no. 6, pp. 686-701, 2019.
[7] E. Mueggler, G. Gallego, H. Rebecq, and D. Scaramuzza, “Continuoustime visual-inertial odometry for event cameras,” IEEE Trans. Robot., vol. 34 , no. 6 , pp. 1425-1440, Dec. 2018.
[8] P. Furgale, J. Rehder, and R. Siegwart, “Unified temporal and spatial calibration for multi-sensor systems,” in IEEE/RSJ Int. Conf. Intell. Robot. Syst. (IROS), 2013.
[9] W. Ding, W. Gao, K. Wang, and S. Shen, “An efficient b-spline-based kinodynamic replanning framework for quadrotors,” IEEE Trans. Robot., vol. 35, no. 6, pp. 1287-1306, 2019.
[10] A. J. Yang, C. Cui, I. A. Bârsan, R. Urtasun, and S. Wang, “Asynchronous multi-view slam,” IEEE Int. Conf. Robot. Autom. (ICRA), 2021.
[11] H. Ovrén and P.-E. Forssén, “Spline error weighting for robust visualinertial fusion,” in IEEE Conf. Comput. Vis. Pattern Recog. (CVPR), 2018.
[12] C. Sommer, V. Usenko, D. Schubert, N. Demmel, and D. Cremers, “Efficient derivative computation for cumulative b-splines on lie groups,” in IEEE Conf. Comput. Vis. Pattern Recog. (CVPR), 2020.
[13] S. Anderson, F. Dellaert, and T. D. Barfoot, “A hierarchical wavelet decomposition for continuous-time SLAM,” in IEEE Int. Conf. Robot. Autom. (ICRA), 2014.
[14] S. Anderson, T. D. Barfoot, C. H. Tong, and S. Särkkä, “Batch nonlinear continuous-time trajectory estimation as exactly sparse gaussian process regression,” Autonomous Robots, vol. 39, no. 3, pp. 221-238, 2015.
[15] D. Hug and M. Chli, “On conceptualizing a framework for sensor fusion in continuous-time simultaneous localization and mapping,” in 3D Vision (3DV), 2020.
[16] W. Lee, K. Eckenhoff, P. Geneva, and G. Huang, “Intermittent gps-aided vio: Online initialization and calibration,” in IEEE Int. Conf. Robot. Autom. (ICRA), 2020.
[17] J. L. Schönberger and J.-M. Frahm, “Structure-from-motion revisited,” in IEEE Conf. Comput. Vis. Pattern Recog. (CVPR), 2016.
[18] C. de Boor, A practical guide to splines. Springer Verlag New York, 2001.
[19] K. Qin, “General matrix representations for B-splines,” The Visual Computer, vol. 16, no. 3-4, pp. 177-186, 2000.
[20] H. Sommer, J. R. Forbes, R. Siegwart, and P. Furgale, “Continuoustime estimation of attitude using b-splines on lie groups,” Journal of Guidance, Control, and Dynamics, vol. 39, no. 2, pp. 242-261, 2016.
[21] A. Haarbach, T. Birdal, and S. Ilic, “Survey of higher order rigid body motion interpolation methods for keyframe animation and continuoustime trajectory estimation,” in
3
D
3 D
3D Vision (3DV), 2018.
[22] S. Umeyama, “Least-squares estimation of transformation parameters between two point patterns,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 13, no. 4, 1991.
[23] T. Qin, P. Li, and S. Shen, “VINS-Mono: A robust and versatile monocular visual-inertial state estimator,” IEEE Trans. Robot., vol. 34, no. 4, pp. 1004-1020, 2018.
[24] Z. Zhang and D. Scaramuzza, “A tutorial on quantitative trajectory evaluation for visual(-inertial) odometry,” in IEEE/RSJ Int. Conf. Intell. Robot. Syst. (IROS), 2018.
[25] A. Agarwal, K. Mierle, and Others, “Ceres solver,” http://ceres-solver. org
[26] M. Burri, J. Nikolic, P. Gohl, T. Schneider, J. Rehder, S. Omari, M. W. Achtelik, and R. Siegwart, “The EuRoC micro aerial vehicle datasets,” Int. J. Robot. Research, vol. 35, no. 10, pp. 1157-1163, 2015.
[27] J. Surber, L. Teixeira, and M. Chli, “Robust Visual-Inertial Localization with Weak GPS Priors for Repetitive UAV Flights,” in IEEE Int. Conf. Robot. Autom. (ICRA), 2017.
Manuscript received: September, 9, 2021; Revised December, 1, 2021; Accepted December, 27, 2021.
This paper was recommended for publication by Editor Javier Civera upon evaluation of the Associate Editor and Reviewers’ comments.
This work was supported by the National Centre of Competence in Research (NCCR) Robotics through the Swiss National Science Foundation (SNSF) and the European Union’s Horizon 2020 Research and Innovation Programme under grant agreement No. 871479 (AERIAL-CORE) and the European Research Council (ERC) under grant agreement No. 864042 (AGILEFLIGHT).The authors are with the Robotics and Perception Group, Department of Informatics, University of Zurich, and Department of Neuroinformatics, University of Zurich and ETH Zurich, Switzerland http://rpg.ifi.uzh.ch). cioffi@ifi.uzh.ch
Digital Object Identifier (DOI): see top of this page. ↩︎
























 1052
1052

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










