【Unity 手写PBR】Build-in管线：实现直接光部分

写在前面

前期积累：

GAMES101作业7提高-实现微表面模型你需要了解的知识

【技术美术图形部分】PBR直接光部分：Disney原则的BRDF和次表面散射模型

 【技术美术图形部分】PBR全局光照：理论知识补充

算是对光照模型计算的查漏补缺吧，因此会在每一步加入一些自己遇到的问题和解决方案。 

---

1 声明材质属性

关于Metal-Roughness和Specualr-Glossiness工作流贴图区别，概述一下大概是，

• 金属工作流：BaseColor + Roughness + Metallic   + AmbientOcclusion + normal + height
• 高光工作流：   Diffuse + Glossiness + Specular    + AmbientOcclusion + normal + height

前三个是特有贴图，后面AO/法线/高度图是两个流程都可以加入的。我这里造的是PBR金属工作流的轮子，那就选前者，话不多说，准备传入！

1.1 Unity Standard shader

Standard Shader传参方式：

• Albedo：传入_MainTex和_Color
• Metallic：传入_MetallicTex和_MetallicStrength
• Smoothness：是Unity定义的光滑度，光滑度+粗糙度=1，而_SmoothTex来自于_MainTex的Alpha通道or_MetallicTex的Alpha通道
• NormalMap：法线
• HeightMap：高度图，用以视差
• Occlusion：AO贴图

1.2 我传入的参数

考虑到URP下传入的也是roughness，这里就不按照Standard的做法了，还是传入Roughness的，同时高度图改成Parallax吧，更能体现他的用途，先不把Metal和Roughness合并到一张贴图里，后面改到URP的时候再合一下，最后加上一个自发光贴图：

        _MainMap ("BaseMap", 2D) = "white" {}                       // 反照率
        _Color ("Color", Color) = (1, 1, 1, 1)                      // 颜色
        
        _RoughnessMap ("RoughnessMap", 2D) = "white" {}             // 粗糙度
        [Gamma]_Roughness ("Roughness", Range(0, 1)) = 0                   // 粗糙度强度

        _MetallicMap ("MetallicMap", 2D) = "white" {}               // 金属度
        [Gamma]_Metallic ("Metallic", Range(0, 1)) = 0                     // 金属度强度

        _NormalMap ("NormalMap", 2D) = "bump" {}                    // 法线贴图
        _Normal ("Normal", Range(0, 1)) = 0                         // 法线强度

        _ParallaxMap ("HeightMap", 2D) = "white" {}                 // 高度/视差贴图
        _Parallax ("Height Scale", Range(0, 1)) = 0                 // 强度

         _OcclusionMap ("AOMap", 2D) = "white" {}                   // AO
        _Occlusion ("AO", Range(0, 1)) = 0                          // 强度

        _EmissionMap ("EmissionMap", 2D) = "white" {}               // 自发光贴图
        _EmissionColor ("EmissionColor", Color) = (1, 1, 1, 1)      // 自发光颜色

2 进行必要的信息计算

我们在片元着色器实现光照计算，需要提前计算出一些方向值，点积值。

救命，突然发现光照只要一复杂，vertex shader 和 fragment shader传递参数就需要更加严谨了。顶点的信息在vertex shader和在fragment shader是不同的，特别是法线，

• 顶点着色器：法线是每个顶点都有的
• 片元着色器：会把顶点传递过的参数在三角面片内部插值，相当于平滑了法线信息，因此着色时需要再次将传入的法线归一化处理

所以说，记得每个方向相关的变量最好都在片元着色器中归一化处理。

        i.worldNormal = normalize(i.worldNormal);
        float3 lightDir = normalize(_WorldSpaceLightPos0.xyz);
        float3 viewDir = normalize(_WorldSpaceCameraPos - i.worldPos.xyz);
        float3 lightColor = _LightColor0.rgb;
        float3 halfVector = normalize(lightDir+viewDir); // 半角
        float PI = 3.1415926;

        // 点积值
        float ndotl = max(saturate(dot(i.worldNormal, lightDir)), 0.0001); //防止除零
        float ndotv = max(saturate(dot(i.worldNormal, viewDir)), 0.0001);
        float vdoth = max(saturate(dot(viewDir, halfVector)), 0.0001);
        float ldoth = max(saturate(dot(lightDir, halfVector)), 0.0001);
        float ndoth = max(saturate(dot(i.worldNormal, halfVector)), 0.0001);

除去这些参与计算的信息，还有法线纹理应用的信息也需要补充完整。

以及采样贴图：

        float3 albedo = tex2D(_MainMap, i.uv) * _Color.rgb;       // 反照率
        float3 metallic = tex2D(_MetallicMap, i.uv) * _Metallic;  // 金属度

3 漫反射 Diffuse

漫反射有两个，

• Disney方法
• Lambert方法

再回来写shader，为了让shader看上去更加整洁，这里另开了一个文件把计算公式都封装起来，放到了一个cginc文件，在shader中调用。

3.1 Disney漫反射

计算： 

// Disney_Diffuse
inline float3 Diffuse_Disney(float roughness, float ndotv, float ndotl, float ldoth){
    float PI = 3.1415926;
    float FD90 = 0.5 + 2 * ldoth * ldoth * roughness;
    float FdV = 1 + (FD90 - 1) * pow((1 - ndotv), 5);
    float FdL = 1 + (FD90 - 1) * pow((1 - ndotl), 5);
    // return ((1 / PI) * FdV * FdL); // (1/PI)会让着色变黑很多，这里不除以PI
    return FdV * FdL;
}

表面粗糙度取值 

计算前需要准备好计算需要的粗糙度，

        // 粗糙度
        float roughness = pow(_Roughness,2); // roughness映射成了roughness^2
        float lerpSquareRoughness = pow(max(0.002,roughness),2); // 计算D项时使用，给一个0.002不至于完全没有高光
        float squareRoughness = pow(roughness,2); // Roughness^2

关于表面粗糙度的取值，我之前的文章就有写到：

所以这里粗糙度其实是把传入的参数进行了平方处理，以后的公式中涉及到的roughness实际上是我们的_Roughness^2。另外还额外计算了一个lerp过的roughness^2，这是为后续计算法线分布函数D项做铺垫。

是否除PI？

关于除PI问题，由于我是在Build-in下实现的，对比的话其实就是跟Standard Shader做对比，希望实现的尽可能贴近它的效果吧！参考文章中这么描述的：

截图自 如何在Unity中造一个PBR Shader轮子 - 知乎 (zhihu.com)

尝试一下，除PI前后对比（这里加上了高光项，不仅仅只有diffuseColor）：

除PI

不除PI

整体Diffuse会暗淡很多，这里我们也不除PI，但注意，Diffuse如果没有除PI，为了保证能量守恒，高光项是需要乘上一个PI的，后面会讲到。

3.2 2种漫反射效果对比

另一种就是Lambert了，UE也用的是这个~对比一下的话，我们只返回DiffuseColor，从左到右(Roughness,Metallic)依次是(1,0)(1,1)(0,0)(0,1)：

Disney Diffuse

Lambert Diffuse

说实话，这样看上去并没有什么区别，，，我之前总结的文章中有提到：

目前认为需要更加复杂的材质才能体现Disney和Diffuse的区别，就先进入下一节吧。

4 法线分布 D项

法线分布函数可不止一种：

【基于物理的渲染（PBR）白皮书】（四）法线分布函数相关总结 - 知乎 (zhihu.com)

4.1 标准的GGX分布

shader中实现：

// D_GGX
inline float DistributionGGX(float ndoth, float squareRoughness){
    float PI = 3.1415926;
    float m = ndoth * ndoth * (squareRoughness - 1) + 1;
    return squareRoughness / ((m * m) * PI);
}

4.2 UE移动端的优化方案

参考：

UE4 Forward PBR to Mobile PBR - 知乎 (zhihu.com)

UE4 移动端PBR模型浅析 - 知乎 (zhihu.com)

【基于物理的渲染（PBR）白皮书】（四）法线分布函数相关总结 - 知乎 (zhihu.com)

这部分算是一个拓展？感觉按部就班的实现PBR稍微有点枯燥了hhh，毕竟直接光照说来说去就是那老三样D、F、G，加入点不一样的。这一小节其实想体现的是UE Mobile PBR针对移动端对D项计算进行的优化，前提是我们需要知道UE移动端的Specular BRDF并不是真正的PBR了，简化成了：

截图自 UE4 移动端PBR模型浅析 - 知乎 (zhihu.com)

这里的D项的NDF还是用的GGX分布，但是实现做了很多优化手段。比如上述正常实现用的是float，这里使用半精度浮点数half节省储存和计算，需要改变原始方程，具体见下面的代码注释。

我这样仅仅在Unity里对比不一定严谨，但只要知道修改的内容是什么就好了：

• PC GPU始终按照高精度float32位计算，移动端考虑性能的话会尽量使用half
• half带来了计算公式的误差，因此需要修改原始计算方法

取上述方法，完整代码如果在Unity写的话，会是：

inline half MobileGGX(half NoH, half3 H, half3 N, half roughness){
    float PI = 3.1415926;
    roughness = lerp(0.002,1,roughness);
    float3 NxH = cross(N, H);
    float oneMinusNoHSqr = dot(NxH, NxH); // (nxm)^2 = 1 - (n·m)^2 近似
    // float oneMinusNoHSqr = 1 - NoH * NoH;
    float n = NoH * roughness;
    float p = roughness / (oneMinusNoHSqr + n * n);
    return p * p / PI;
}

4.3 二者简单对比

标准GGX

优化GGX

关于D项的探讨就到这里。

5 阴影遮挡 G项

【基于物理的渲染（PBR）白皮书】（五）几何函数相关总结 - 知乎 (zhihu.com)

计算G项实际上就是一个选择几何函数的过程。关于几何函数模型的选择，SIGGRAPH 2014前后算是个转折，这里就提取三个比较常见的方案，然后三者效果对比对比。

5.1 Disney方案

SSIGGRAPH 2012，Disney提出的Smith GGX几何项表达式为：

截图自 【基于物理的渲染（PBR）白皮书】（五）几何函数相关总结 - 知乎 (zhihu.com)

重映射了粗糙度减少光泽表面的极端增益，使得粗糙变化更加平滑！

Shader里写一下：

// Disney_G
// G1
inline float SmithG_GGX(float ndotv, float roughness){
    float r = 0.5 + roughness / 2.0f;
    float m = r * r + (1 - r * r) * ndotv * ndotv;
    return 2.0f * ndotv / (ndotv + sqrt(m));
}
// G2
inline float Disney_G(float ndotv, float ndotl, float roughness){
    float ggx1 = SmithG_GGX(ndotl, roughness);
    float ggx2 = SmithG_GGX(ndotv, roughness);
    return ggx1 * ggx2;
}

5.2 UE4 近似Smith方案

这里主要是UE4采用的Schlick近似Smith方案，直接截图我文章内容：

粗糙度映射参考了Disney的，Shader里写一下：

// UE_G
inline float SchlickGGX(float ndotv, float roughness){
    float r = roughness + 1;
    float m = r * r / 8;
    float k = ndotv / ndotv * (1 - m) + m;
    return ndotv / k;
}
inline float UE_G(float ndotv, float ndotl, float roughness){
    float ggx1 = SchlickGGX(ndotl, roughness);
    float ggx2 = SchlickGGX(ndotv, roughness);
    return ggx1 * ggx2;
}

5.3 Unity Smith联合方案(V项)

SIGGRAPH 2014提出了The Smith Joint Masking-Shadowing Function，算是一个转折！游戏和电影业界都转向了这个Smith联合遮蔽阴影函数，拿引擎来说，UE4和Unity都做了一定的优化。

这里就拿Unity方案举例，其实Unity的PBR划分了几个档次的，每个Level对应不同的性能需求，或许移动端、HDRP等等采用的是不同的G项，这里我不是很能分清具体是怎么划分的。。。扒拉UnityStandardBRDF.cginc源码的时候看到这个实现方法：

// Ref: http://jcgt.org/published/0003/02/03/paper.pdf
inline float SmithJointGGXVisibilityTerm (float NdotL, float NdotV, float roughness)
{
#if 0
    // Original formulation:
    //  lambda_v    = (-1 + sqrt(a2 * (1 - NdotL2) / NdotL2 + 1)) * 0.5f;
    //  lambda_l    = (-1 + sqrt(a2 * (1 - NdotV2) / NdotV2 + 1)) * 0.5f;
    //  G           = 1 / (1 + lambda_v + lambda_l);

    // Reorder code to be more optimal
    half a          = roughness;
    half a2         = a * a;

    half lambdaV    = NdotL * sqrt((-NdotV * a2 + NdotV) * NdotV + a2);
    half lambdaL    = NdotV * sqrt((-NdotL * a2 + NdotL) * NdotL + a2);

    // Simplify visibility term: (2.0f * NdotL * NdotV) /  ((4.0f * NdotL * NdotV) * (lambda_v + lambda_l + 1e-5f));
    return 0.5f / (lambdaV + lambdaL + 1e-5f);  // This function is not intended to be running on Mobile,
                                                // therefore epsilon is smaller than can be represented by half
#else
    // Approximation of the above formulation (simplify the sqrt, not mathematically correct but close enough)
    float a = roughness;
    float lambdaV = NdotL * (NdotV * (1 - a) + a);
    float lambdaL = NdotV * (NdotL * (1 - a) + a);
#endif
}

使用V项的渲染方程

根据上面的公式，似乎Unity计算的不只是G项，而是一个V项，V = G * 某个系数，联系BRDF方程：

Unity这里似乎是计算了剩下的系数*G，组成了V项，所以最后的话就不需要考虑分母的系数了，于是整个渲染方程就成了：

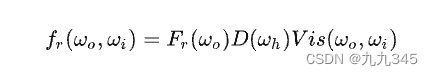
这是彻底看懂PBR/BRDF方程 - 知乎 (zhihu.com)对它的解释，其实就是引擎的小trick：

而且上述代码有两个计算方法，

• 方法1：更精确，涉及到sqrt()开方，计算昂贵，默认为0（关闭状态）
• 方法2：把a^2省略了，计算简化，开销也不大

行，姑且就按照这个写一个出来：

// Unity_G
// SmithJointGGXVisibilityTerm()
inline float Unity_G(float ndotv, float ndotl, float roughness){
    // 简化了a^2但效果近似
    float a = roughness;
    float lambdaV = ndotl * (ndotv * (1 - a) + a);
    float lambdaL = ndotv * (ndotl * (1 - a) + a);
    return 0.5f / (lambdaV + lambdaL + 1e-5f);
}

5.4 三者对比

Disney方案

UE4方案

Unity联合方案

我们暂时忽略为什么Unity方案下背面是亮的，因为这仅仅是输出计算的G项，没有做一个n·l处理。你会发现，Unity方案下的效果相比于前两个，边缘（准确说是掠射角）有一个增强亮度的效果。

6 菲涅尔 F项

6.1 完整方程

又又又来了菲涅尔方程——描述了不同入射光下反射光所占的比例。就是说，之前实现过超级复杂版的菲涅尔方程：GAMES101作业5-从头到尾理解代码&Whitted光线追踪，做101作业的时候就参照原本的菲涅尔表达式计算了菲涅尔项，

代码这里就不放了。

6.2 两种近似计算法

Fresnel-Schlick近似法

实际项目中要是用这个复杂的方法计算菲涅尔项，，代价太大了！为了节省计算开销，就又要找近似方法了，其中Schlick提出的近似法使用最为广泛：

UE4的加速版本

用exp2做了近似计算，速度会更快。

6.3 讨论金属与非金属的F0

参考：UE4基于物理的着色(二) 菲涅尔反射 - 知乎 (zhihu.com)

上述近似计算式子中，F0表示介质材质的基础反射率。根据F0的不同可以把介质分为3类，

• 电介质：玻璃、木头、皮肤等等，这些材质的F0通常很低，且不用考虑表面颜色
• 金属：金属的F0都挺高，通常大于0.5，而且会有金属表面颜色
• 半导体：介于电介质和金属，渲染中很少涉及

半导体我们忽略吧，那姑且把材质分为金属和非金属，

• 金属的F0：RGB值
• 非金属的F0：标量

非金属F0：0.04

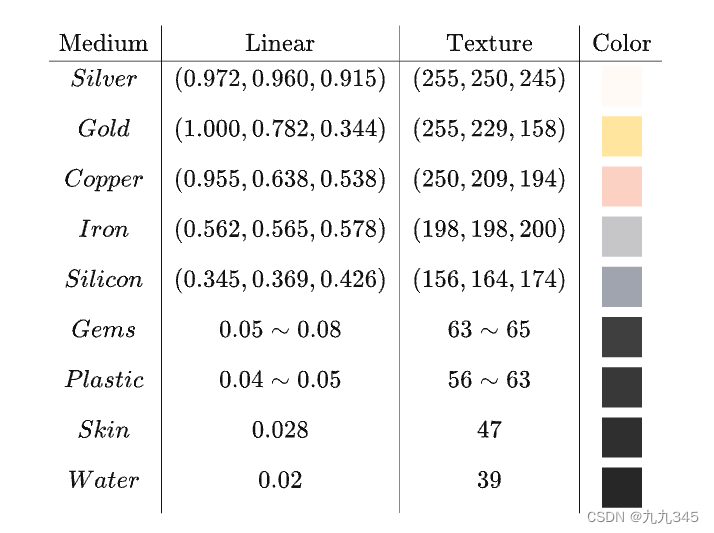
通过下面表格可以观察到，大部分电介质Specular值在线性空间下就是在0.04附近，所以我们干脆直接默认电介质的F0就是0.04。

截图自 UE4基于物理的着色(二) 菲涅尔反射 - 知乎 (zhihu.com)

金属材质F0

PBR中我们认为金属没有漫反射，漫反射始终认为是黑色，之所以看到有颜色是因为它的反射。而且观察上面的表格，你会发现，金属的Specular几乎等于他的表面颜色，那我们就直接拿金属的表面颜色当作F0就行。

6.4 Unity计算方案

F0

如果想用同一个公式计算两种材质的菲涅尔项，就需要某一个集合去计入F0。啊，既然牵扯了颜色，那要提一提我们最开始定义的几个参数，

• albedo：采样反照率*_Color
• metallic：采样金属度贴图*metallicStrength

对于F0项的计算，Unity源码如下：

inline half3 DiffuseAndSpecularFromMetallic (half3 albedo, half metallic,out half3 specColor, out half oneMinusReflectivity
) {
	specColor = lerp(unity_ColorSpaceDielectricSpec.rgb, albedo, metallic);
	oneMinusReflectivity = OneMinusReflectivityFromMetallic(metallic);
	return albedo * oneMinusReflectivity;
}

其中，unity_ColorSpaceDielectricSpec是Unity定义的一个绝缘体（非金属的的所有材料）的specular颜色，线性空间下默认为fixed4(0.04,0.04,0.04,0.96)（参考自参考文章），就是上面那个定值0.04.

其中，specColor就是在计算F0，metallic=1返回albedo，metallic=0，返回0.04（可以认为0.04*fixed4(1,1,1,1)黑色）。这符合上面我们讨论的金属和非金属的F0取值！

F项

直接参照的是Fresnel-Schlick近似法。

shader中写一下：

        float3 F0 = lerp(unity_ColorSpaceDielectricSpec.rgb, albedo, metallic);
        F = Fresnel(F0, ldoth);

// 菲涅尔项 F
// Unity这里传入的是ldoth,而非vdoth
inline float3 Fresnel(float3 F0, float cosA){
    float a = pow((1 - cosA), 5);
    return (F0 + (1 - F0) * a);
}

这里要注意了，Unity选择传入的值是dot(l,h)，是一种优化手段。详细解释如下：

传送门 https://zhuanlan.zhihu.com/p/68025039

6.5 效果

这里是对比的Unity和UE的，其实动态更能体现出F项的作用：当场景中在光线垂直打在表面（光线处于掠射角时），非金属表面会突然变亮。这很符合菲涅尔现象——平静的湖面垂直能看到湖底，远处的湖面却有天空的倒影。

其实真的要看区别看不出什么区别，看到参考文章说，F实际上是把金属和非金属区分开，金属高光带有Albedo但非金属不带。

7 漫反射系数kd

漫反射系数需要考虑镜面反射的影响，而镜面反射的ks就是F，因此只需要考虑以下kd的取值就行！

7.1 F项对kd的影响

正常来讲，F项是菲涅尔项，就是被反射的，那么，一步一步看的话：

• 镜面反射剩下的就是漫反射吸收的部分：（1 - F）
• 金属不产生漫反射，你可以理解为剔除掉金属吸收的部分，因此叠加之后有(1 - F)(1 - metallic)

那么最后的结果就是，

kd = (1 - F) * (1 - metallic);

7.2 Unity如何计算kd

DiffuseAndSpecularFromMetallic

Unity中计算kd是在DiffuseAndSpecularFromMetallic完成的，Unity源码：

inline half OneMinusReflectivityFromMetallic(half metallic) {
	// We'll need oneMinusReflectivity, so
	//   1-reflectivity = 1-lerp(dielectricSpec, 1, metallic)
	//                  = lerp(1-dielectricSpec, 0, metallic)
	// store (1-dielectricSpec) in unity_ColorSpaceDielectricSpec.a, then
	//	 1-reflectivity = lerp(alpha, 0, metallic)
	//                  = alpha + metallic*(0 - alpha)
	//                  = alpha - metallic * alpha
	half oneMinusDielectricSpec = unity_ColorSpaceDielectricSpec.a;
	return oneMinusDielectricSpec - metallic * oneMinusDielectricSpec;
}

inline half3 DiffuseAndSpecularFromMetallic (half3 albedo, half metallic,out half3 specColor, out half oneMinusReflectivity
) {
	specColor = lerp(unity_ColorSpaceDielectricSpec.rgb, albedo, metallic);
	oneMinusReflectivity = OneMinusReflectivityFromMetallic(metallic);
	return albedo * oneMinusReflectivity;
}

按照他的思路，我们也写一个：

float3 kd = (1 - metallic) * unity_ColorSpaceDielectricSpec.a;

就是(1 - metallic) * 0.96！

为什么！少了一个(1 - F) 项呢？来，我们对比一下：

Unity方案

(1 - F)(1 - metallic)方案

天，你会发现，二者几乎区别。这就是下一个想讨论的点了：

7.3 讨论1-F项

本小部分参考自：彻底看懂PBR/BRDF方程 - 知乎 (zhihu.com) 

Unity中直接忽略了1-F，是因为考虑到F值比较大的时候，都是在边缘区域，镜面反射很强，漫反射相对弱，而kd是漫反射系数，所以说完全可以直接忽略掉1-F项。

这给全局光照计算带来很大的便利，渲染方程就变成了：

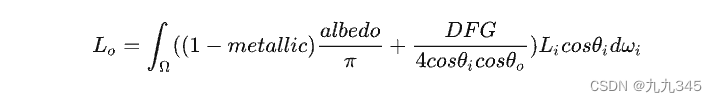
这里用的是Lambert计算漫反射。那么带来了怎样的便利？省略掉1-F项后，漫反射就完全跟方向无关了，对后期烘焙lightmap、VXGI计算间接光漫反射的时候非常友好。

8 整合直接光照

最终合起来，所有的计算都选取Unity的方案，那么最终：

        specular = D*F*G; // BRDF高光项
        float3 kd = (1 - metallic) * unity_ColorSpaceDielectricSpec.a; // 漫反射系数，需要根据F项改动，保持能量守恒
        float3 diffuseColor = kd * albedo * diffuse * lightColor * ndotl;
        float3 specularColor = specular * lightColor * ndotl * UNITY_PI; // 考虑能量守恒

        // 结果
        float3 directLight = diffuseColor + specularColor;

9 效果

参考如何在Unity中造一个PBR Shader轮子的对比方法，由于是在Unity里实现的当然要有个对比啦，手写PBR才有意义。

我也来给个对比：

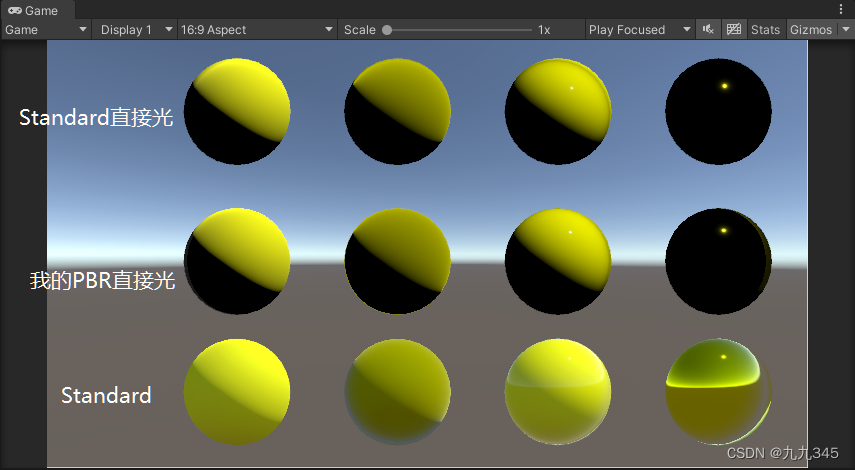
可喜可贺。。。第一二排看上去差不多，，，orz

又过去了半天，接下来要实现间接光部分啦！

参考

好像没写太全，有的在文中就标注啦！

如何在Unity中造一个PBR Shader轮子 - 知乎 (zhihu.com)

UE4 移动端PBR模型浅析 - 知乎 (zhihu.com)

UE4基于物理的着色(二) 菲涅尔反射 - 知乎 (zhihu.com)

Unity【基于物理的渲染(PBR)】 个人学习档案 - 知乎 (zhihu.com)