一.酉空间(10.5)
1.复线性空间上的内积

(1)概念:

(2)共轭线性:

2.酉空间(复内积空间)的概念:

3.酉空间的度量
(1)长度:

(2)夹角:

定理1(柯西-布尼亚科夫斯基-施瓦茨不等式,Cauchy-Buniakowsky-Schwarz Inequality):在酉空间 V V V中,对于任意向量 α , β α,β α,β,有 ∣ ( α , β ) ∣ ≤ ∣ α ∣ ∣ β ∣ ( 7 ) |(α,β)|≤|α||β|\qquad(7) ∣(α,β)∣≤∣α∣∣β∣(7)等号成立当且仅当 α , β α,β α,β线性相关

(3)正交:

(4)其他相关结论:
把复数 z z z的实部记为 R e z Re\,z Rez,虚部记为 I m z Im\,z Imz
推论1(三角形不等式):在酉空间 V V V中,有 ∣ α + β ∣ ≤ ∣ α ∣ + ∣ β ∣ ( ∀ α , β ∈ V ) ( 11 ) |α+β|≤|α|+|β|\,(∀α,β∈V)\qquad(11) ∣α+β∣≤∣α∣+∣β∣(∀α,β∈V)(11)
推论2(勾股定理):在酉空间 V V V中,若 α ⊥ β α⊥β α⊥β,则 ∣ α + β ∣ 2 = ∣ α ∣ 2 + ∣ β ∣ 2 ( 12 ) |α+β|^2=|α|^2+|β|^2\qquad(12) ∣α+β∣2=∣α∣2+∣β∣2(12)
用数学归纳法可以把勾股定理推广为:如果 α 1 , α 2 . . . α s α_1,α_2...α_s α1,α2...αs两两正交,那么 ∣ α 1 + α 2 + . . . + α s ∣ 2 = ∣ α 1 ∣ 2 + ∣ α 2 ∣ 2 + . . . + ∣ α s ∣ 2 ( 13 ) |α_1+α_2+...+α_s|^2=|α_1|^2+|α_2|^2+...+|α_s|^2\qquad(13) ∣α1+α2+...+αs∣2=∣α1∣2+∣α2∣2+...+∣αs∣2(13)
推论3:在酉空间 V V V中,对 α , β ∈ V α,β∈V α,β∈V,规定 d ( α , β ) : = ∣ α − β ∣ d(α,β):=|α-β| d(α,β):=∣α−β∣则 d d d是1个距离,从而酉空间 V V V对该距离成为1个度量空间
4.有限维酉空间中的标准正交基
命题1:在酉空间 V V V中,由两两相加的非零向量组成的集合是线性无关的
推论1:在 n n n维酉空间 V V V中,两两相加的非零向量的个数不超过 n n n
(1)正交规范集:

(2)正交基:

定理2: n n n维酉空间 V V V一定有标准正交基
(3)Gram矩阵:


(4)标准正交基的应用:
计算内积:
计算向量的坐标:
(5)酉矩阵:


定理3:设 η 1 , η 2 . . . η n η_1,η_2...η_n η1,η2...ηn是 n n n维酉空间 V V V上的1个标准正交基,向量组 β 1 , β 2 . . . β n β_1,β_2...β_n β1,β2...βn满足 ( β 1 , β 2 . . . β n ) = ( η 1 , η 2 . . . η n ) P ( 21 ) (β_1,β_2...β_n)=(η_1,η_2...η_n)P\qquad(21) (β1,β2...βn)=(η1,η2...ηn)P(21)则 β 1 , β 2 . . . β n β_1,β_2...β_n β1,β2...βn是 V V V的1个标准正交基当且仅当 P P P是酉矩阵
5.酉空间的同构
(1)概念:

(2)判定:
定理4:2个有限维酉空间同构的充要条件是它们的维数相同
推论1:设 V V V是 n n n维酉空间,则 V V V上的线性变换 σ σ σ是保距同构当且仅当 σ σ σ把 V V V的标准正交基映成标准正交基
定理6:设 V , V ′ V,V' V,V′都是酉空间,如果存在 V V V到 V ′ V' V′的1个那么满射 σ σ σ保持向量的内积不变,那么 σ σ σ是 V V V到 V ′ V' V′的1个保距同构,从而 V V V与 V ′ V' V′同构
推论1:设 V , V ′ V,V' V,V′都是 n n n维酉空间,如果存在 V V V到 V ′ V' V′的1个映射 σ σ σ保持向量的内积不变,那么 σ σ σ是 V V V到 V ′ V' V′的1个保距同构,从而 V V V与 V ′ V' V′同构
(3)性质:
定理5:设 V , V ′ V,V' V,V′都是酉空间,如果存在 V V V到 V ′ V' V′的1个映射 σ σ σ保持向量的内积不变,那么
( 1 ) σ (1)σ (1)σ保持向量的长度不变
( 2 ) σ (2)σ (2)σ是 V V V到 V ′ V' V′的1个线性映射
( 3 ) σ (3)σ (3)σ是单射
6.酉空间中的正交补与正交投影(10.5)
(1)正交补:
定理7:设 U U U是酉空间 V V V的1个有限维非零子空间,则 V = U ⊕ U ⊥ ( 22 ) V=U\oplus U^⊥\qquad(22) V=U⊕U⊥(22)
(2)正交投影:

定理8:设 U U U是酉空间 V V V的1个子空间,且 V = U ⊕ U ⊥ V=U\oplus U^⊥ V=U⊕U⊥,则对 α ∈ V , α 1 ∈ U α∈V,α_1∈U α∈V,α1∈U是 α α α在 U U U上的正交投影当且仅当 d ( α , α 1 ) ≤ d ( α , γ ) ( ∀ γ ∈ U ) d(α,α_1)≤d(α,γ)\,(∀γ∈U) d(α,α1)≤d(α,γ)(∀γ∈U)
(3)最佳逼近元:

若 U U U为有限维子空间,则由定理7得 V = U ⊕ U ⊥ V=U\oplus U^⊥ V=U⊕U⊥,于是 V V V中任一向量 α α α在 U U U上有正交投影 α 1 = ∑ i = 1 m ( α , η i ) η i α_1=\displaystyle\sum_{i=1}^m(α,η_i)η_i α1=i=1∑m(α,ηi)ηi,其中 η 1 . . . η m η_1...η_m η1...ηm是 U U U的1个标准正交基,从而根据定理8得, V V V中任一向量 α α α在 U U U上的最佳逼近元存在且唯一,它就是 α α α在 U U U上的正交投影 α 1 α_1 α1
二.酉变换与埃尔米特变换(10.5)
1.酉变换
(1)概念:

(2)性质:

命题2:酉空间 V V V上的酉变换一定是线性变换,并且是单射,从而是可逆的
命题4:酉空间 V V V上2个酉变换的乘积还是酉变换,酉变换的逆变换仍是酉变换
定理9:设 Ꭿ Ꭿ Ꭿ是 n n n维酉空间 V V V上的1个酉变换,则 V V V中存在1个标准正交基,使得 Ꭿ Ꭿ Ꭿ在此基下的矩阵是对角矩阵
推论1: n n n级酉矩阵一定酉相似于1个对角矩阵
(3)判定:
命题3:酉空间 V V V上的1个变换 Ꭿ Ꭿ Ꭿ是酉变换当且仅当 Ꭿ Ꭿ Ꭿ是 V V V到自身的1个保距同构
命题5: n n n维酉空间 V V V到自身的1个映射 Ꭿ Ꭿ Ꭿ如果保持向量的内积不变,那么 Ꭿ Ꭿ Ꭿ是酉变换
命题6: n n n维酉空间 V V V上的线性变换 Ꭿ Ꭿ Ꭿ是酉变换
⇔ Ꭿ \,\,\,\,\:\,⇔Ꭿ ⇔Ꭿ把 V V V的标准正交基映成标准正交基
⇔ Ꭿ \,\,\,\,\:\,⇔Ꭿ ⇔Ꭿ在 V V V的标准正交基下的矩阵是酉矩阵
(4)特征值:
命题7: n n n维酉空间 V V V上的酉变换 Ꭿ Ꭿ Ꭿ的特征值的模等于1
即酉变换的特征值均在单位圆上
(5)不变子空间:
命题8:设 Ꭿ Ꭿ Ꭿ是酉空间 V V V上的1个酉变换,若 W W W是 V V V的1个有限维子空间.且 W W W是 Ꭿ Ꭿ Ꭿ的1个不变子空间,则 W ⊥ W^⊥ W⊥也是 Ꭿ Ꭿ Ꭿ的不变子空间
2.埃尔米特变换(Hermite Transformation)
(1)概念:

(2)性质:
命题9:酉空间 V V V上的埃尔米特变换 Ꭿ Ꭿ Ꭿ一定是线性变换
定理10:设 Ꭿ Ꭿ Ꭿ是 n n n维酉空间 V V V上的1个埃尔米特变换,则 V V V中存在1个标准正交基,使得 Ꭿ Ꭿ Ꭿ在此基下的矩阵是实对角矩阵
推论1: n n n级埃尔米特矩阵一定酉相似于1个实对角矩阵
(3)判定:
命题10: n n n维酉空间 V V V上的线性变换 Ꭿ Ꭿ Ꭿ是埃尔米特变换当且仅当 Ꭿ Ꭿ Ꭿ在 V V V的任意1个标准正交基下的矩阵 A A A满足 A ∗ = A ( 27 ) A^*=A\qquad(27) A∗=A(27)满足(27)式的 n n n级复矩阵 A A A称为埃尔米特矩阵(Hermite Matrix)或自伴矩阵
(4)特征值:
命题11:酉空间 V V V上的埃尔米特变换 Ꭿ Ꭿ Ꭿ如果有特征值,那么其特征值是实数
(5)不变子空间:
命题12:设 Ꭿ Ꭿ Ꭿ是酉空间 V V V上的1个埃尔米特变换,若 W W W是 V V V的1个有限维子空间.且 W W W是 Ꭿ Ꭿ Ꭿ的1个不变子空间,则 W ⊥ W^⊥ W⊥也是 Ꭿ Ꭿ Ꭿ的不变子空间
三.线性变换的伴随变换
1.概念:

2.唯一性:
定理11:对于 n n n维复(实)内积空间 V V V上的任一线性变换 Ꭿ Ꭿ Ꭿ,都存在唯一的1个伴随变换 Ꭿ ∗ Ꭿ^* Ꭿ∗
3.矩阵表示:
定理12:设 Ꭿ Ꭿ Ꭿ是 n n n维复(实)内积空间 V V V上的1个线性变换,如果 Ꭿ Ꭿ Ꭿ在 V V V的1个标准正交基 η 1 , η 2 . . . η n η_1,η_2...η_n η1,η2...ηn下的矩阵为 A A A,那么 Ꭿ ∗ Ꭿ^* Ꭿ∗在该标准正交基下的矩阵为 A ∗ A^* A∗
4.性质:
定理13:设 V V V是复(实)内积空间, Ꭿ , B Ꭿ,ℬ Ꭿ,B是 V V V上的线性变换, k ∈ C ( k∈C( k∈C(或 R ) R) R).如果 Ꭿ , B Ꭿ,ℬ Ꭿ,B都有伴随变换,那么 Ꭿ + B , k Ꭿ , Ꭿ B , Ꭿ ∗ Ꭿ+ℬ,kᎯ,Ꭿℬ,Ꭿ^* Ꭿ+B,kᎯ,ᎯB,Ꭿ∗都有伴随变换,且 ( Ꭿ + B ) ∗ = Ꭿ ∗ + B ∗ ( k Ꭿ ) ∗ = k ˉ Ꭿ ∗ ( Ꭿ B ) ∗ = B ∗ Ꭿ ∗ ( Ꭿ ∗ ) ∗ = Ꭿ (Ꭿ+ℬ)^*=Ꭿ^*+ℬ^*\\(kᎯ)^*=\bar{k}Ꭿ^*\\(Ꭿℬ)^*=ℬ^*Ꭿ^*\\(Ꭿ^*)^*=Ꭿ (Ꭿ+B)∗=Ꭿ∗+B∗(kᎯ)∗=kˉᎯ∗(ᎯB)∗=B∗Ꭿ∗(Ꭿ∗)∗=Ꭿ进一步,如果 Ꭿ Ꭿ Ꭿ可逆且 Ꭿ − 1 Ꭿ^{-1} Ꭿ−1也有伴随变换,那么 Ꭿ ∗ Ꭿ^* Ꭿ∗也可逆,且 ( Ꭿ ∗ ) − 1 = ( Ꭿ − 1 ) ∗ (Ꭿ^*)^{-1}=(Ꭿ^{-1})^* (Ꭿ∗)−1=(Ꭿ−1)∗
四.正规变换
1.概念:

2.正规变换与对角矩阵的关系

(1)准备工作:
引理1:设 Ꭿ Ꭿ Ꭿ是复(实)内积空间 V V V上的正规变换,则对 ∀ α ∈ V \forallα∈V ∀α∈V,有 ∣ Ꭿ α ∣ = ∣ Ꭿ ∗ α ∣ ( 45 ) |Ꭿα|=|Ꭿ^*α|\qquad(45) ∣Ꭿα∣=∣Ꭿ∗α∣(45)
引理2:设 Ꭿ Ꭿ Ꭿ是复(实)内积空间 V V V上的正规变换, c ∈ C ( c∈C( c∈C(或 R ) R) R),则 c I − Ꭿ cℐ-Ꭿ cI−Ꭿ也是 V V V上的正规变换
定理14:设 Ꭿ Ꭿ Ꭿ是复(实)内积空间 V V V上的正规变换,则 λ 1 λ_1 λ1是 Ꭿ Ꭿ Ꭿ的1个特征值当且仅当 λ 1 ˉ \bar{λ_1} λ1ˉ是 Ꭿ ∗ Ꭿ^* Ꭿ∗的1个特征值; ξ ξ ξ是 Ꭿ Ꭿ Ꭿ的属于特征值 λ 1 λ_1 λ1的1个特征向量当且仅当是 ξ ξ ξ是 Ꭿ ∗ Ꭿ^* Ꭿ∗的属于特征值 λ 1 ˉ \bar{λ_1} λ1ˉ的1个特征向量
定理15:设 Ꭿ Ꭿ Ꭿ是复(实)内积空间 V V V上的任一线性变换,且 Ꭿ Ꭿ Ꭿ有伴随变换 Ꭿ ∗ Ꭿ^* Ꭿ∗.如果 W W W是 Ꭿ Ꭿ Ꭿ的不变子空间,那么 W ⊥ W^⊥ W⊥是 Ꭿ ∗ Ꭿ^* Ꭿ∗的不变子空间
(2)充分性:
定理16:设 Ꭿ Ꭿ Ꭿ是有限维酉空间 V V V上的正规变换,则 V V V中存在1个标准正交基,使得 Ꭿ Ꭿ Ꭿ在此基下的矩阵是对角矩阵
(3)正规矩阵与对角矩阵的关系:
定理17:对于复数域上的任一 n n n级正规矩阵 A A A,存在1个酉矩阵 P P P,使得 P − 1 A P P^{-1}AP P−1AP为对角矩阵
3.酉矩阵,埃尔米特矩阵与对角矩阵的关系

(2)酉矩阵与对角矩阵的关系:
定理18:任一 n n n级酉矩阵 A A A一定酉相似于1个对角矩阵 d i a g { e i θ 1 , e i θ 2 . . . e i θ n } ( 47 ) diag\,\{e^{iθ_1},e^{iθ_2}...e^{iθ_n}\}\qquad(47) diag{eiθ1,eiθ2...eiθn}(47)其中 0 ≤ θ j ≤ 2 π ( j = 1 , 2... n ) 0≤θ_j≤2\pi\,(j=1,2...n) 0≤θj≤2π(j=1,2...n)
(2)埃尔米特矩阵与对角矩阵的关系:
定理19:任一 n n n级埃尔米特矩阵都酉相似于1个实对角矩阵
五.埃尔米特型
1.埃尔米特型
(1)概念:

(2)性质:
定理20:对于 n n n元埃尔米特型 x ∗ A x x^*Ax x∗Ax,存在酉替换 x = P y ( x=Py( x=Py(即 P P P是酉矩阵 ) ) ),使得 x ∗ A x = λ 1 y 1 y 1 ˉ + λ 2 y 2 y 2 ˉ + . . . + λ n y n y n ˉ ( 55 ) x^*Ax=λ_1y_1\bar{y_1}+λ_2y_2\bar{y_2}+...+λ_ny_n\bar{y_n}\qquad(55) x∗Ax=λ1y1y1ˉ+λ2y2y2ˉ+...+λnynynˉ(55)其中 λ 1 , λ 2 . . . λ n ∈ R λ_1,λ_2...λ_n∈R λ1,λ2...λn∈R是 A A A的全部特征值
2.正定埃尔米特型
(1)概念:

(2)判定:
定理21:设 A A A是 n n n级埃尔米特矩阵,则下列命题等价:
① A ①A ①A是正定埃尔米特矩阵
② ② ②对任意 n n n级可逆复矩阵 B B B,有 B ∗ A B B^*AB B∗AB是正定埃尔米特矩阵
③ A ③A ③A的特征值全部大于0
④ ④ ④存在 n n n级可逆复矩阵 C C C,使得 C ∗ A C = I C^*AC=I C∗AC=I
⑤ A = Q ∗ Q ⑤A=Q^*Q ⑤A=Q∗Q,其中 Q Q Q是 n n n级可逆复矩阵
⑥ A ⑥A ⑥A的所有顺序主子式全部大于0
A A A的所有主子式全部大于0









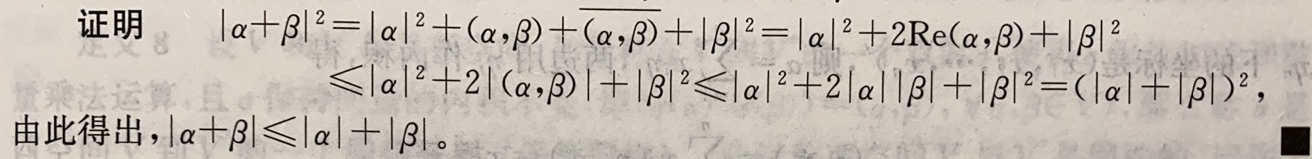
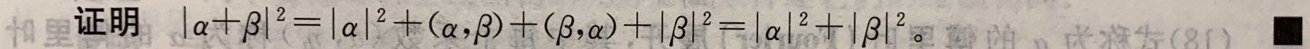

































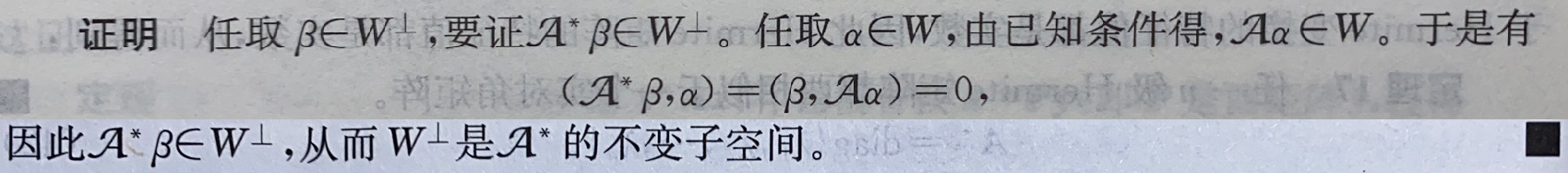





















 1373
1373











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








