【ZED】从零开始使用ZED相机（五）：Opencv+Python实现相机标定（双目）

最新推荐文章于 2025-03-16 12:14:01 发布

摇曳的树

最新推荐文章于 2025-03-16 12:14:01 发布

阅读量7.4k

点赞数 8

文章标签： opencv python 计算机视觉

本文链接：https://blog.csdn.net/qq_44703886/article/details/122987288

版权

引言

同样Opencv+Python实现双目相机的标定，单目标定详见【ZED】从零开始使用ZED相机（五）：Opencv+Python实现相机标定（单目）

1 cv2.stereoCalibrate 函数介绍

调用方法
stereoCalibrate(objectPoints, imagePoints1, imagePoints2, cameraMatrix1, distCoeffs1, cameraMatrix2, distCoeffs2, imageSize, R=None, T=None, E=None, F=None, flags=None, criteria=None)
# 参数含义
objectPoints- vector<point3f> 型的数据结构，存储标定角点在世界坐标系中的位置
imagePoints1- vector<vector<point2f>> 型的数据结构，存储标定角点在第一个摄像机下的投影后的亚像素坐标
imagePoints2- vector<vector<point2f>> 型的数据结构，存储标定角点在第二个摄像机下的投影后的亚像素坐标
cameraMatrix1-输入/输出型的第一个摄像机的相机矩阵。如果CV_CALIB_USE_INTRINSIC_GUESS , CV_CALIB_FIX_ASPECT_RATIO ,CV_CALIB_FIX_INTRINSIC , or CV_CALIB_FIX_FOCAL_LENGTH其中的一个或多个标志被设置，该摄像机矩阵的一些或全部参数需要被初始化
distCoeffs1-第一个摄像机的输入/输出型畸变向量。根据矫正模型的不同，输出向量长度由标志决定
cameraMatrix2-输入/输出型的第二个摄像机的相机矩阵。参数意义同第一个相机矩阵相似
distCoeffs2-第一个摄像机的输入/输出型畸变向量。根据矫正模型的不同，输出向量长度由标志决定
imageSize-图像的大小
R-输出型，第一和第二个摄像机之间的旋转矩阵
T-输出型，第一和第二个摄像机之间的平移矩阵
E-输出型，基本矩阵
F-输出型，基础矩阵
term_crit-迭代优化的终止条件
flag-
 CV_CALIB_FIX_INTRINSIC 如果该标志被设置，那么就会固定输入的cameraMatrix和distCoeffs不变，只求解R,T,E,F
 CV_CALIB_USE_INTRINSIC_GUESS 根据用户提供的cameraMatrix和distCoeffs为初始值开始迭代
 CV_CALIB_FIX_PRINCIPAL_POINT 迭代过程中不会改变主点的位置
 CV_CALIB_FIX_FOCAL_LENGTH 迭代过程中不会改变焦距
 CV_CALIB_SAME_FOCAL_LENGTH 强制保持两个摄像机的焦距相同
 CV_CALIB_ZERO_TANGENT_DIST 切向畸变保持为零
 CV_CALIB_FIX_K1,...,CV_CALIB_FIX_K6 迭代过程中不改变相应的值。如果设置了 CV_CALIB_USE_INTRINSIC_GUESS 将会使用用户提供的初始值，否则设置为零
 CV_CALIB_RATIONAL_MODEL 畸变模型的选择，如果设置了该参数，将会使用更精确的畸变模型，distCoeffs的长度就会变成8

2 cv2.stereoCalibrate 实现双目标定

分别采集左右相机拍摄的棋盘格图象各15-20张左右，分别放在两个文件夹中（笔者采集的比较多，MATLAB计算的重投影误差太大时可以剔除掉一部分图象）：
在这里插入图片描述
实现代码如下：

# 类三：相机标定执行函数(双目校正)
class Stereo_calibrate():  # 执行校正
    def __init__(self):
        # 终止条件
        self.criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
        # 准备对象点，棋盘方块交界点排列：6行8列 如 (0,0,0), (1,0,0), (2,0,0) ....,(6,8,0)
        self.row,self.col = 8,11
        self.objpoints = np.zeros((self.row * self.col, 3), np.float32)
        self.objpoints[:, :2] = np.mgrid[0:self.row, 0:self.col].T.reshape(-1, 2)

    def exe(self,dir_l,dir_r):
        objectpoints = [] # 真实世界中的3d点
        imgpoints_l = []
        imgpoints_r = []
        # 标定所用图像
        images_l = glob.glob('%s/*'%dir_l)
        images_r = glob.glob('%s/*' % dir_r)
        for i in range(len(images_l)):
            img_l = cv2.imread(images_l[i])
            gray_l = cv2.cvtColor(img_l, cv2.COLOR_BGR2GRAY)
            img_r = cv2.imread(images_r[i])
            gray_r = cv2.cvtColor(img_r, cv2.COLOR_BGR2GRAY)
            # 寻找到棋盘角点
            ret1, corners_l = cv2.findChessboardCorners(img_l, (self.row, self.col), None)
            ret2, corners_r = cv2.findChessboardCorners(img_r, (self.row, self.col), None)
            # 如果找到，添加对象点，图像点（细化之后）
            if ret1 == True and ret2 == True:
                # 添加每幅图的对应3D-2D坐标
                objectpoints.append(self.objpoints)
                corners_l = cv2.cornerSubPix(gray_l, corners_l, (11, 11), (-1, -1),self.criteria)
                imgpoints_l.append(corners_l)
                corners_r = cv2.cornerSubPix(gray_r, corners_r, (11, 11), (-1, -1), self.criteria)
                imgpoints_r.append(corners_r)
        #         # 绘制并显示拐角
        #         cv2.drawChessboardCorners(img_l, (self.row, self.col), corners_l, ret)
        #         cv2.drawChessboardCorners(img_r, (self.row, self.col), corners_r, ret)
        #         view  = np.concatenate((img_l, img_r), axis=1)
        #         cv2.namedWindow('View')
        #         cv2.imshow("View", cv2.resize(view,(1920,540)))
        #         cv2.waitKey(0)
        # cv2.destroyAllWindows()
        # 利用单目校正函数实现相机内参初始化
        ret, m1, d1, _, _ = cv2.calibrateCamera(objectpoints, imgpoints_l, gray_l.shape[::-1], None, None)
        ret, m2, d2, _, _= cv2.calibrateCamera(objectpoints, imgpoints_l, gray_l.shape[::-1], None, None)
        # config
        flags = 0
        # flags |= cv2.CALIB_FIX_ASPECT_RATIO
        flags |= cv2.CALIB_USE_INTRINSIC_GUESS
        # flags |= cv2.CALIB_SAME_FOCAL_LENGTH
        # flags |= cv2.CALIB_ZERO_TANGENT_DIST
        flags |= cv2.CALIB_RATIONAL_MODEL
        # flags |= cv2.CALIB_FIX_K1
        # flags |= cv2.CALIB_FIX_K2
        # flags |= cv2.CALIB_FIX_K3
        # flags |= cv2.CALIB_FIX_K4
        # flags |= cv2.CALIB_FIX_K5
        # flags |= cv2.CALIB_FIX_K6
        stereocalib_criteria = (cv2.TERM_CRITERIA_COUNT +
                                cv2.TERM_CRITERIA_EPS, 100, 1e-5)
        # 输入参数：真实3d坐标点，左相机像素点、右相机像素点、左内参、左畸变、右内参、右畸变、图像尺寸、一些配置
        # 输出值：未知、左内参、左畸变、右内参、右畸变（迭代优化后的）、旋转矩阵、平移向量、本质矩阵、基础矩阵
        ret, m1, d1,m2, d2, R, t, E, F = cv2.stereoCalibrate(objectpoints,imgpoints_l,imgpoints_r,
                                                                       m1, d1,m2, d2, gray_l.shape[::-1],
                                                                       criteria=stereocalib_criteria, flags=flags)
        # 构建单应性矩阵
        plane_depth = 40000000.0  # arbitrary plane depth
        # TODO: Need to understand effect of plane_depth. Why does this improve some boards' cals?
        n = np.array([[0.0], [0.0], [-1.0]])
        d_inv = 1.0 / plane_depth
        H = (R - d_inv * np.dot(t, n.transpose()))
        H = np.dot(m2, np.dot(H, np.linalg.inv(m1)))
        H /= H[2, 2]
        # rectify Homography for right camera
        disparity = (m1[0, 0] * t[0] / plane_depth)
        H[0, 2] -= disparity
        H = H.astype(np.float32)
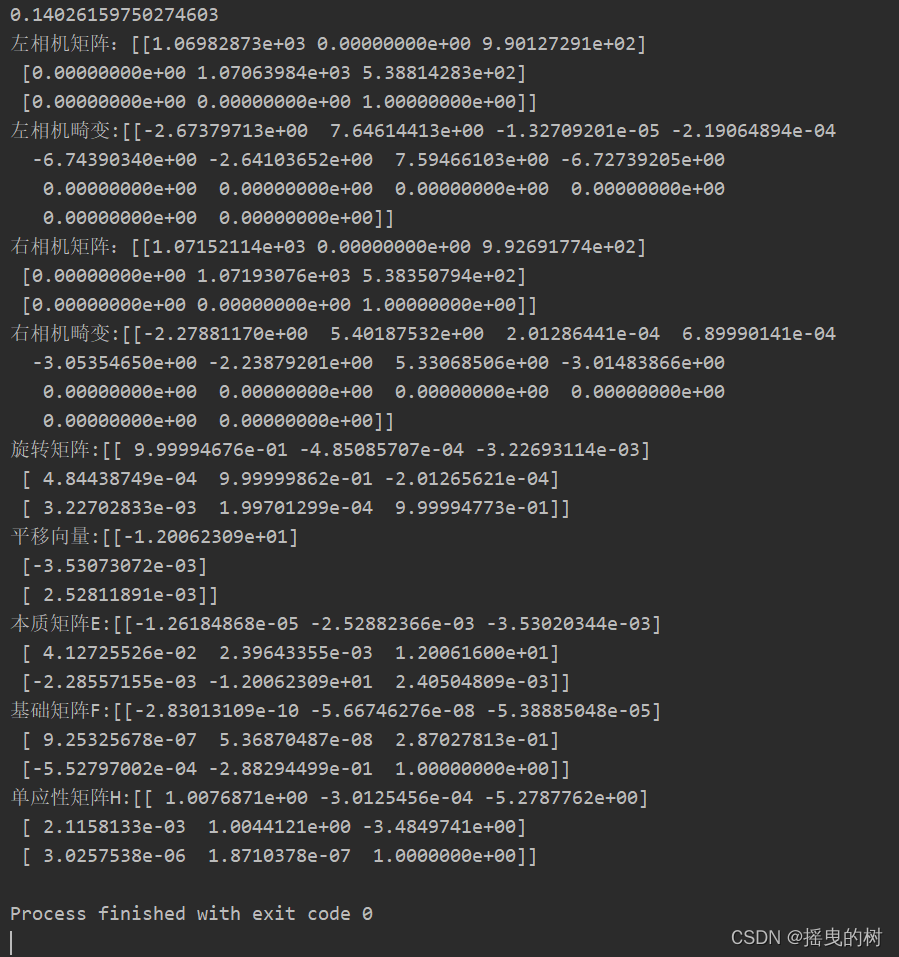
        print(ret,'\n左相机矩阵：%s\n左相机畸变:%s\n右相机矩阵：%s\n右相机畸变:%s\n旋转矩阵:%s\n平移向量:%s'
                  '\n本质矩阵E:%s\n基础矩阵F:%s\n单应性矩阵H:%s'
              %(m1, d1,m2, d2, R, t, E, F,H))

函数调用如下：

if __name__ == "__main__":
    # 双目校正
    cal = Stereo_calibrate()
    cal.exe(r'E:\Alian\yolov5\zed-examples-master\images\1080\L',r'E:\Alian\yolov5\zed-examples-master\images\1080\R')