- 什么是泰勒公式?
- 简单来讲就是用一个多项式函数去逼近一个给定的函数(即尽量使多项式函数图像拟合给定的函数图像),注意,逼近的时候一定是从函数图像上的某个点展开。如果一个非常复杂的函数,想求其某点的值,直接求无法实现,这时候可以使用泰勒公式去近似的求该值,这是泰勒公式的应用之一。泰勒公式在机器学习中主要应用于梯度迭代。
- 为什么使用多项式逼近?
- 多项式
是最简单的一类初等函数。关于多项式,由于它本身的运算仅是有限项加减法和乘法,所以在数值计算方面,多项式是人们乐于使用的工具。因此我们经常用多项式来近似表达函数。这也是为什么泰勒公式选择多项式函数去近似表达给定的函数。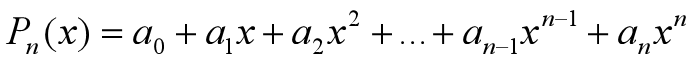
- 多项式
-
泰勒公式的推导

泰勒公式的推导
最新推荐文章于 2025-04-30 09:36:22 发布























 1790
1790

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








