欧式距离(Euclidean Distance,ED)算法,是利用测序数据寻找混池间存在显著差异标记,并以此评估与性状关联区域的方法。理论上,BSA项目构建的两个混池间除了目标性状相关位点存在差异,其他位点均趋向于一致,因此非目标位点的ED值应趋向于0。ED值越大表明该标记在两混池间的差异越大。
ED算法不依赖于亲本的数据,也可以做F1子代的QTL定位,所以这种方式适用的群体类型是比较多的。
在本次脚本里,利用了两混池间基因型存在差异的SNP位点,统计各个碱基在不同混池中的深度,并计算每个位点ED值,为消除背景噪音,对原始ED值进行乘方处理,本项目取原始ED的5次方作为关联值以达到消除背景噪音的功能,然后采用SNPNUM方法对ED值进行拟合。
一、使用到的数据
本次分析我还使用和帖子重测序BSA--SNP-index方法关联分析 (qq.com)一样的数据(all.clean.snp.qtlseq.vcf.gz文件,解压一下),但是不用它的亲本数据,只用到两个子代极端混池的数据。对比一下两种结果的数据。
再看一下这个文件,使用本次脚本不需要事先把其它不需要的数据过滤(比如亲本列数据去除),因为只要给脚本指定要处理的两个混池的名字,它就会去读取两个混池的数据,,用于后续分析

二、在linux中运行
下面是在linux下具体运行BSA_ED.py步骤

可以看一下脚本里有的参数,可以根据需要设置

运行命令
python ~/software/dai_scripts/BSA_ED.py -vcf all.clean.snp.qtlseq.vcf -bulk1 S-pool -bulk2 T-pool -power 5 -minDP 4 -maxDP 100 -outpre all.clean.snp.BSA-ED下面是BSA_ED.py脚本的全部内容
import argparse # 导入解析命令行参数的模块
from collections import defaultdict # 导入collections模块中的defaultdict,用于创建默认字典
import math # 导入用于数学计算的模块
from statistics import mean # 导入statistics模块中的mean函数,用于计算平均值
def parse_vcf_header(vcf_file):
col1 = 0 # 初始化bulk1的列索引
col2 = 0 # 初始化bulk2的列索引
for line in vcf_file:
if line.startswith("#CHROM"):
header = line.strip().split("\t") # 分割表头行以获取列名
col1 = header.index(args.bulk1) # 获取bulk1的列索引
col2 = header.index(args.bulk2) # 获取bulk2的列索引
return col1, col2
return col1, col2 # 如果找不到表头,返回默认的列索引
# 自定义一个函数,计算ED值和ED的幂次方
def calculate_edpower(ad1, ad2, power):
dp1 = sum(ad1) # 计算bulk1的总深度
dp2 = sum(ad2) # 计算bulk2的总深度
# 根据最小和最大深度进行过滤
if dp1 == 0 or dp2 == 0 or dp1 < args.minDP or dp1 > args.maxDP or dp2 < args.minDP or dp2 > args.maxDP:
return None # 如果不符合深度要求,返回None
# 计算等位基因频率
freq1 = [ad / dp1 for ad in ad1] # 创建一个新的列表 freq1,其中的每个元素都是通过将列表 ad1 中的元素 ad 除以 dp1 得到的结果
freq2 = [ad / dp2 for ad in ad2]
# 计算平方差和ED
sqr_diff = [(freq1[i] - freq2[i]) ** 2 for i in range(len(ad1))] # 用于计算两个列表 freq1 和 freq2 中相同索引位置上元素的平方差,然后将结果存储在一个名为 sqr_diff 的新列表中
ed = math.sqrt(sum(sqr_diff)) # 用于计算一个名为 ed 的变量,它代表了一个数值列表 sqr_diff 中所有元素的平方和的平方根(即欧几里德距离的计算)
# 计算ED的幂次方
ed_power = ed ** power
return ed_power
def main():
# 输入文件是vcf,获得.snp_EDpower{args.power}.tsv文件
with open(args.vcf, 'r') as vcf_file, open(args.outpre + f".snp_EDpower{args.power}.tsv", 'w') as snp_output:
col1, col2 = parse_vcf_header(vcf_file) # 解析VCF文件的表头,并获取bulk1和bulk2的列索引
snp_output.write("CHROM\tPOS\t{0}_AD\t{1}_AD\tED{2}\n".format(args.bulk1, args.bulk2, args.power)) # 写入输出文件的表头
print(args.bulk1 + ": " + str(col1) + " " + args.bulk2 + ": " + str(col2)) # 在屏幕上打印出两个子代极端数据在vcf哪些列
ed_dict = defaultdict(dict) # 创建一个用于存储ED值的字典
for line in vcf_file:
if line.startswith("#"):
continue # 跳过注释行
fields = line.strip().split("\t") # 分割行数据
ad_field = fields[8].split(":").index("AD") # 获取AD字段的索引
ad1 = [int(ad) for ad in fields[col1].split(":")[ad_field].split(",")] # 解析bulk1的AD信息
ad2 = [int(ad) for ad in fields[col2].split(":")[ad_field].split(",")] # 解析bulk2的AD信息
ed_power = calculate_edpower(ad1, ad2, args.power) # 计算ED幂次方
if ad1.count(0) == 1 and ad2.count(0) == 1 and ed_power == 0:
continue # 如果在某一点,两个子代极端混池纯和且基因型一致,ED幂次方为零,则跳过
if ed_power is not None: # 由上面知ed_power值为None的是不符合深度要求,这里我们的条件设置要挑选符合要求的
ed_dict[fields[0]][fields[1]] = ed_power # 存储ED幂次方值到字典中
snp_output.write(f"{fields[0]}\t{fields[1]}\t{','.join(map(str, ad1))}\t{','.join(map(str, ad2))}\t{ed_power}\n") # 写入数据到输出文件
# 输入文件是.snp_EDpower{args.power}.tsv,获得拟合的数据
with open(args.outpre + f".sliding_EDpower{args.power}.tsv", 'w') as sliding_output:
sliding_output.write("CHROM\tPOS\tSTART\tEND\tnSNP\tmean_ED{0}\n".format(args.power)) # 写入输出文件的表头
for chrom, pos_dict in ed_dict.items():
pos_list = sorted(pos_dict.keys()) # 获取按位置排序的ED字典的键列表
max_pos = max(int(pos) for pos in pos_list) # 获取每条染色体的最长长度
window = args.window # 窗口大小
step = args.step # 步长
window = window * 1000 # 将窗口大小转换为千字节
step = step * 1000 # 将步长转换为千字节
if int(max_pos) <= window:
mean_ed = mean(ed_dict[chrom][pos] for pos in pos_list)
sliding_output.write(f"{chrom}\t{int(max_pos) / 2}\t1\t{max_pos}\t{len(pos_list)}\t{mean_ed}\n") # 如果最大位置小于窗口大小,计算平均ED并写入输出文件
else:
win_edges = list(range(window, int(max_pos) + 1, step)) # 生成窗口边界列表
for edge in win_edges:
start = edge - window + 1
sub_pos = [pos for pos in pos_list if start <= int(pos) < edge] # 根据窗口边界筛选位置
if sub_pos:
mean_ed = mean(ed_dict[chrom][pos] for pos in sub_pos) # 计算子窗口中的平均ED
else:
mean_ed = "nan"
mean_pos = edge - window / 2
sliding_output.write(f"{chrom}\t{int(mean_pos):d}\t{start}\t{edge}\t{len(sub_pos)}\t{mean_ed}\n") # 写入子窗口的数据到输出文件
if __name__ == "__main__":
parser = argparse.ArgumentParser(description="从VCF文件计算ED幂次方")
parser.add_argument('-vcf', required=True, help='输入的VCF文件')
parser.add_argument('-bulk1', required=True, help='bulk1的样本名称')
parser.add_argument('-bulk2', required=True, help='bulk2的样本名称')
parser.add_argument('-power', type=int, default=5, help='ED幂次方(默认为5)')
parser.add_argument('-minDP', type=int, default=4, help='变异的最小深度(每个样本)(默认为4)')
parser.add_argument('-maxDP', type=int, default=250, help='变异的最大深度(每个样本)(默认为250)')
parser.add_argument('-window', type=int, default=2000, help='窗口大小(千字节)(默认为2000)')
parser.add_argument('-step', type=int, default=100, help='步长(千字节)(默认为100)')
parser.add_argument('-outpre', required=True, help='输出文件前缀')
args = parser.parse_args() # 解析命令行参数
main() # 调用主函数执行脚本逻辑把all.clean.snp.BSA-ED.snp_EDpower5.tsv复制到excel中看一下
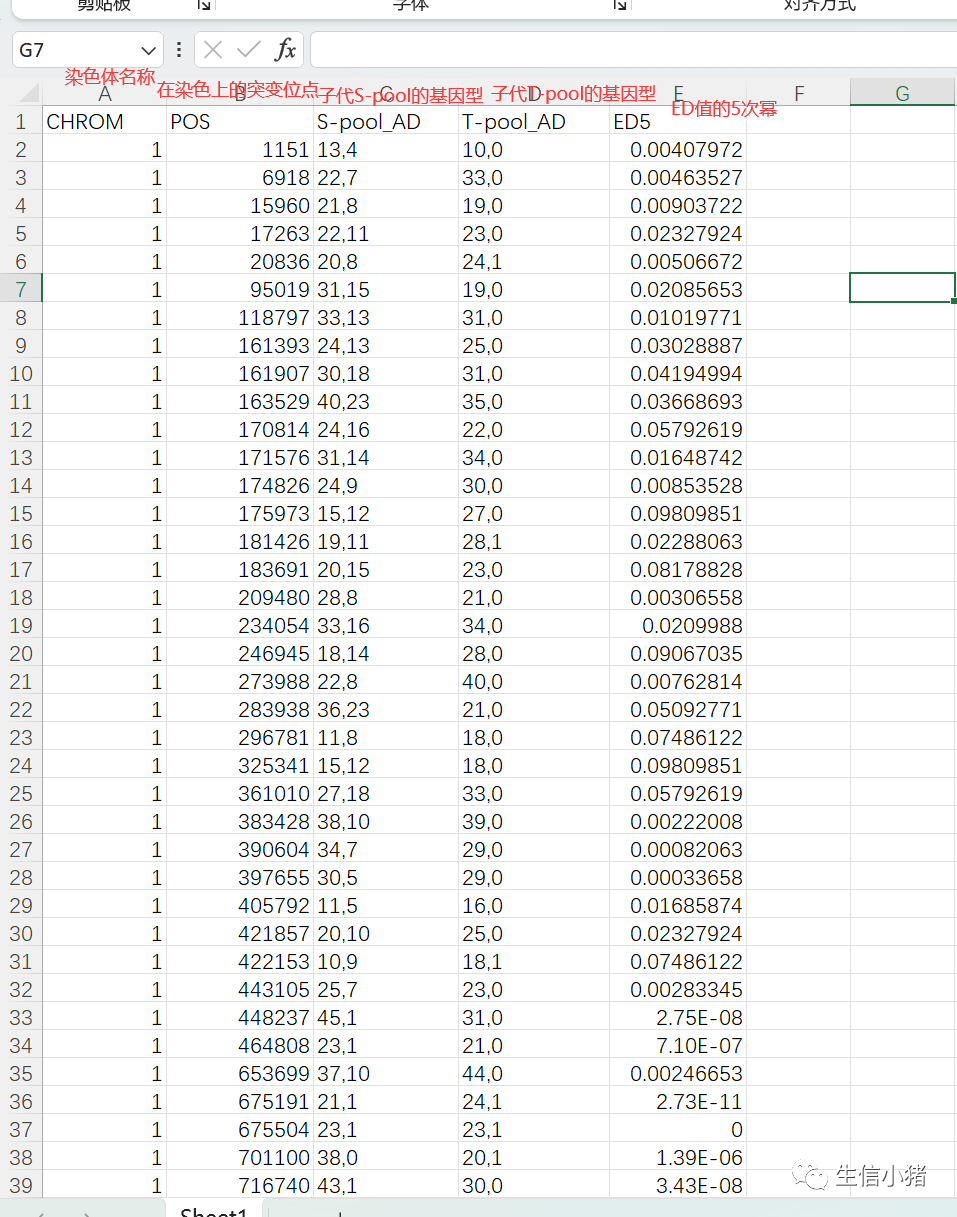
ED5值是怎么得到的?
这里拿1号染色体上的1151位点来演示

为什么说ED值越大表明该标记在两混池间的差异越大?
还以1151位点举例,从ED的计算公式可知,如果ref_a的值达到最大,这里最大可以达到17,那么alt_a就为0,该位点的基因型就是纯和的且和参考基因组一致;这时如果ref_b的值达到最小为0,那么alt_b的值达到最大10,该位点的基因型就是纯和的且和参考基因组完全不一致。
这时相当于子代S-pool和S-pool的基因型纯和且不一致,该标记在两混池间的差异越大,ed值也达到了最大。
把all.clean.snp.BSA-ED.sliding_EDpower5.tsv复制到excel中看一下

第5列nSNP:是在2M的区域内包含的snp突变位点个数,
第6列mean_ED5:这列是利用all.clean.snp.BSA-ED.snp_EDpower5.tsv数据计算来的

中间还有很多数据

至于滑窗和步长的理解可以参考重测序BSA--SNP-index方法关联分析 (qq.com)这个帖子sliding_window.tsv 文件是怎么计算得到的,原理上是一样的。
三、补充
其实在脚本计算ED值之前,脚本对数据进行了两个过滤
第1个过滤:过滤掉不符合深度要求的,默认是保留深度大于4小于250的数据,也可以根据需要调整参数-minDP和-maxDP。这里我为了和我之前的重测序BSA--SNP-index方法关联分析 (qq.com)分析保持一致,设置了-minDP 4 -maxDP 100参数。

第2个过滤:过滤掉两个子代极端混池纯和且基因型一致的数据

也就是比如说把下面这部分数据过滤掉

这部分数据的两个子代极端混池纯和且基因型一致,那么按照ED值计算公式,ED就会为0。这也就是说为什么非目标位点的ED值应趋向于0。
用这个脚本同样也可以处理indel的变异数据,使用方法和上面一样。























 8370
8370

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








