相机矩阵的分解

你一直在研究一个新的计算机视觉库，并且设法校准了你的相机……现在你要用它做什么？

如果你能找到相机的位置或找出它的视野，那会更有用。你打开了你信赖的 Hartley 和 Zisserman 的副本，它告诉你如何将你的相机分解为内参和外参矩阵 --- 太棒了！

但是当你查看结果时，有些事情不太对劲。也许你的旋转矩阵有一个行列式 -1，导致你的矩阵到四元数函数出错。也许你的焦距是负的，而你不明白为什么。也许你的平移向量错误地声称世界原点在相机后面。或者最糟糕的是，一切看起来都很好，但是当你将它插入 OpenGL 时，你什么都看不到。

今天，我们将介绍将相机矩阵分解为内参矩阵和外参矩阵的过程，并尝试解决可能因不同坐标约定而出现的问题。在后面的文章中，我们将更详细地研究内在矩阵和外在矩阵，我将介绍如何将它们转换为 OpenGL 可用的形式。

NSDT工具推荐： Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割 

1、获取相机矩阵

我假设你已经事先获得了相机矩阵，但如果需要相机校准方面的帮助，我建议你查看 Matlab 的相机校准工具箱。OpenCV 似乎也有一些有用的例程，可以从一系列棋盘图像中自动校准相机，尽管我个人没有使用过它们。像往常一样，Hartley 和 Zisserman 对该主题进行了很好的处理。

2、相机矩阵分解

首先，我们假设你的相机矩阵为 3x4，它将齐次 3D 世界坐标转换为齐次 2D 图像坐标。按照 Hartley 和 Zisserman 的说法，我们将矩阵表示为 P，有时使用块形式会很有用：

其中 M 是可逆的 3x3 矩阵，C 是列向量，表示相机在世界坐标中的位置。一些校准软件提供了 4x4 矩阵，它增加了一行来保存 z 坐标。在这种情况下，只需删除第三行即可获得 3x4 矩阵。

相机矩阵本身可用于将 3D 点投影到 2D，但它有几个缺点：

• 它不会告诉你相机的姿态。
• 它不会告诉你相机的内部几何形状。
• 镜面照明是不可能的，因为你无法在相机坐标中获得表面法线。

为了解决这些缺点，相机矩阵可以分解为两个矩阵的乘积：一个内参矩阵 K 和一个外参矩阵 [R|−RC]

矩阵 K 是一个 3x3 上三角矩阵，用于描述相机的内部参数，例如焦距。R 是一个 3x3 旋转矩阵，其列是相机参考系中世界轴的方向。向量 C 是世界坐标中的相机中心；向量 t = -RC 给出相机坐标中世界原点的位置。我们将在后续文章中更详细地研究这些矩阵中的每一个，今天我们只讨论如何从 P 中获取它们。

恢复相机中心 C 很简单。请注意，P 的最后一列是 -MC，因此只需将其左乘以 −M^−1。

3、在进行 RQ 之前...

为了恢复 R 和 K，我们注意到 R 是正交的，因为它是旋转矩阵，而 K 是上三角矩阵。任何满秩矩阵都可以通过使用 RQ 分解为上三角矩阵和正交矩阵的乘积。

不幸的是，包括 Matlab 在内的许多库都不提供 RQ 分解，但幸运的是，它的朋友 QR 分解通常可用。Solem 的视觉博客有一篇很好的文章，使用一些矩阵翻转实现了缺失的函数；这是一个 Matlab 版本（感谢 Solem 允许我转发这篇文章！）：

function [R Q] = rq(M)
    [Q,R] = qr(flipud(M)')
    R = flipud(R');
    R = fliplr(R);

    Q = Q';   
    Q = flipud(Q);

简单！

4、我看到了双重……四次分解！

只有一个问题：RQ 分解的结果不是唯一的。要看到这一点，请尝试否定 K 的任何列和 R 的相应行：得到的相机矩阵保持不变。大多数人只是强制 K 的对角线元素为正，如果两个条件成立，这是正确的方法：

• 图像的 X/Y 轴指向与相机的 X/Y 轴相同的方向。
• 相机朝正 z 方向看。

Solem 的博客用三行代码优雅地为我们提供了正对角线条目：

# make diagonal of K positive
T = diag(sign(diag(K)));

K = K * T;
R = T * R; # (T is its own inverse)

实际上，相机轴和图像轴不会一致，并且 K 的对角线元素不应为正。强制它们为正可能会导致严重的副作用，包括：

• 物体出现在相机的错误一侧。
• 旋转矩阵的行列式为 -1 而不是 1。
• 不正确的镜面照明。
• 由于 w 坐标为负，可见几何图形不会渲染。

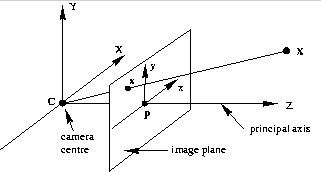
Hartley 和 Zisserman 的坐标约定。请注意，从相机的 POV 观看时，相机和图像 x 轴指向左侧。

在这种情况下，你需要进行一些修复。

首先确保你的相机和世界坐标都具有相同的惯用手性。然后记下校准相机时使用的轴约定。图像 y 轴指向哪个方向，向上还是向下？x 轴？现在考虑相机的坐标轴。你的相机是否朝负 z 轴（OpenGL 风格）俯视？朝正 z 轴（如 Hartley 和 Zisserman）？x 轴指向左还是右？y 轴呢？好的，好的，你明白了。

从全正对角线开始，遵循以下四个步骤：

• 如果图像 x 轴和相机 x 轴指向相反方向，则对 K 的第一列和 R 的第一行取反。
• 如果图像 y 轴和相机 y 轴指向相反方向，则对 K 的第二列和 R 的第二行取反。
• 如果相机朝负 z 轴俯视，则对 K 的第三列取反。保持 R 不变。编辑：也对 R 的第三列取反。
• 如果 R 的行列式为 -1，则对其取反。

请注意，这些步骤中的每一步都使组合相机矩阵保持不变。最后一步相当于将整个相机矩阵 P 乘以 -1。由于 P 是在齐次坐标上操作的，因此将其乘以任何常数都没有效果。

关于步骤 3，Hartley 和 Zisserman 的相机向下看正 z 方向，但在某些现实世界系统（例如 OpenGL）中，相机向下看负 z 轴。这允许 x 和 y 轴指向右上方，从而产生一个感觉自然但仍然是右手坐标系的坐标系。上面的步骤 3 通过在 z 为负时使 w 为正来纠正这个问题。

你可能会对 K3,3为负的事实感到犹豫，但 OpenGL 需要这样做才能正确剪辑。我们将在以后的文章中进一步讨论 OpenGL。

您可以通过检查向量 t=−RC 来仔细检查结果，它是相机坐标中世界原点的位置。如果一切正确，tx,ty,tz 的符号应该反映世界原点在相机中的位置（分别是中心的左/右、中心的上方/下方、相机的前面/后面）。

5、谁翻转了我的轴？

到目前为止，我们对 2D 坐标约定的讨论都涉及校准期间使用的坐标。如果你的应用程序使用不同的 2D 坐标约定，则需要使用 2D 平移和反射来转换 K。

例如，考虑一个相机矩阵，其校准原点在左上角，y 轴向下，但您更喜欢原点在左下角，y 轴向上。要转换，你首先要对图像 y 坐标取反，然后向上平移图像高度 h。得到的固有矩阵 K' 由以下公式给出：

6、结束语

无论你使用哪种坐标约定，上述过程都应为你提供正确的相机分解。我在自己的研究中已在少数场景中对其进行了测试，到目前为止效果良好。

在下一篇文章中，我们将通过交互式演示更详细地研究外部矩阵。

---

原文链接：相机矩阵的分解 - BimAnt