结构光系统标定（四）基于双目视觉的结构光系统标定

最新推荐文章于 2024-11-04 10:37:11 发布

明天的阵雨

最新推荐文章于 2024-11-04 10:37:11 发布

阅读量1.2w

点赞数 35

分类专栏：结构光三维重建结构光系统标定

本文链接：https://blog.csdn.net/u010430651/article/details/104868734

版权

上一篇文章讲了基于多项式拟合的结构光系统标定，实际上就是将一系列待测的长度值，隐式地表达在一个多项式里面，通过拟合的方式去求出从相位计算三维坐标所需的参数。当然，这个名字是我自己取的，不一定准确。

这篇文章会再讲一种标定方法，基于双目视觉的结构光系统标定，这个方法应该更经典，被采用得更多，Google学术搜出来被引量610。当然，这也是我给它取的名字，不正确的话也请指正。

基于双目视觉的结构光系统标定

该方法将投影仪看作是一个摄像机，将结构光系统看作是两个摄像机的双目系统，通过双目视觉标定求摄像机和投影仪的相关参数，正是因此，我给它的名字是基于双目视觉的结构光系统标定。该方法的核心在于让投影仪能像摄像机一样获取图像，实际上是通过PMP方法，找到摄像机的图像和投影仪的图像之间的转换关系，利用摄像机为投影仪拍照，并转换成投影仪获取的图像。

以下原理，和摄像机小孔成像模型、张正友相机标定相关的，我还是不会细讲，而是直接采用，有需要自行补习哦~

结构光系统模型

这个系统模型与上一篇文章中的方法一样，对摄像机和投影仪的摆放位置都没有严格的要求。以下两个系统结构图，第一个是论文里的截图，第二个是我写毕业论文的时候重新画的，原理都一样，你们看哪个顺眼就对着那个分析即可。

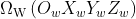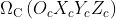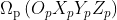${{\Omega }_{\text{W}}}\left( {{O}_{w}}{{X}_{w}}{{Y}_{w}}{{Z}_{w}} \right)$ 、 ${{\Omega }_{\text{C}}}\left( {{O}_{c}}{{X}_{c}}{{Y}_{c}}{{Z}_{c}} \right)$ 、 ${{\Omega }_{\text{p}}}\left( {{O}_{p}}{{X}_{p}}{{Y}_{p}}{{Z}_{p}} \right)$ 分别表示世界坐标系、摄像机坐标系和投影仪坐标系。由于这个系统把投影仪看作摄像机，所以 ${{o}_{c}}{{u}_{c}}{{v}_{c}}$ 、 ${{o}_{p}}{{u}_{p}}{{v}_{p}}$ 分别表示摄像机成像面坐标系和投影仪成像平面坐标系。对于被测物体上一点，其在世界坐标系、摄像机坐标系和投影仪坐标系上的坐标分别为 $\left( {{X}_{w}},{{Y}_{w}},{{Z}_{w}} \right)$ 、 $\left( {{X}_{c}},{{Y}_{c}},{{Z}_{c}} \right)$ 和 $\left( {{X}_{p}},{{Y}_{p}},{{Z}_{p}} \right)$ ，成像在摄像机成像面上的点 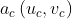${{a}_{c}}\left( {{u}_{c}},{{v}_{c}} \right)$ 和投影仪成像面上的点 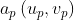${{a}_{p}}\left( {{u}_{p}},{{v}_{p}} \right)$ 上。

世界坐标系、摄像机坐标系、摄像机成像面坐标系之间的转换关系可用下面小孔成像模型的式子来表示

$\left[ \begin{matrix} {{X}_{c}} \\ {{Y}_{c}} \\ {{Z}_{c}} \\ \end{matrix} \right]=\left[ \begin{matrix} {{R}_{c}} & {{t}_{c}} \\ \end{matrix} \right]\left[ \begin{matrix} {{X}_{w}} \\ {{Y}_{w}} \\ {{Z}_{w}} \\ 1 \\ \end{matrix} \right]$

${{s}_{c}}\left[ \begin{matrix} {{u}_{c}} \\ {{v}_{c}} \\ 1 \\ \end{matrix} \right]=\left[ \begin{matrix} {{f}_{cx}} & 0 & {{c}_{cx}} \\ 0 & {{f}_{cy}} & {{c}_{cy}} \\ 0 & 0 & 1 \\ \end{matrix} \right]\left[ \begin{matrix} {{X}_{c}} \\ {{Y}_{c}} \\ {{Z}_{c}} \\ \end{matrix} \right]$ 把两个式子联立可以表示为
${{s}_{c}}\left[ \begin{matrix} {{u}_{c}} \\ {{v}_{c}} \\ 1 \\ \end{matrix} \right]={{H}_{c}}\left[ \begin{matrix} {{X}_{w}} \\ {{Y}_{w}} \\ {{Z}_{w}} \\ 1 \\ \end{matrix} \right]$
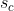其中， ${{s}_{c}}$ 为尺度因子，单应性矩阵

最低0.47元/天解锁文章