如何看待DNA双螺旋结构被发现的过程？

 

DNA作为遗传信息的载体储存着生物的遗传密码，今天我们对DNA的双螺旋结构已经了如指掌。但在探索揭示这一结构的过程中有一些令人深思的故事。

早在20世纪50年代美国生化学家查盖夫（E.Chargaff）不迷信前人的结果，敢于质疑，并利用层析和紫外吸收光谱法对不同生物DNA的碱基组成进行了精确的定量测定，推翻了前人的四核苷酸假说，从而得出重要的结论，总结出以下规律：DNA的组成成分中，腺嘌呤和胸腺嘧啶的摩尔数相等，即A=T；鸟嘌呤和胞嘧啶的摩尔数相等，即G=C；不同生物种属的DNA碱基组成不同；同一个体不同器官不同组织的碱基组成相同。此规律称之为Chargaff 规则。这是碱基配对的重要证据，但遗憾的是他没有给出合理的解释。

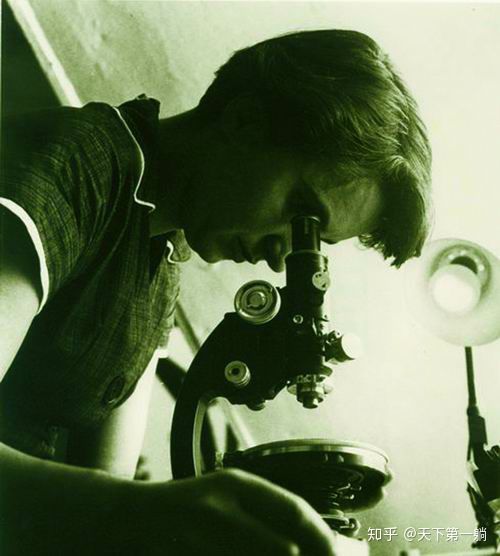
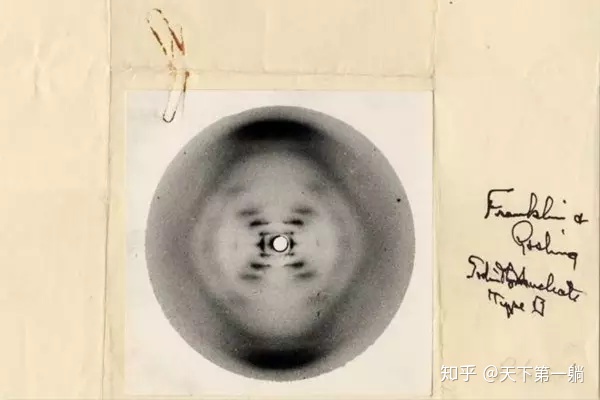
英国物理化学家与晶体学家富兰克林（R.Franklin）和维尔金森（M.Wilkins）两位科学家在DNA的晶体X射线衍射方面作出了卓越贡献，特别是富兰克林在1951年11所得到的高质量的DNA分子X线衍射图是双螺旋模型的重要证据。但是同样遗憾的是她没有首先发表自己的数据，作为DNA化学结构的第一发现者，富兰克林的论文却只能作为DNA双螺旋的一个补充证据，从而与诺贝尔奖擦肩而过。后来克里克在一篇纪念DNA结构发现40周年的文章中说道：“富兰克林的贡献没有受到足够的肯定，她清楚地阐明两种型态的DNA，并且定出A型DNA的密度、大小与对称性。”

20世纪50年代沃森（J.Watson）和克里克（F.Crick）两位年轻人是在查盖夫和富兰克林等人工作的基础上为揭示DNA空间结构的奥秘开始了密切合作。克里克与沃森认为：当时的X射线晶体衍射技术水平尚不足以清晰显示生物大分子较为复杂的三维图像，仅靠数学计算难以确定大分子中所有原子的准确位置。如果设想DNA分子呈螺旋状，则可以依据X射线衍射图上的几组数据，先构建出分子模型的基本形态，再不断调整其中原子排列的位置细节，直到其与真实分子的衍射图十分接近为止。此时得到的即应是DNA的实际立体结构模式。经过了两年来缜密的思考和严密的推断，最终两人在提出了DNA 的二级结构—双螺旋模型，于1953年4月25日发表于《Nature》杂志。这一发现揭示了生物遗传性状得以世代相传的分子机制，它不仅解释了当时已知的DNA理论性质，还将DNA的功能与结构联系起来，奠定了现代生命的科学基础，从而开创了分子生物学的时代。J.Watson、F.Crick和M.Wilkins因此分享了1962年的诺贝尔生理学/医学奖。