1、简介
骨骼蒙皮动画,简称骨骼动画,因其占用磁盘空间少并且动画效果好被广泛用于3D游戏中,它把网格顶点(皮)绑定到一个骨骼层次上面,当骨骼层次变化之后,可以根据绑定信息计算出新的网格顶点坐标,进而驱动该网格变形;一个完整的骨骼动画一般由骨架层次、绑定网格以及一系列关键帧组成,一个关键帧对应于骨架的一个新状态,两个关键帧之间的状态可以通过插值得到;下面介绍骨骼蒙皮动画在SPE中的实现细节,包括骨骼层次的表示、动画数据(关键帧)的组织、关键帧之间的插值方法、软件蒙皮以及硬件蒙皮的实现。
2、骨骼层次的表示
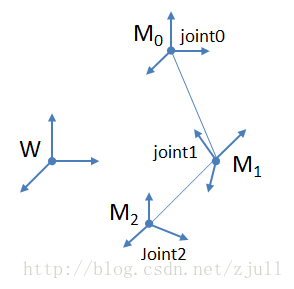
图1:骨骼层次
一个骨骼层次由一系列离散的关节(joint)构成,它们通过父子关系联系在一起,如图1所示;为了方便建模,每个关节的方位信息(位置和朝向)是在它的父空间中定义的,每个关节自身也定义了一个子空间;那怎么表示一个空间呢?一个joint定义的空间可以由该joint在父空间中的位置和朝向确定,位置可以由一个三维向量表示,朝向用一个3x3的矩阵表示,这样一个空间可以用一个3x4的矩阵表示,其中左边3x3部分表示朝向,第4列表示位置,为了后面表示和计算方便,在矩阵中添加一行(0,0,0,1),形成4x4矩阵。如上图所示,Mi表示了各个joint的空间矩阵,M2定义在它的父空间M1中,M1定义在M0中,M0所在的关节joint0叫根关节,因为它直接定义在建模坐标系空间W中,W是个单位矩阵,另外,一个骨骼层次一般只有一个根关节。
既然关节的方位是定义在父关节空间中的,那如何知道自己的全局方位呢?只要把它的所有父关节的空间矩阵乘起来再乘以它自己的空间矩阵就可以了,如joint2的全局方位矩阵为:G2 = M0*M1*M2,我们把G2称为joint2的全局矩阵(global matrix),这样若要把一个定义在joint2空间中的顶点变换到建模空间,只需要左乘G2即可;若要把定义在模型空间W中的顶点变换到某个关节的子空间,如joint2,我们只要左乘G2的逆:S2=inverse(G2),我们把S2称为joint2的偏移矩阵(offset matrix)。
基于上面的信息,设计了下面的结构来表示骨骼层次:
struct sJoint
{
std::string name_;
int parent_;
MATRIX4X4 localMatrix_;
MATRIX4X4 globalMatrix_;
};上面的结构体表示一个关节,由关节名称、父关节的id(根节点无父关节,可设为-1)、局部空间矩阵以及全局空间矩阵组成,骨骼层次由根关节开始按照父子关系存储在一个sJoint数组中;sJoint中的localMatrix_和globalMatrix_在动画播放中会经常更新,globalMatrix_通过下面的函数可计算得到:
void UpdateGlobalMatrix(sJoint *skeleton, int numJoints)
{
for (int i=0; i<numJoints; ++i)
{
sJoint &joint = skeleton[i];
if (joint.parent_ == -1)
joint.globalMatrix_ = joint.localMatrix_;
else
joint.globalMatrix_ = skeleton[joint.parent_].globalMatrix_*joint.localMatrix_;
}
}3、动画数据的组织
制作动画时,一般会把整个骨架层次画出来,调整成一个初始姿势,又叫绑定姿势,并由这个姿势来制作动画关键帧;每帧中记录了各关节相对于绑定姿势的旋转,平移,缩放,一般只有根关节才有平移跟缩放,其他关节只有旋转。平移可以用三维向量表示,旋转可以用一个四元数表示,暂不考虑缩放,因为基本用不到。假设骨骼层次有30个关节(实际可能更多),一个三维向量占用3*4=12字节,一个四元数用四维向量表示,占用4*4=16字节,这样一个关键帧占用30*28=840字节,平均每个动作10个关键帧的话,保存一个动作就要8400字节,约8KB,看起来不大,但其实还可以压缩。因为关节不一定在每个关键帧中都有不同的状态,甚至有些关节的状态在数个关键帧中都具有相同的状态,如图2(上)所示,图中是某个关节在具有5个关键帧的动画中的状态变化,用A、B表示其状态,可见在前4帧中该关节的状态都是不变的,在第1和第2帧为该关节保存状态是不必要的,图2(下)显示了压缩后的该关节关键帧;采用压缩机制之后,每个关节对应的关键帧数或者同一关节中的平移与旋转关键帧数都可能不一样,所以我们要对每个关节独立保存关键帧,并且每个关节的不同状态也分开保存,这里只有平移和旋转状态。
图2:关键帧压缩
基于上面的分析,动画数据就可以组织成下面的形式:
animation name: walk
total channels: m
total keys: n
total time: xx seconds
channel 0:
translation keys: 0(0,0,0) 2(0,0.5,0.5) n-1(0,0,0)
rotation keys: 0(0,0,0,0) 1(0.5,0.5,0.5,0) 5(0.5,0.5,0.1,0) 8(0.5,0.1,0.5,0) n-1(0.1,0.5,0.5,0)
channel 1:
.....
.....
channel m-1:一个动画数据文件头保存有动画名字、关节数、关键帧数以及动画的持续时间;接着分别为每个关节保存关键帧数据,其中平移和旋转关键帧都分开存,平移key的格式为:frame index(translation vector),旋转key的格式为:frame index(quaternion)。一般从动画制作软件导出的动画格式可能跟上面的不一样,但可以自己写导出插件进行导出,或者用其他的模型导入工具如Assimp进行转化。在程序中通过下面的数据结构处理动画:
// key frame
struct sSklKeyframe
{
float time_; // in seconds
// for position key, the first 3 values of value_ represent the translation
// for rotation key, value_ is a quaternion
VECTOR4D value_;
};
// channel (one bone one channel)
struct sSklChannel
{
std::string boneName_;
std::vector<sSklKeyframe> positionKeys_;
std::vector<sSklKeyframe> rotationKeys_;
};
// animation
struct sAnimation
{
std::string animName_;
std::vector<sSklChannel> channels_;
};从上到下分别表示关键帧,通道(一个关节对应的关键帧的集合),以及动画。有了一个完整的animation关键帧集合,就可以播放该动画了,如果单纯播放关键帧可能会出现动作不平滑的问题,解决方法是帧间平滑插值,见下一节。
4、关键帧之间的平滑插值
假设一个动画有10s,每个整数秒处都设有一个关键帧,那么整数秒之间的骨架状态就通过帧间插值获得;插值的基本思想是:给定一个时间t,找出t处在哪两个关键帧之间,假设为p和q,然后根据p,q处的关节状态和时间t计算出关节在t时间的状态;因为我们每个关节的关键帧是分开存的,因此我们对每个关节也要分开插值,而且对同一个关节的位置和旋转也要分开插值;为了更好的描述之,看下面的伪码:
void Play(sJoint *skeleton, int numJoints, sAnimation &anim, float time)
{
for (int i=0; i<anim.channels_.size(); ++i)
{
sSklChannel &channel = anim.channels_[i];
// find two keys for interpolation
find two position keys pi,pj,in channel.positionKeys_ contain time;
find two rotation keys ri,rj,in channel.rotationKeys_ contain time;
// calculate interp. parameters, pp,rp;
..
// do interpolation
VECTOR3D pos@time = position_interpolate(pi,pj,pp);
VECTOR4D rot@time = rotation_interpolate(ri,rj,rp);
// make a matrix from pos@time and rot@time
MATRIX4X4 animMatrix = MakeMatrix(pos@time,rot@time);
// update local matrix of the bone
int boneId = FindBoneIdByNane(skeleton, numJoints, channel.boneName_);
sJoint &bone = skeleton[boneId];
bone.localMatrix_ = animMatrix;
}
// bones' local matrices were updated, so we update the global matrix
// after that, we got the skeleton state at time t
UpdateGlobalMatrix(skeleton,numJoints);
}下面讨论position_interpolate和rotation_interpolate两个插值函数的实现,插值方法有很多;如线性插值,hermite(埃尔米特)插值,还有球面插值;我们对平移选择hermite插值,对旋转采用四元数球面插值,因为线性插值存在过渡不平滑的问题;具体的实现因为篇幅问题就不深入讨论了。蒙皮动画不能少了皮,我们现在只有骨架的动画,下面介绍软件和硬件蒙皮。
5、软件蒙皮的实现
当骨架的绑定pose调整好之后,就可以给它绑上一层“皮”了,皮就是一个三维网格,如一个人,一只动物等。绑定一般是通过建模软件如maya,3dmax来做的,当然现在也有自动化的绑定工具,有兴趣可以看看07年siggraph上的一篇论文:Automatic rigging and animation of 3d characters。SPE是通过建模工具绑定的,网格被绑之后,网格上的每个顶点都会绑定到一个或者多个(一般不多于4个)对该顶点影响最大的关节上,这些关节的状态变化会按照权重共同影响该顶点的位置变化,总体效果就是皮随着骨架运动。蒙皮的任务就是根据当前骨架状态以及各顶点的绑定信息计算出新的网格顶点坐标。软件蒙皮的伪码如下:
void DrawSkinnedMesh(cObject &object, sJoint *skeleton)
{
for each vertex v in object
{
int *boneIds = v.bones;
float *weights = v.weights;
VECTOR4D vert = v.pos;
VECTOR4D norm = v.norm;
VECTOR4D animedVertex(0,0,0,0),animedNorm(0,0,0,0);
for each bone boneId in boneIds
{
sJoint &joint = skeleton[boneId];
animedVertex += joint.globalMatrix_*joint.offsetMatrix_*vert*weight;
animedNorm += joint.globalMatrix_*joint.offsetMatrix_*norm*weight;
}
v.animedPos = animedVertex;
v.animedNorm = animedNorm;
}
// draw animated skin here....
}struct sJoint
{
std::string name_;
int parent_;
MATRIX4X4 offsetMatrix_; // new added
MATRIX4X4 localMatrix_;
MATRIX4X4 globalMatrix_;
};软件蒙皮工作得很好,但是它在某些情况下比较没有效率,特别是在同一场景中骨骼蒙皮模型很多的时候,例如游戏中一群怪物围着角色攻击,系统既要处理碰撞、AI等其他游戏逻辑又要做动画插值和蒙皮,而蒙皮又是骨骼动画中最耗时的步骤,因此它应该尽可能地被优化。优化最有效的方式就是让GPU处理蒙皮,因为对各顶点的变换是互不相关的,因此完全可以用GPU做并行计算,用顶点着色器(vertex shader)实现,下面是vs的代码:
#version 140
varying vec3 viewPos;
varying vec3 viewNorm;
///
uniform mat4 globalMats[60];
attribute vec4 weights;
attribute vec4 bones;
attribute int numBones;
///
void main()
{
vec4 vert4 = gl_Vertex;
vec4 norm4 = vec4(gl_Normal,0.0);
///
int boneId;
float weight;
vec4 pos = vec4(0.0,0.0,0.0,0.0);
vec4 norm = vec4(0.0,0.0,0.0,0.0);
for (int i=0; i<numBones; ++i)
{
boneId = int(bones.x);
weight = weights.x;
mat4 globalMat = globalMats[boneId];
pos += globalMat*vert4*weight;
norm += globalMat*norm4*weight;
bones = vec4(bones.yzw,bones.x);
weights = vec4(weights.yzw,weights.x);
}
pos.w = 1.0;
norm.w = 0.0;
///
viewNorm = normalize(gl_NormalMatrix * vec3(norm));
viewPos = vec3(gl_ModelViewMatrix * pos);
gl_TexCoord[0] = gl_MultiTexCoord0;
gl_Position = gl_ModelViewProjectionMatrix * pos;
}7、结果
图3:Wuson动画,软件蒙皮
图4:跟上图一样的场景,硬件蒙皮,通过帧率可以看到要快5倍



























 1002
1002

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








