机器人的运动模型

机器人的运动模型

这篇文章主要介绍两轮机器人如何根据:
机器人轮子的编码信息和机器人当先位姿$(x_1,y_1,\theta)$计算出下一时刻机器人的位姿$(x_2,y_2,\theta_2)$。
即：
输入：$(x_1,y_2,\theta_1)$、 机器人左右轮子的间距$w$，码盘的距离信息$l$和$r$
输出：$(x_2,y_2,\theta_2)$
机器人在平面上运动时有两种情况，一种是转弯的情况，另一种是不转弯的情况；
下面分别进行介绍：

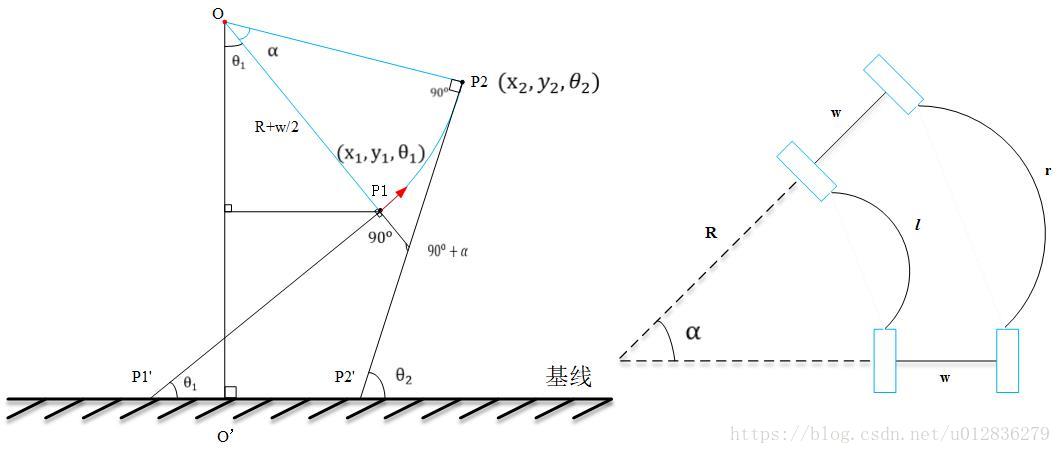
1. 转弯的情况

机器人在转弯的时候，其运动的示意图如下所示，其中角$\angle P1P1'P2'$表示机器人P1点的头朝向，角$\angle P2P2'基线$ 表示机器人在P2点的头朝向。需要注意的是，头朝向$\theta$ 是以$O$为圆心，$R+w/2$为半径的圆的边界引出一条切线和基线之间的形成的夹角的大小。在图中，通过相似三角形的性质可以知道，$\angle P1P1'P2'$ = $\angle O'OP1$ = $\theta_1$
那么角度$\theta2$可以通过四边形OO’P2P2’的内角和为360度得到：

$$\angle O'OP2 + \angle OO'P2' + \angle O'P2'P2 + \angle OP2P2' = 360$$
即
$$(\theta_1+\alpha)+ 90 + (180-\theta_2) + 90 = 360$$
整理之后，得到，
$$\theta_2 = \theta_1+\alpha$$

在中小学的时期，我们学到如下计算周长的公式：

$$C = 2\pi r = r\int_{0}^{2\pi}d\theta$$
由此可知，当 $\theta$的值很小的时候，周长=角度*半径。利用这种思想，我们可以构建如下的公式：
$$\alpha R = l$$ $$\alpha(R+w) = r$$
在上述公式中，只有 $l$和$r$是已经知道的，但是我们可以根据该公式计算出 $\alpha$和 $R$:
$$\alpha = \frac{r-l}{w}$$ $$R = \frac{lw}{r-l}$$
现在已知 $P1(x_1,y_1,\theta_1)$、 $\alpha$、 $R$和轮子之间的间距$w$，如何求 $P2$呢?

假设机器人在转弯的时候是以圆心$O$为中心从$P1(x_1,y_1,\theta_1)$运动到$P2(x_2,y_2,\theta_2)$,
那么圆心的计算公式如下：

$$x_0 + (R+\frac{w}{2})sin(\theta_1) = x_1$$ $$y_0 - (R+\frac{w}{2})cos(\theta_1) = y_1$$
$$\left[ \begin{matrix} x_0 \\ y_0 \end{matrix} \right] = \left[ \begin{matrix} x_1 \\ y_1 \end{matrix} \right] +(R+\frac{w}{2})\left[ \begin{matrix}-sin(\theta_1) \\ cos(\theta_1) \end{matrix} \right]$$

知道圆心和从$P1$到$P2$之间移动角度大小为$\theta_1+\alpha$,那么$P2$的计算方法为：

$$\left[ \begin{matrix} x_0 \\ y_0 \end{matrix} \right] + (R+\frac{w}{2}) \left[ \begin{matrix}cos(\theta_1+\alpha) \\ -sin(\theta_1+\alpha) \end{matrix} \right] = \left[ \begin{matrix} x_2 \\ y_2 \end{matrix} \right]$$

所以此时$P2(x_2,y_2,\theta_2)$的坐标为

$$\left[ \begin{matrix} x_2 \\ y_2 \\ \theta_2\end{matrix} \right] = \left[ \begin{matrix}(R+\frac{w}{2}) cos(\theta_1+\alpha) \\ -(R+\frac{w}{2}) sin(\theta_1+\alpha) \\ \theta_1+\alpha \end{matrix} \right]$$

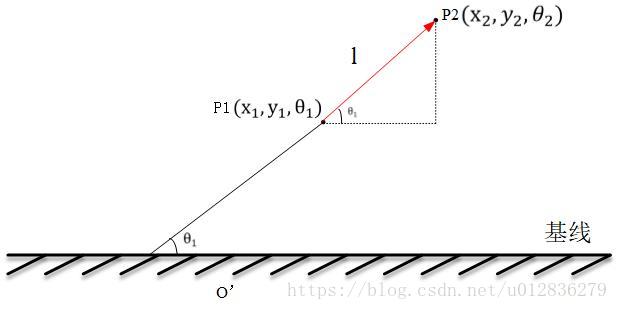
2. 不转弯的情况

当机器人不转弯的时候，机器人位姿中$\theta_1$是不会发生变化的，且$l=r$，所以这时

$$\theta_2 = \theta_1$$
而机器人的位姿会发生的变化如下图所示，

$$\left[ \begin{matrix} x_2 \\ y_2 \end{matrix} \right] = \left[ \begin{matrix} x_1 \\ y_1 \end{matrix} \right] + \left[ \begin{matrix}lcos(\theta_1) \\ lsin(\theta_1) \end{matrix} \right]$$