前面介绍的PID,pure pursuit方法,Stanley方法都只是利用当前的系统误差来设计控制器。人们对这些控制器的设计过程中都利用了构建模型对无人车未来状态的估计(或者说利用模型估计未来的运动趋势)。每个控制周期只选择一个目标路点作为跟踪对象,因此,我们也可以说以上控制器只利用了模型进行向前一步预测。那么如果在更远的未来,参考轨迹变化不是那么平缓,并且有很多弯度小(急)的部分,那么只利用一步预测很难对整条轨迹进行有效的跟踪。为了让无人车的控制器更有前瞻性(远见),设计控制器必须得利用模型对未来状态进行多步预测。本文介绍的模型预测控制(MPC)以及后一篇的线性二次调节(LQR)设计的控制器都基于模型多步预测结果。
基础链接:
无人车系统(一):运动学模型及其线性化
无人车系统(七):Udacity 's无人驾驶仿真环境(社区介绍)
无人车系统(八):Udacity 's无人驾驶仿真环境(python与c++数据接口)
无人车系统(十):c++与python非线性规(优)划(化)工具
相关链接:
无人车系统(四):轨迹跟踪PID控制
无人车系统(五):轨迹跟踪Pure Pursuit方法
无人车系统(六):轨迹跟踪Stanley方法
同时也希望大家多多支持本人第一个付费专栏《自动驾驶规划入门(已完结)》,满足我一点点的虚荣心=v=,里面有更多将pyomo用于路径规划与轨迹规划的案例。
1. 模型预测控制原理
模型预测控制(MPC)的最核心思想就是利用三维的空间模型加上时间构成四维时空模型,然后在这个时空模型的基础上,求解最优控制器。MPC控制器基于一段时间的时空模型,因此得到的控制输出也是系统在未来有限时间步的控制序列。 由于,理论构建的模型与系统真实模型都有误差;从而,更远未来的控制输出对系统控制的价值很低,MPC仅执行输出序列的中第一个控制输出。

假设向前预测步长为 T T T,那么T步的时空模型要比原始的空间模型要大很多。MPC在每个控制周期都需要重新利用未来T步的模型计算得到当前执行的控制指令。MPC利用了一个比原始空间模型大很多的模型(更高的计算成本)仅仅只得到当前一步的最优控制器(跟PID,pure pursuit, stanley做了同样的事)。
3. MPC控制器设计
3.1 线性模型
当模型是线性的形式(或者利用无人车系统(一):运动学模型及其线性化相同的方法对非线性模型进行线性化),MPC控制器的求解问可以转化为一个二次规划问题,
假定线性模型为以下形式:
x
k
+
1
=
A
x
k
+
B
u
k
+
C
(1)
x_{k+1}=Ax_k+Bu_k+C \tag{1}
xk+1=Axk+Buk+C(1)
假定未来
T
T
T步的控制输入已知,为
u
k
,
u
k
+
1
,
u
k
+
2
,
.
.
.
,
u
k
+
T
u_k, u_{k+1}, u_{k+2}, ..., u_{k+T}
uk,uk+1,uk+2,...,uk+T,根据以上模型与输入,我们可以计算未来
T
T
T步的状态:
x
k
+
1
=
A
x
k
+
B
u
k
+
C
x_{k+1}=Ax_k+Bu_k+C
xk+1=Axk+Buk+C
x
k
+
2
=
A
x
k
+
1
+
B
u
k
+
1
+
C
=
A
(
A
x
k
+
B
u
k
+
C
)
+
B
u
k
+
1
+
C
=
A
2
x
k
+
1
+
A
B
u
k
+
B
u
k
+
1
+
A
C
+
C
x_{k+2}=Ax_{k+1}+Bu_{k+1}+C=A(Ax_k+Bu_k+C)+Bu_{k+1}+C=A^2x_{k+1}+ABu_k+Bu_{k+1}+AC+C
xk+2=Axk+1+Buk+1+C=A(Axk+Buk+C)+Buk+1+C=A2xk+1+ABuk+Buk+1+AC+C
x
k
+
3
=
A
3
x
k
+
A
2
B
u
k
+
A
B
k
+
1
+
B
u
k
+
2
+
A
2
C
+
A
C
+
C
x_{k+3}=A^3x_k+A^2Bu_{k}+AB_{k+1}+Bu_{k+2}+A^2C+AC+C
xk+3=A3xk+A2Buk+ABk+1+Buk+2+A2C+AC+C
.
.
.
...
...
x
k
+
T
=
A
T
x
k
+
A
T
−
1
B
u
k
+
A
T
−
2
B
u
k
+
1
+
.
.
.
+
A
T
−
i
B
u
k
+
i
−
1
+
.
.
.
+
B
u
k
+
T
−
1
+
A
T
−
1
C
+
A
T
−
2
C
+
.
.
.
+
C
x_{k+T}=A^{T}x_{k}+A^{T-1}Bu_k+A^{T-2}Bu_{k+1}+...+A^{T-i}Bu_{k+i-1}+...+Bu_{k+T-1}+A^{T-1}C+A^{T-2}C+...+C
xk+T=ATxk+AT−1Buk+AT−2Buk+1+...+AT−iBuk+i−1+...+Buk+T−1+AT−1C+AT−2C+...+C
将上面
T
T
T规划成矩阵向量形式:
X
=
A
x
k
+
B
u
+
C
(2)
\mathcal{X}=\mathcal{A}x_k+\mathcal{B}\mathbf{u}+\mathcal{C} \tag{2}
X=Axk+Bu+C(2)
其中,
X
=
[
x
k
+
1
x
k
+
2
x
k
+
3
.
.
.
x
k
+
T
]
T
\mathcal{X}=\left[\begin{matrix} x_{k+1} & x_{k+2} & x_{k+3}& ... & x_{k+T}\end{matrix}\right]^T
X=[xk+1xk+2xk+3...xk+T]T,
u
=
[
u
k
u
k
+
1
u
k
+
2
.
.
.
u
k
+
T
−
1
]
T
\mathbf{u}=\left[\begin{matrix} u_k & u_{k+1} & u_{k+2} &...&u_{k+T-1}\end{matrix}\right]^T
u=[ukuk+1uk+2...uk+T−1]T,
A
=
[
A
A
2
A
3
.
.
.
A
T
]
T
\mathcal{A}=\left[\begin{matrix}A & A^2 & A^3 & ... & A^T\end{matrix}\right]^T
A=[AA2A3...AT]T,
B
=
[
B
0
0
.
.
.
0
A
B
B
0
.
.
.
0
A
2
B
A
B
B
.
.
.
0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
A
t
−
1
B
A
T
−
2
B
A
T
−
3
B
.
.
.
B
]
\mathcal{B}=\left[\begin{matrix}B & 0 & 0 & ... & 0 \\AB & B & 0 & ... & 0 \\ A^2B & AB & B & ... & 0 \\...& ...&...&...&...\\A^{t-1}B & A^{T-2}B& A^{T-3}B &...&B\end{matrix}\right]
B=
BABA2B...At−1B0BAB...AT−2B00B...AT−3B...............000...B
,
C
=
[
C
A
C
+
C
A
2
C
+
A
C
+
C
.
.
.
A
k
+
T
−
1
C
+
.
.
.
+
C
]
\mathcal{C}=\left[\begin{matrix}C\\AC+C\\A^2C+AC+C\\...\\A^{k+T-1}C+...+C\end{matrix}\right]
C=
CAC+CA2C+AC+C...Ak+T−1C+...+C
假定参考轨迹为
X
‾
=
[
x
‾
k
+
1
x
‾
k
+
2
x
‾
k
+
3
.
.
.
x
‾
k
+
T
]
T
\overline{\mathcal{X}}=\left[\begin{matrix} \overline{x}_{k+1} & \overline{x}_{k+2} & \overline{x}_{k+3}& ... & \overline{x}_{k+T}\end{matrix}\right]^T
X=[xk+1xk+2xk+3...xk+T]T,则MPC的一个简单的目标代价函数如下:
min
J
=
E
T
Q
E
+
u
T
R
u
s.t.
u
m
i
n
≤
u
≤
u
m
a
x
(3)
\min \mathcal{J}=\mathcal{E}^T Q \mathcal{E}+\mathbf{u}^T R \mathbf{u} \\ \text{s.t. } u_{min}\leq \mathbf{u}\leq u_{max} \tag{3}
minJ=ETQE+uTRus.t. umin≤u≤umax(3)
其中,
E
=
X
−
X
‾
=
[
x
k
+
1
−
x
‾
k
+
1
x
k
+
2
−
x
‾
k
+
2
.
.
.
x
k
+
T
−
x
‾
k
+
T
]
T
\mathcal{E}=\mathcal{X}-\overline{\mathcal{X}}=\left[\begin{matrix} x_{k+1}-\overline{x}_{k+1} & x_{k+2}-\overline{x}_{k+2} & ... & x_{k+T}-\overline{x}_{k+T}\end{matrix}\right]^T
E=X−X=[xk+1−xk+1xk+2−xk+2...xk+T−xk+T]T
将式(2)代入式(3),则优化变量仅乘
u
\mathbf{u}
u。以上最优化问题可用二次规划方法求解,得到满足目标代价函数的最优控制序列
u
=
{
u
k
u
k
+
1
u
k
+
2
.
.
.
u
k
+
T
−
1
}
\mathbf{u}=\left\{\begin{matrix} u_k & u_{k+1} & u_{k+2} &...&u_{k+T-1}\end{matrix}\right\}
u={ukuk+1uk+2...uk+T−1}。
当转换成式(3)后,可以利用凸优化库进行求解,例如python的[cvxopt],OSQP: An Operator Splitting Solver for Quadratic Programs(https://github.com/cvxopt/cvxopt)。特别是OSQP的官方文档中所举的重要应用场景就包括MPC,这里有一个官方教程的关于求解MPC控制器的示例:Model predictive control (MPC) for a quadcopter。此处不多讲。
3.2 非线性模型
3.2.1 无人车轨迹跟踪MPC问题
如果模型是非线性的,并且我们不想对其进行线性化(线性化过程损失了模型精度)。此处以无人车的几何运动学模型为例:
x
˙
=
v
c
o
s
(
θ
)
y
˙
=
v
s
i
n
(
θ
)
θ
˙
=
v
t
a
n
(
δ
)
L
v
˙
=
a
(1)
\begin{matrix} \dot{x}=vcos(\theta) \\ \dot{y}=vsin(\theta) \\ \dot{\theta}=v\frac{tan(\delta)}{L} \\ \dot{v}=a \end{matrix} \tag{1}
x˙=vcos(θ)y˙=vsin(θ)θ˙=vLtan(δ)v˙=a(1)
首先我们需要将以上连续的微分模型离散化成差分模型(差分间隔为 d t d_t dt):
x k + 1 = x k + v k cos ( θ k ) d t y k + 1 = y k + v k sin ( θ k ) d t θ k + 1 = θ k + v k tan ( δ k ) L d t v k + 1 = v k + a k d t cte k + 1 = cte k + v k sin ( θ k ) d t epsi k + 1 = epsi k + v k tan ( δ k ) L d t (2) \begin{matrix} x_{k+1}=x_k+v_k\cos(\theta_k)d_t \\ y_{k+1}=y_k+v_k\sin(\theta_k)d_t \\ \theta_{k+1}=\theta_{k}+v_k \frac{\tan(\delta_k)}{L}d_t \\ v_{k+1} = v_k+a_kd_t \\ \text{cte}_{k+1} = \text{cte}_k+v_k \sin (\theta_k)d_t \\ \text{epsi}_{k+1}=\text{epsi}_k+v_k \frac{\tan(\delta_k)}{L}d_t \end{matrix} \tag{2} xk+1=xk+vkcos(θk)dtyk+1=yk+vksin(θk)dtθk+1=θk+vkLtan(δk)dtvk+1=vk+akdtctek+1=ctek+vksin(θk)dtepsik+1=epsik+vkLtan(δk)dt(2)
假定无人车需要跟踪的轨迹是由离散点
{
(
x
‾
1
,
y
‾
1
)
,
(
x
‾
2
,
y
‾
2
)
,
.
.
.
,
(
x
‾
M
,
y
‾
M
)
}
\{(\overline{x}_1, \overline{y}_1), (\overline{x}_2, \overline{y}_2),...,(\overline{x}_M, \overline{y}_{M})\}
{(x1,y1),(x2,y2),...,(xM,yM)}通过三次曲线拟合而成,可表示成由x轴为自变量的函数:
y
=
f
(
x
)
=
c
0
x
3
+
c
1
x
2
+
c
2
x
+
c
3
y=f(x)=c_0 x^3+c_1 x^2+c_2 x+c_3
y=f(x)=c0x3+c1x2+c2x+c3。值得说明的是,表示轨迹的离散点需要转换到车本体坐标系下。
因此,在每一预测步,我们可以根据无人车的
x
k
x_k
xk与
y
k
y_k
yk值计算横向跟踪误差
cte
k
\text{cte}_{k}
ctek与航向偏差
epsi
k
\text{epsi}_k
epsik。横向跟踪误差与航向偏差的介绍请见无人车系统(六):轨迹跟踪Stanley方法。具体计算公式如下:
cte
k
=
f
(
x
k
)
−
y
k
epsi
k
=
a
r
c
tan
(
f
′
(
x
k
)
)
−
θ
(3)
\begin{array}{c} \text{cte}_k=f(x_k)-y_k \\ \text{epsi}_k = arc\tan(f'(x_k))-\theta \end{array} \tag{3}
ctek=f(xk)−ykepsik=arctan(f′(xk))−θ(3)
对于一个预测步长为
N
N
N的MPC控制器求解问题,可以设计以下优化目标函数:
min
J
=
∑
k
=
1
N
(
ω
cte
∣
∣
cte
t
∣
∣
2
+
ω
epsi
∣
∣
epsi
k
∣
∣
2
+
ω
v
∣
∣
v
k
−
v
ref
∣
∣
2
)
+
∑
k
=
1
N
−
1
(
ω
δ
∣
∣
δ
k
∣
∣
2
+
ω
a
∣
∣
a
k
∣
∣
2
)
+
∑
k
=
1
N
−
2
(
ω
rate
δ
∣
∣
δ
k
+
1
−
δ
k
∣
∣
2
+
ω
rate
a
∣
∣
a
k
+
1
−
a
k
∣
∣
2
)
(4)
\begin{array}{cc} \text{min } &\mathcal{J}=\sum_{k=1}^N(\omega_{\text{cte}}||\text{cte}_t||^2+\omega_{\text{epsi}}||\text{epsi}_k||^2+\omega_v ||v_k-v_{\text{ref}}||^2) \\ & +\sum_{k=1}^{N-1}(\omega_{\delta}||\delta_k||^2+\omega_{a}||a_k||^2) \\ & +\sum_{k=1}^{N-2}(\omega_{\text{rate}_{\delta}}||\delta_{k+1}-\delta_{k}||^2+\omega_{\text{rate}_{a}}||a_{k+1}-a_{k}||^2) \\ \end{array}\tag{4}
min J=∑k=1N(ωcte∣∣ctet∣∣2+ωepsi∣∣epsik∣∣2+ωv∣∣vk−vref∣∣2)+∑k=1N−1(ωδ∣∣δk∣∣2+ωa∣∣ak∣∣2)+∑k=1N−2(ωrateδ∣∣δk+1−δk∣∣2+ωratea∣∣ak+1−ak∣∣2)(4)
满足动态模型约束:
s.t.
x
k
+
1
=
x
k
+
v
k
c
o
s
(
θ
k
)
d
t
,
k
=
1
,
2
,
.
.
.
,
N
−
1
y
k
+
1
=
y
k
+
v
k
s
i
n
(
θ
k
)
d
t
,
k
=
1
,
2
,
.
.
.
,
N
−
1
θ
k
+
1
=
θ
k
+
v
k
t
a
n
(
δ
k
)
L
d
t
,
k
=
1
,
2
,
.
.
.
,
N
−
1
v
k
+
1
=
v
k
+
a
k
d
t
,
k
=
1
,
2
,
.
.
.
,
N
−
1
cte
k
+
1
=
f
(
x
k
)
−
y
k
+
v
k
sin
(
θ
k
)
d
t
epsi
k
+
1
=
a
r
c
tan
(
f
′
(
x
k
)
)
−
θ
+
v
k
tan
(
δ
k
)
L
d
t
(5)
\begin{array}{c} \text{s.t.} & x_{k+1}=x_k+v_kcos(\theta_k)d_t , k=1,2,...,N-1\\ & y_{k+1}=y_k+v_ksin(\theta_k)d_t , k=1,2,...,N-1\\ & \theta_{k+1}=\theta_{k}+v_k \frac{tan(\delta_k)}{L}d_t , k=1,2,...,N-1\\ & v_{k+1} = v_k+a_kd_t, k=1,2,...,N-1 \\ & \text{cte}_{k+1} =f(x_k)-y_k+v_k \sin (\theta_k)d_t \\ & \text{epsi}_{k+1}=arc\tan(f'(x_k))-\theta+v_k \frac{\tan(\delta_k)}{L}d_t \end{array}\tag{5}
s.t.xk+1=xk+vkcos(θk)dt,k=1,2,...,N−1yk+1=yk+vksin(θk)dt,k=1,2,...,N−1θk+1=θk+vkLtan(δk)dt,k=1,2,...,N−1vk+1=vk+akdt,k=1,2,...,N−1ctek+1=f(xk)−yk+vksin(θk)dtepsik+1=arctan(f′(xk))−θ+vkLtan(δk)dt(5)
执行器约束:
δ ∈ [ δ min , δ max ] a ∈ [ a min , a max ] (6) \begin{array}{cc} \delta\in[\delta_{\text{min}}, \delta_{\text{max}}]\\ a\in [a_{\text{min}}, a_{\text{max}}] \end{array}\tag{6} δ∈[δmin,δmax]a∈[amin,amax](6)
式(4)、(5)、(6)构成无人车轨迹跟踪的完整控制问题。
那么一个问题来了,这样的模型,像条件中还带正弦、余弦函数,这怎么求解?
3.2.2 无人车轨迹跟踪MPC问题求解
3.2.2.1 其于CppAD的实现
前面一篇博客无人车系统(十):c++与python非线性规(优)划(化)工具可以完美求解这种非线性形式的问题,而且一点也不麻烦。
C++与CppAD的版本已经由DhruvaKumar/model-predictive-control,大家可以git下来跑的试试,怎么安装的按照教程走就行。编译过程可能会遇到如下错误:
src/json.hpp:6057:62: error: wrong number o
这个错误,我是通过更换src/json.hpp文件解决的。大家去百度网盘下载json.hpp替换项目src目录下的老版json.hpp即可。下载地址:https://pan.baidu.com/s/1Szza1CiOVlw2ULf_qUDNew [提取码 9osc]。
编译成功后,运行程序出现以下错误:
error while loading shared libraries: libcoinmumps.so.1: cannot open shared对于这个错误,是因为系统是64位的,但是程序用到的某个32版本的库。我运行以下命令就解决了。
sudo apt-get update
sudo apt-get install ia32-libs
或
sudo apt-get install lib32z1
更多问题解决请参照:Udacity-selfdriving car nanodegree复现遇到的问题及解决办法
3.2.2.2 基于python+pyomo的实现
这些天一直在找基于python的实现方法,主要有两个目的:1)深刻理解MPC;2)python编程太方便了。
发现python+pyomo可以完美解决这个问题。
下面是基于pyomo构建的无人车轨迹跟踪问题的求解模型。
import numpy as np
from pyomo.environ import *
from pyomo.dae import *
N = 9 # forward predict steps
ns = 6 # state numbers / here: 1: x, 2: y, 3: psi, 4: v, 5: cte, 6: epsi
na = 2 # actuator numbers /here: 1: steering angle, 2: throttle
class MPC(object):
def __init__(self):
m = ConcreteModel()
m.sk = RangeSet(0, N-1)
m.uk = RangeSet(0, N-2)
m.uk1 = RangeSet(0, N-3)
# Parameters
m.wg = Param(RangeSet(0, 3), initialize={0:1., 1:10., 2:100., 3:130000}, mutable=True)
m.dt = Param(initialize=0.1, mutable=True)
m.Lf = Param(initialize=2.67, mutable=True)
m.ref_v = Param(initialize=75., mutable=True)
m.ref_cte = Param(initialize=0.0, mutable=True)
m.ref_epsi = Param(initialize=0.0, mutable=True)
m.s0 = Param(RangeSet(0, ns-1), initialize={0:0., 1:0., 2:0., 3:0., 4:0., 5:0.}, mutable=True)
m.coeffs = Param(RangeSet(0, 3),
initialize={0:-0.000458316, 1:0.00734257, 2:0.0538795, 3:0.080728}, mutable=True)
# Variables
m.s = Var(RangeSet(0, ns-1), m.sk)
m.f = Var(m.sk)
m.psides = Var(m.sk)
m.ua = Var(m.uk, bounds=(-1.0, 1.0))
m.ud = Var(m.uk, bounds=(-0.436332, 0.436332))
# 0: x, 1: y, 2: psi, 3: v, 4: cte, 5: epsi
# Constrainsts
m.s0_update = Constraint(RangeSet(0, ns-1), rule = lambda m, i: m.s[i,0] == m.s0[i])
m.x_update = Constraint(m.sk, rule=lambda m, k:
m.s[0,k+1]==m.s[0,k]+m.s[3,k]*cos(m.s[2,k])*m.dt
if k<N-1 else Constraint.Skip)
m.y_update = Constraint(m.sk, rule=lambda m, k:
m.s[1,k+1]==m.s[1,k]+m.s[3,k]*sin(m.s[2,k])*m.dt
if k<N-1 else Constraint.Skip)
m.psi_update = Constraint(m.sk, rule=lambda m, k:
m.s[2,k+1]==m.s[2,k]-m.s[3,k]*m.ud[k]/m.Lf*m.dt
if k<N-1 else Constraint.Skip)
m.v_update = Constraint(m.sk, rule=lambda m, k:
m.s[3,k+1]==m.s[3,k]+m.ua[k]*m.dt
if k<N-1 else Constraint.Skip)
m.f_update = Constraint(m.sk, rule=lambda m, k:
m.f[k]==m.coeffs[0]*m.s[0,k]**3+m.coeffs[1]*m.s[0,k]**2+
m.coeffs[2]*m.s[0,k]+m.coeffs[3])
m.psides_update = Constraint(m.sk, rule=lambda m, k:
m.psides[k]==atan(3*m.coeffs[0]*m.s[0,k]**2
+2*m.coeffs[1]*m.s[0,k]+m.coeffs[2]))
m.cte_update = Constraint(m.sk, rule=lambda m, k:
m.s[4,k+1]==(m.f[k]-m.s[1,k]+m.s[3,k]*sin(m.s[5,k])*m.dt)
if k<N-1 else Constraint.Skip)
# 下面这行代码与上面的公式多了个负号,这是因为udapcity的无人车仿真环境的方向盘(注意不是航向角)往左打为负,往右打为正,正好与坐标系的航向角相反(右手定则,左正右负)
m.epsi_update = Constraint(m.sk, rule=lambda m, k:
m.s[5, k+1]==m.s[2,k]-m.psides[k]-m.s[3,k]*m.ud[k]/m.Lf*m.dt
if k<N-1 else Constraint.Skip)
# Objective function
m.cteobj = m.wg[2]*sum((m.s[4,k]-m.ref_cte)**2 for k in m.sk)
m.epsiobj = m.wg[2]*sum((m.s[5,k]-m.ref_epsi)**2 for k in m.sk)
m.vobj = m.wg[0]*sum((m.s[3,k]-m.ref_v)**2 for k in m.sk)
m.udobj = m.wg[1]*sum(m.ud[k]**2 for k in m.uk)
m.uaobj = m.wg[1]*sum(m.ua[k]**2 for k in m.uk)
m.sudobj = m.wg[3]*sum((m.ud[k+1]-m.ud[k])**2 for k in m.uk1)
m.suaobj = m.wg[2]*sum((m.ua[k+1]-m.ua[k])**2 for k in m.uk1)
m.obj = Objective(expr = m.cteobj+m.epsiobj+m.vobj+m.udobj+m.uaobj+m.sudobj+m.suaobj, sense=minimize)
self.iN = m#.create_instance()
def Solve(self, state, coeffs):
self.iN.s0.reconstruct({0:state[0], 1: state[1], 2:state[2], 3:state[3], 4:state[4], 5:state[5]})
self.iN.coeffs.reconstruct({0:coeffs[0], 1:coeffs[1], 2:coeffs[2], 3:coeffs[3]})
self.iN.f_update.reconstruct()
self.iN.s0_update.reconstruct()
self.iN.psides_update.reconstruct()
SolverFactory('ipopt').solve(self.iN)
x_pred_vals = [self.iN.s[0,k]() for k in self.iN.sk]
y_pred_vals = [self.iN.s[1,k]() for k in self.iN.sk]
steering_angle = self.iN.ud[0]()
throttle = self.iN.ua[0]()
return x_pred_vals, y_pred_vals, steering_angle, throttle
结果和CppAD实现的效果一样,能够完成对轨迹的跟踪。
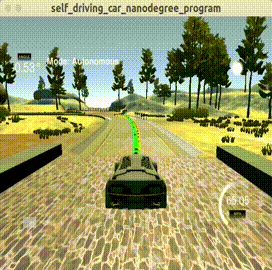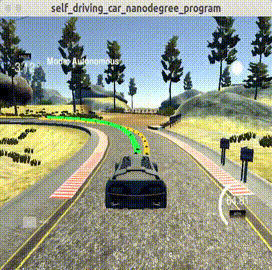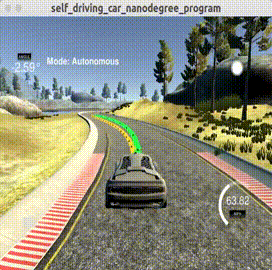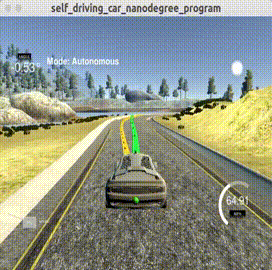
上图黄色曲线为无人车要跟踪的轨迹,绿色曲线为MPC计算出的最优跟踪轨迹。每次MPC求解得到
N
N
N步的控制命令,但是只利用当前步的结果,后面步的扔掉。所以,MPC的更新周期与执行器的更新周期是一致的。
CppAD与pyomo解决无人车轨迹跟踪问题的时间成本都低于0.1s(我电脑配置matebook 14 i5+mx250),其本満足高速运行条件下的无人车高频刷新要求。所以说,MPC的计算成本也没有想象中那么不可接受。
本部分仿真环境是利用进入Udacity‘s simulator的Term 2 SImulator。完整代码需要加上与仿真环境通讯主体代码,具体请看无人车系统(八):Udacity 's无人驾驶仿真环境(python与c++数据接口)。
结语
本篇主要介绍无人车轨迹跟踪MPC控制问题求解方法,为了尽量减少模型的损失,我们利用无人车几何运动学模型构建了MPC问题模型。然后该问题可以通过CppAD或pyomo两种库求解。其中,前者已经在DhruvaKumar/model-predictive-control被实现,本文最后只给出基于pyomo的实现。我们发现,无人车在速度高达将近70MPH(迈)(约113公里/小时,约30米/秒)下能够较好的跟踪轨迹,这足以说明MPC轨迹跟踪控制的稳定与有效性。
PID控制存在积分环节,控制时具有滞后性,而自动驾驶技术对实时性的要求非常高,因此PID控制不太适用于自动驾驶技术。本文介绍的是一种基于模型预测的自动驾驶汽车轨迹追踪方法,不存在滞后性。PID的参数kp,ki,kd与MPC的成本函数中的各权重都需要根据实际应用场景进行调参。
以上
by windSeS 2019-12-20


























 2702
2702

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










