现代机器人技术（二、构形空间）

1.基本概述

基本知识：机器人的机械结构是通过使用各种类型的关节（joints），将一组称为连杆（links）的物体相互连接起来。执行器（actuator）提供了使得机器人连杆运动的力或者力矩。末端执行器（end-effector）(比如抓握和操纵物体的手)附着在特定的连杆上。

构形空间：关于机器人的构形空间，其根本问题是回答机器人在哪里？以下为三个例子。

	门的构形可以由1个数字表示，围绕其铰链的角度θ表示。其构形空间就是【0，2π】
	平面上的点的构形可以由两个坐标（x，y）描述。其构形空间就是能达到所有点的位置坐标集合。
	躺在平桌上的硬币的构形可以通过三个坐标来描述：两个坐标（x，y）指定了硬币上特定点的位置，一个坐标（θ）指定了硬币的方向。其构形空间就是所有（x,y,θ）坐标的集合

定义2.1：机器人的构形（configuration）是对机器人各点位置的完整描述。表示构形所需的最小实值坐标数n为机器人的自由度（dof）。包含机器人所有可能构形的n维空间称为构形空间（C-空间）。机器人的构形由其C空间中的一个点表示。

个人理解：C空间是一个数学模型，它把机器人的位置和姿态用一组参数来表示。这些参数可以是关节的角度、位置坐标或者其他描述机器人状态的变量。

2.1 刚体的自由度

（刚体：在运动中和受力作用后，形状和大小不变，而且内部各点的相对位置不变的物体。刚体自由度就是描述这个刚体需要用到最少的位置坐标的数量）

此图为书中自由度公式推导图示，详细可查看文末链接

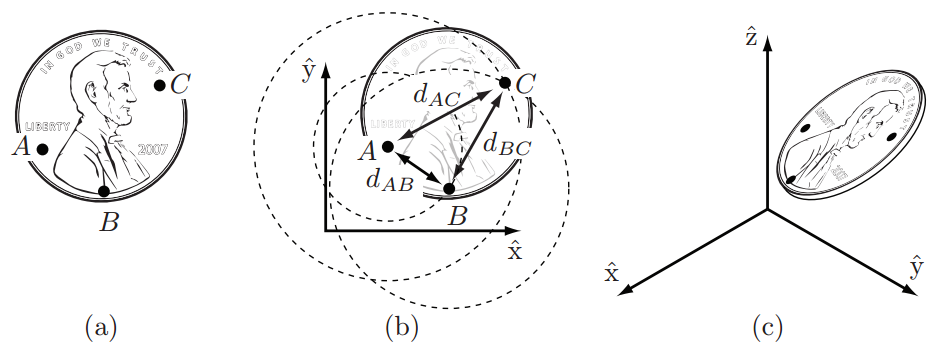
一个在三维空间中运动的刚体，我们称之为空间刚体，有六个自由度。类似地，在二维平面中运动的刚体，我们称之为平面刚体，有三个自由度。

刚体自由度计算公式：自由度 = 自由度之和 - 独立约束的数量。

2.2 机器人的自由度

以这个门为例，前面提到这个门只有一个自由度。但我们想象一下，这个门实际上是通过一个铰链接头（关节）与墙壁连接。没有这个铰链，门相当于是一个空间刚体，具有6个自由度。但是由于铰链的存在，对门的运动施加了五个独立的约束，仅留下一个独立的坐标（θ）。

在上面这扇门的情况中，我们可以知道关节限制了刚体的自由度，从而较低了整体的自由度。由此我们清楚，可以通过计算刚体（增加自由度）和关节（减少自由度）的数量来确定机器人自由度的数量。前面介绍完刚体，下面我们开始介绍关节。

2.2.1 机器人的关节

典型的机器人关节

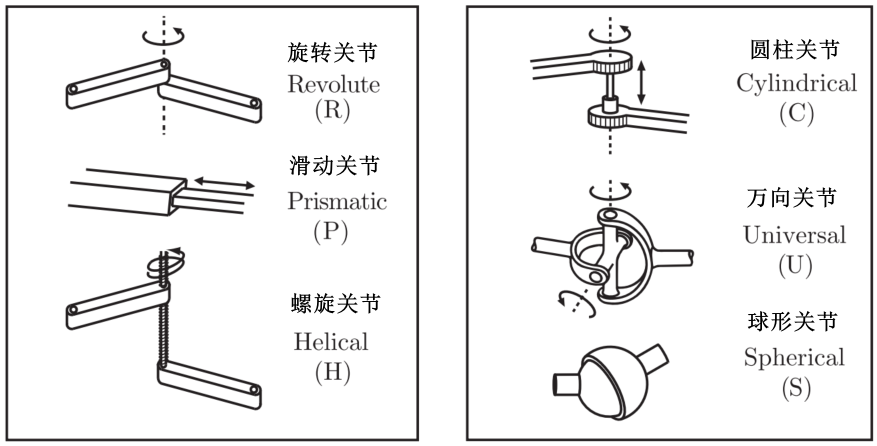
值得注意的是，我们可以将可以将关节视为提供自由度，以使一个刚性的身体相对于另一个身体移动；它也可以看作是对其连接的两个刚体的可能动作提供约束；

典型关节的自由度数量

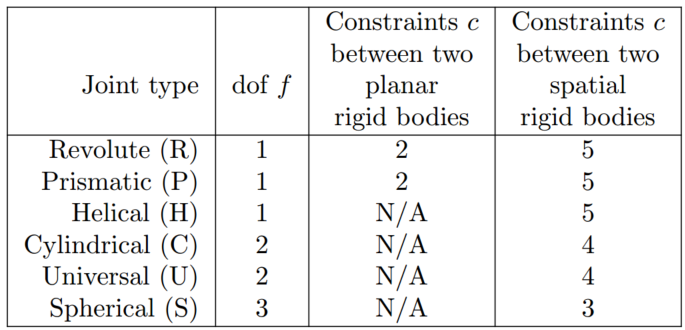
这个表中也同样提到，不仅提到了每个关节的自由度数量，同时也说明了该关节对刚体提供的约束。同时，需要满足关节的自由度的数量与关节提供约束的数量，要等于平面刚体或者空间刚体数量的总和。

（个人理解：关节连接两个刚体，关节的自由度就是一个刚体相对于另一个刚体运动的自由度；如旋转关节中，一个刚体相对于另一个刚体只能旋转，所以只有一个自由度）

2.2.2 Gubler 公式

m(对于平面刚体的m = 3，空间刚体m = 6)；N(连杆的数量)；J（关节的数量）；ci(关节i提供约束的数量)；fi(关节i提供自由度的数量)；fi+ci=m. 为何要N-1？这里我的理解是，机器人通常有个固定的基座，不参与运动，需要减去。

开链机构：没有形成闭合回路的机构（如串联机构，想象人体的一只手臂在空间中自由摆动）

闭链机构：形成闭合回路的机构（想象一下，人体的左右两只手臂，手挽手形成一个闭合的回路）

	看上去，这个机构是三连杆机构，但实际上需要把地面也算上，地面是一个固定的连杆,所以是一个4连杆机构，具有4个关节。所以根据Gubler公式计算： 3*(4 - 1 - 4) + 4 = 1 （平面机构，m=3;旋转关节，fi=1）
	可以看作四连杆机构（滑块和地面分别都是单独的连杆），4个关节（三个旋转，一个滑动）自由度计算： 3*(4-1- 4) + 4 = 1

练习：

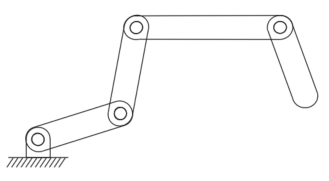	平面机构，m =3；五连杆，N=5；四关节，J=4；都是旋转关节，fi=1；此为开链机构 计算：3*(5-1-4)+4*1=4
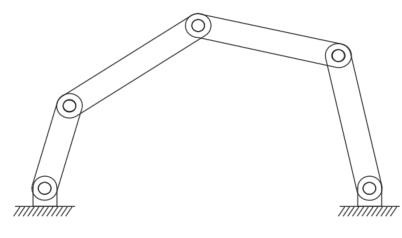	平面机构，m =3；五连杆，N=5；五关节，J=5；都是旋转关节，fi=1；此为闭链机构。 计算：3*(5-1-5)+5*1=2
	平面机构，m =3；六连杆(地面看作一个整体连杆)，N=6；七关节，J=7；都是旋转关节，fi=1；此为闭链机构。 计算：3*(6-1-7)+7 =1
	平面机构，m =3；六连杆(地面看作一个整体连杆)，N=6；七关节，J=7；都是旋转关节，fi=1；此为闭链机构。 计算：3*(6-1-7)+7 =1
	平面机构，m =3；八连杆(地面看作一个整体连杆)，N=8；九关节，J=9；八个旋转关节，一个滑动关节，fi都=1；此为闭链机构。 计算：3*(8-1-9)+9=3

特殊情况：

	如果用公式计算： 3*5(5-1-6)+6=0,发现该机构自由度为0(自由度为零，称之为刚性结构)；但是，显然该机构是可以进行一个自由度的运动的，这里我们要排除冗余约束的连杆和关节（即有没有它运动照样进行），重新计算： 3*（4-1-4）+4=1
	如果连接到地面的两个接头以某种固定角度锁定，则五杆连杆应成为刚性结构；如果两个中间链接的长度相同并相互重叠，这些重叠的链接可以在两个重叠的接头上自由旋转。这里称之为机器人的奇异点，会导致自由度丢失，控制失效

典型机器人：Delta 机器人和多自由度平台

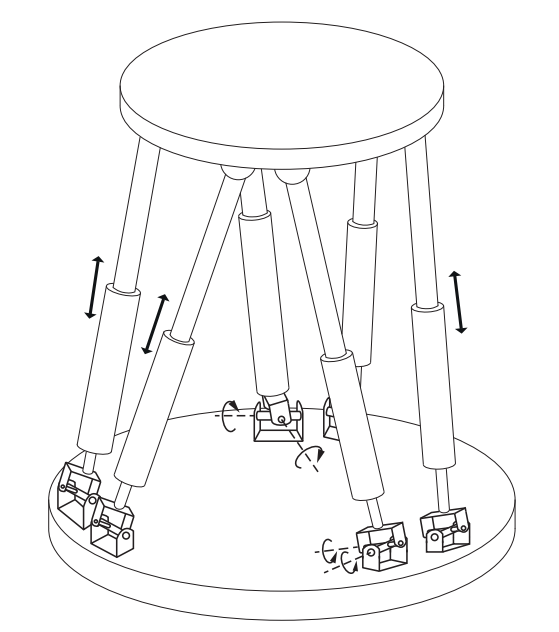
	主要组成：上平板(固定)，下平板（可动），三条腿。 每条腿：包含3个旋转关节，4个球形关节，5根连杆。 由此可得，一共2+3*5=17根连杆，N=17；一共21个关节(9个旋转关节，12个球形关节)，J=21；空间刚体m=6； 根据公式：6*(17-1-21)+9*1+12*3=15 但实际上，移动平台上的末端执行器中只有3个自由度（x-y-z方向上的平移），其他12个内部自由度是通过平行四边形中的12个连杆的扭转（三个腿中的每一个都有四个连杆的扭转），平行四边形的腿部设计可确保移动平台始终保持与固定平台平行
	组成：14个连杆，18个(6个万向关节，6个滑动关节，6个球形关节) 自由度计算: 6*(14-1-18)+6*2+6*1+6*3=6

2.3 构形空间：拓扑和表示形式

2.3.1 构形空间拓扑

前面，我们一直在学习机器人的C空间(关注其维度和自由度)，这里我们注意到，空间的形状也是非常重要的。

考虑一个问题：在球体表面上移动的点。点的C空间是二维的，因为构形可以通过两个坐标，纬度和经度描述。作为另一个例子，在平面上移动的点也具有二维C空间，坐标（x，y）。虽然平面和球的表面都是二维的，但显然它们的形状并不相同。

空间的拓扑是该空间本身的基本属性；例如，为了表示圆上的一个点，我们可以通过从圆的中心到点的角度θ提到点θ，相对于选择的零角度。或者，我们可以选择一个带有其原点位于圆的中心的参考框架，并以约束x^2 + y^2 = 1的约束表示要点。无论我们选择的坐标选择是什么，空间本身都不会改变.

这一块我没有去理解得很深，详细的推导和说明，大家可以看看原著，值得注意的是，拓扑学对于构形空间的表示非常重要。

2.4 构形与速度限制 

我们首先考虑一个四连杆机构

	左图中的四连杆机构，可以由以下三个方程进行表示： x方向方程：各杆在x轴方向的投影之和为零。 y方向方程：各杆在y轴方向的投影之和为零。 角度和条件：四个杆的转角之和为2π，确保闭合性。

对于包含一个或多个封闭环的通用机器人，可以通过列向量隐式表示构形空间：

 形成的闭环方程：

 其中，k指的是k个独立方程（这里应该指的是k个独立回路方程），上述闭环方程对两边进行求导可得：

 因此：

可以简写成：

 最终简化：
 

 其中A(θ)是g(θ)对θ的导数，同时g(θ)又是A(θ)的积分。

现在考虑一枚在在平面上滚动的直立硬币：

 硬币的构形空间由四个参数描述，平面上的接触点（x,y）,转向角φ和旋转角度θ。现在假设硬币只能滚动不滑动，因此可以得到以下关系：

 描述构形空间的四个参数可表示为：

前面我们已经知道

写成矩阵形式：1 * ẋ + 0 * ẏ + 0 * φ̇ + (-r cos φ) * θ̇ = 0；0 * ẋ + 1 * ẏ + 0 * φ̇ + (-r sin φ) * θ̇ = 0

即：

 最终可得：

最终就化简成了A(q) = 0的形式，其中A(q)是2x4的实数矩阵。根据我们原先的推导，将矩阵的各项进行积分：

我们通过观察可以发现，这些条件之间是矛盾的，因此 不存在这样的函数 g1​(q)。由于约束不可积，这些约束被称为 非完整约束（nonholonomic constraints）。非完整约束的特点是：

• 它们限制了系统的 速度（velocity），但 不减少系统可达的配置空间（C-space）的维度。

• 系统仍然可以在整个配置空间中移动，尽管其速度受到约束。

非完整约束在机器人学和控制理论中非常重要，因为它们描述了系统的动态行为，但允许系统在全局范围内具有较高的灵活性。例如：

• 汽车的转向和移动受到非完整约束（车轮不能横向滑动）。

• 移动机器人可以在平面上任意位置，但其速度受到轮子旋转的限制。

对非完整约束的个人理解：
非完整约束就像是给系统设置了一些“限制”，但这些限制并不会完全阻止系统到达某个位置，只是限制了它在移动过程中的方式。在硬币滚动的例子中，硬币不能滑动，只能沿着接触点滚动。这限制了它的速度方向，但它仍然可以在平面上的任何位置以任何角度停下来。这种约束就是非完整约束。

2.5 任务空间和工作空间

任务空间是一个可以自然表达的机器人任务的空间。例如，如果机器人的任务是用笔在纸上绘制，那么任务空间将为r 2。如果任务是操纵刚性的身体，那么任务空间的自然表示是刚体的C空间，代表机器人最终效果图的框架的位置和方向。这是任务空间的默认表示。如何定义任务空间的决定是由任务驱动的，独立于机器人。
工作空间是机器人末端执行器可以达到的构形的范围。工作空间的定义主要由机器人的结构驱动，而不是任务。

下图为各种机器人的工作空间表示：

2.6 参考文献

https://hades.mech.northwestern.edu/images/0/0c/MR-tablet-v2.pdfhttps://hades.mech.northwestern.edu/images/0/0c/MR-tablet-v2.pdf

MODERN ROBOTICS MECHANICS, PLANNING, AND CONTROL-Kevin M. Lynch and Frank C