「自控原理」2.1 控制系统的时域数学模型

本节介绍数学模型的基础知识。引入控制系统的时域数学模型——微分方程，并介绍其构建、使用方法

---

引言

$什么是数学模型?$

数学模型是描述系统输入、输出变量以及内部各变量之间关系的数学表达式。
直观来说就是一个公式，可以通过这个公式，用一部分变量求解另一部分变量。

$数学模型的建模方法$

1. 解析法（机理分析法）
   也就是了解系统的机理，根据系统工作时的物理定律写出方程。
   比如已知输入输出之间接了R电阻，那么根据欧姆定律就有：U_入-U_出=I ·R
2. 实验法（系统辨识法）
   也就是给系统施加测试信号，记录输出响应，并用适当的数学模型去逼近系统的输入输出特性。
   比如有一个黑箱，输入1时输出1，输入0时输出0，虽然不知道系统内部的原理，但依然可以用U_出=U_入来描述这个系统。所以这个方法也被称为黑箱建模法

$控制系统的数学模型$

1. 时域模型——微分方程
2. 复域模型——传递函数

时域模型和复域模型本质上是一样的。只是微分方程求解往往比较困难，所以常转换到复域，利用传递函数描述系统。

控制系统的时域模型——微分方程

线性定常系统微分方程的一般形式

线性：即满足叠加定理。也就是方程没有常数项，且一侧只包含输入及其导数而另一侧只包含输出及其导数。
定常：方程各项的系数都是常数。
在这个系列文章中，“R”表示输入（ru的首字母）
“C”表示输出（chu的首字母）

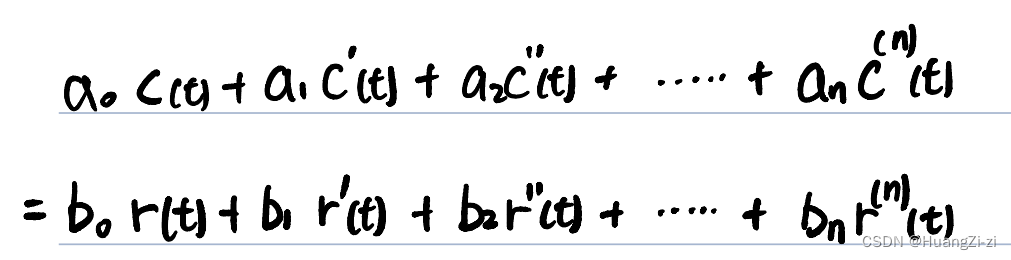
几个典型的例子

RLC电路系统

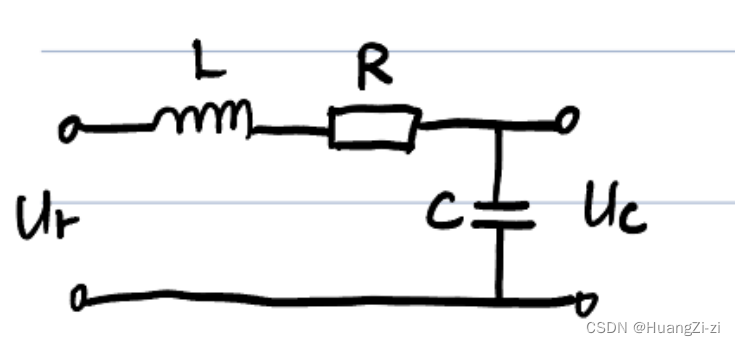
要探究输入电压与输出电压之间的关系，就需要利用到电路里面的基本定理。

首先回路电压之和为零，可以得到关于输入和输出的一个方程。然后按照各个元件的特性进行分析。在这里电流I是一个中间变量，所以应该尽量用输入或者输出量将其表示，然后代入最基础的等式化简得到微分方程。
至于最后进行同时除LC的整理，因为$\frac{L}{R}$和$RC$的量纲都是“秒（s）”，因此也称这两个量为电路网络的时间常数。时间常数决定了方程的解，也就决定了电容上电压（U_c）随时间变化的快慢。
整理后的方程也就可以化成如下的形式：

（可以使方程更加简洁，物理意义更加清晰）

机械动力学系统

上下两个弹簧，中间接一个阻尼器，输入量为阻尼器上方位移输出量为阻尼器下方位移

其中，阻尼力是指阻尼器产生的黏性摩擦阻力，其大小与阻尼器中活塞和缸体的相对运动速度成正比。f为阻尼系数。
阻尼器本身不存储任何动能和势能，主要用来吸收系统的能量。默认情景为平衡状态，也就是作用在阻尼器上下的力相同，刚好等于内部的黏性摩擦阻力。
同样消去中间变量X_m。首先联立F_r=F_c，得到X_m的表达式，然后求导得到X_m’的表达式。然后联立F_f=F_c，再次得到X_m’的表达式，两式恒等得到关于输入和输出的方程。同样进行化简，是因为$\frac{f}{k}$的量纲为秒（s）

更加复杂的系统建立微分方程可能会更加复杂，但基本思路是一样的，根据物理原理列出元件的相关方程，消去中间变量，得到输入和输出之间的关系。

非线性系统微分方程的线性化

一般来说并不讨论过多的非线性系统的内容。所以这些内容只是浅浅略过一下。非线性系统要建立线性的微分方程，可以利用泰勒展开的方法：

微分方程的求解

利用拉氏变换，用留数法分解，再用查表法解方程
「自控原理」1.2 复变知识回顾
这里以例题的形式进行讲解

要求开关闭合后响应的函数

如果直接看微分方程，要解出U_c是非常困难的。但是如果进行拉氏变换，再反变换回来，就可以比较方便的求出U_c了。