文章目录
前言
本文为GAMES101现代计算机图形学入门 的学习笔记系列。
我们的系列笔记将分为两部分:
- 课堂笔记
- 作业
原课程为2020年2月闫令琪所教授的 GAMES101 现代计算机图形学入门。
课程主页:https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html
(幻灯片和课程录像均在此处)
课程共计22节。作业共计8次。
针对人群:计算机图形学入门新手
教材:
Steve Marschner and Peter Shirley的"Fundamentals of Computer Graphics"
第三版或更新版本。目前无官方中文版。
民间翻译:https://www.stubbornhuang.com/1812/
正文
2022-6-5
本节课内容:
- 3D变换(续)
- 视图变换
- 投影变换
– 正交投影
– 透视投影
3D变换(续)
绕xyz轴旋转(欧拉角)
绕x y z轴旋转

可见几乎与2D旋转一致。只是绕哪个轴第几行就为1。例如绕x轴则第一行为[1 0 0]
这是因为绕x轴旋转的时候,要保证x坐标不变
注意绕Y轴,负号位置在左下角。
这样将绕坐标轴旋转复合起来,就可以得到任何的旋转。
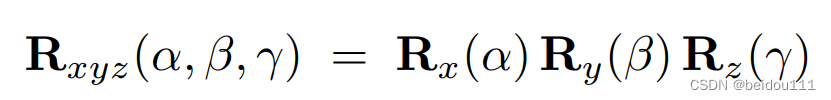
复合起来的三个角度,叫做欧拉角。它可以应用于飞机的转角上,例如
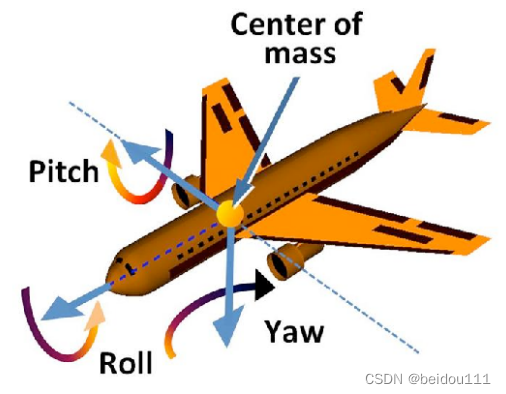
三个角度在航空领域也叫roll pitch yaw
绕任意轴旋转(Rodrigues’ Law)
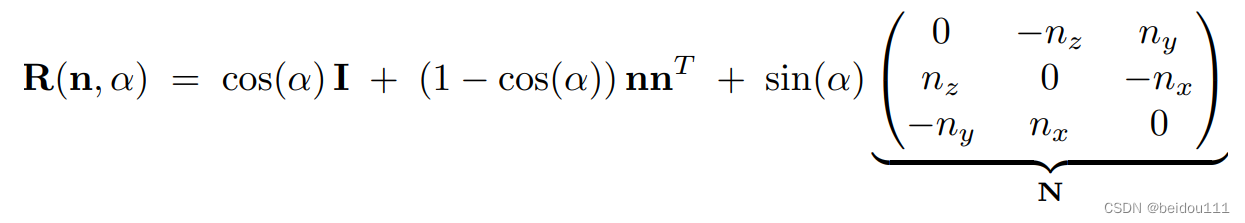
其中轴是n=(nx ny nz) 转角是alpha
这里默认轴过原点
如果轴不过原点,就先把轴平移到原点,再旋转,再平移回去
其中那个矩阵N恰好就是向量n的dual matrix(叉乘的时候将前面的向量写成的那个矩阵)
视图变换(相机变换)
拍照有两步:
- 把物体摆好位置(模型变换)
- 相机找好视角(视图变换)
所以视图变换就是摆放相机
相机标准位置的规定
如何摆放相机?需要定义三个参数:
- 位置 position: e ⃗ \vec e e
- 看向哪 look-at: g ^ \hat g g^ (gaze)
- 头顶在哪 up direction: t ^ \hat t t^ (top)
up direction总与look-at相垂直
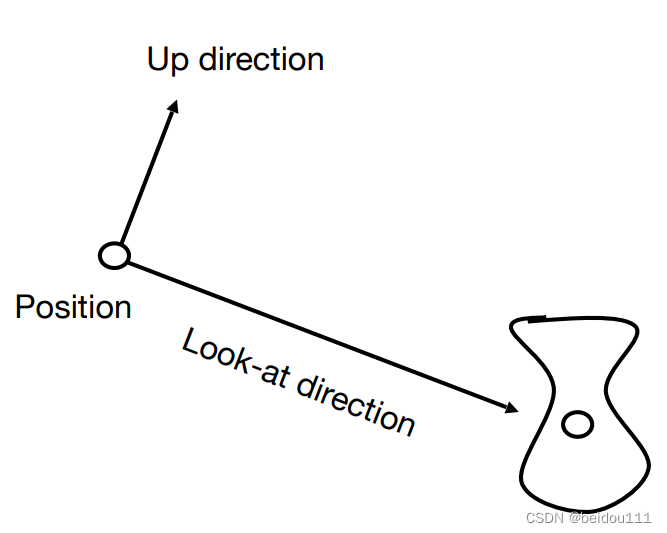
我们可以约定一个相机的标准位置,规定:
- 在原点
- 沿着-z轴方向看
- 头顶沿着y轴方向
将相机变换到标准位置
如果相机不处于标准位置,我们通常将其先变换到标准位置:
例如目前是
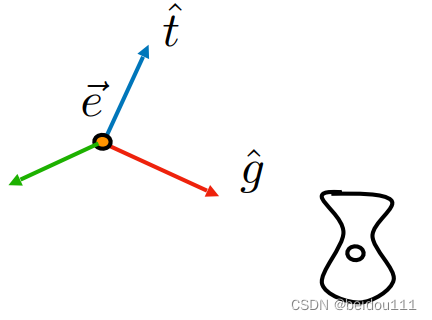
希望变换后是
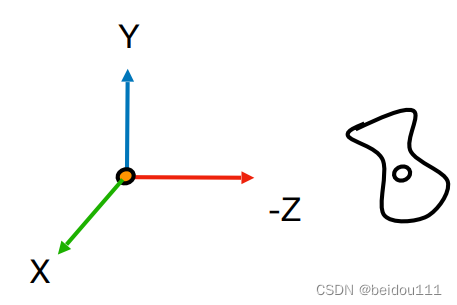
需要经过如下步骤:
- 平移到原点
- 旋转g到-z方向
- 旋转t到y方向
- 旋转 g ^ × t ^ \hat g \times \hat t g^×t^ 到x方向
将其写为变换矩阵
- 先平移
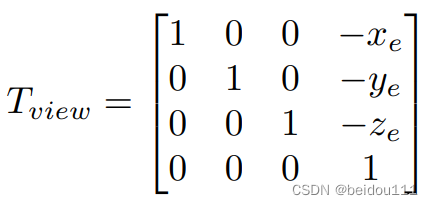
- 再旋转
如何将任意方向的g旋转到-z=(0, 0, -1)方向呢?
直接写是不好找到旋转矩阵的,但是我们可以找到其逆变换:从(0,0,-1)旋转到任意方向g,然后再对矩阵取逆就可以了。
同理,对t的旋转和对
g
^
×
t
^
\hat g \times \hat t
g^×t^ 的旋转都是如此。我们可以直接写到一起,得到旋转矩阵的逆矩阵:
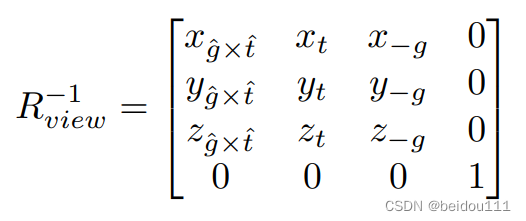
可见该矩阵的第一列恰好就是将 x轴旋转到
g
^
×
t
^
\hat g \times \hat t
g^×t^方向,
第二列恰好就是将y轴旋转到t方向
第三列恰好就是将z轴旋转到-g方向(相当于将-z轴旋转到g方向)
再对它取逆即可(由于旋转矩阵是正交阵,取逆恰好就是取转置)
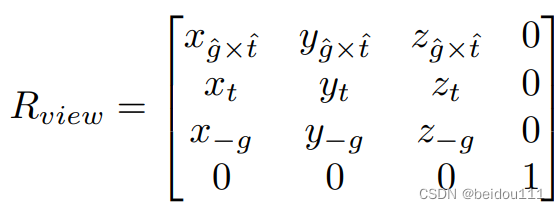
模型视图变换
由于模型变换是对物体进行变换
而视图变换虽然是对相机进行变换,但是也是施加到物体上的
所以两者可以合起来,称为模型视图变换(ModelView)
投影变换
投影分两种:正交投影和透视投影
如图所示
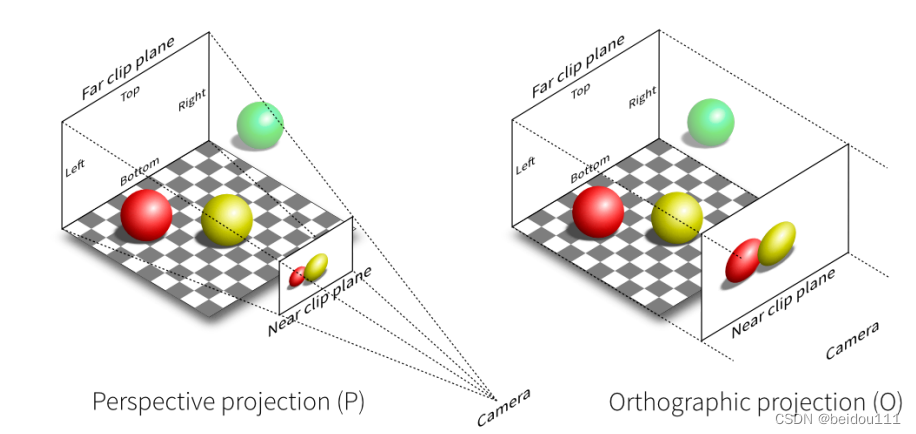
正交投影
- 将相机放到标准位置(位于原点,y轴为上,看向-z)
- 丢掉z坐标
- 把x 和y坐标都缩放到[-1, 1]区间
更简单的做法(实际做法):
- 将物体中心平移到原点
- 所有坐标缩放到[-1, 1] (称为标准立方体cuboid or canonical cube)
NOTES: x轴代表的是左右 y轴代表的是上下 z轴代表的是远近
所以按照坐标值来说 左<右,这样我们就能分清左右 下<上,这样我们就能分清上下 远<近,这样我们就能分清远近
值得一提的是,远近和我们直观上的区分是相反的。我们直观上以为越远距离越大,z坐标越大。实际上因为我们是沿着-z轴看去的,所以越远z坐标越小。
另外值得一提的是,OpenGL中则恰好相反,它规定看向z轴,于是越远z坐标越大,但是这样违背了右手系的规定。
于是我们按照这种做法,将一个x坐标范围[l, r] (left to right), y坐标范围[b, t] (bottom to top) ,z坐标范围[f, n] (far to near)的长方体正交投影到一个标准立方体
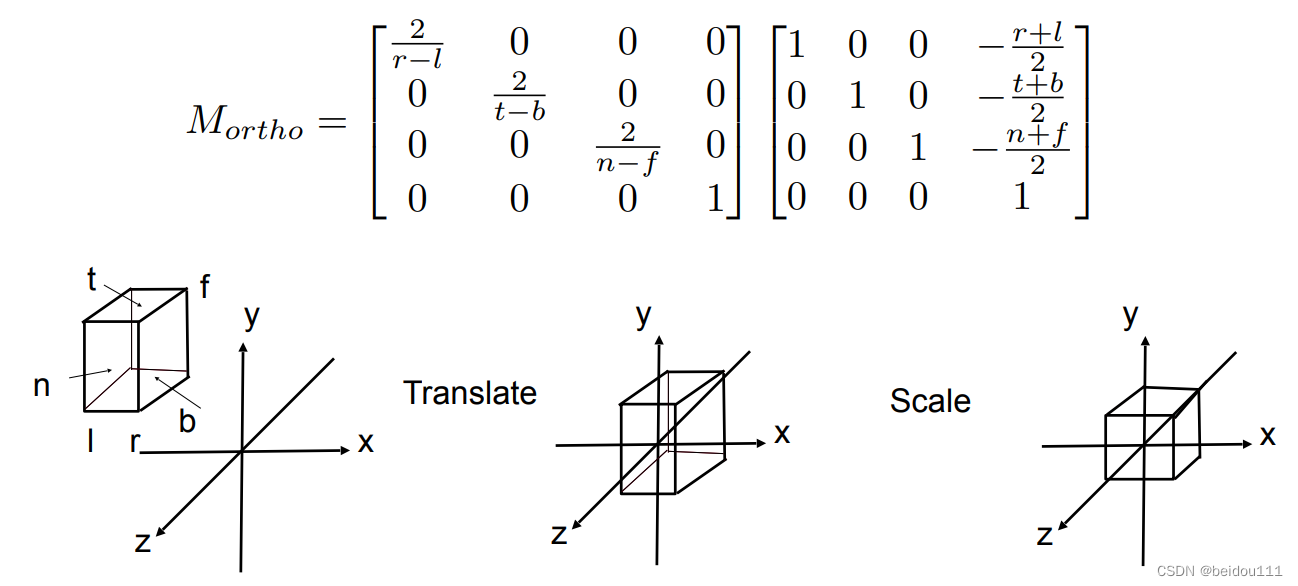
矩阵解释:从右向左乘。
右边的矩阵是平移矩阵:先找到中点,因此除以2,再平移。
左边的矩阵是缩放矩阵:因为缩放到[-1, 1], 因此缩放系数分子为2,分母就是原长度。
透视投影
在透视投影满足了近大远小的效果。原本的平行线投影后不一定平行。
我们要在一块固定大小的二维的屏幕上显示3D的物体,要呈现出近大远小的效果,于是就需要将透视投影转换为正交投影。然后再做正交投影,就得到了在2D固定大小屏幕上的显示。
关键是如何将透视投影转换为正交投影?
透视投影转换为正交投影
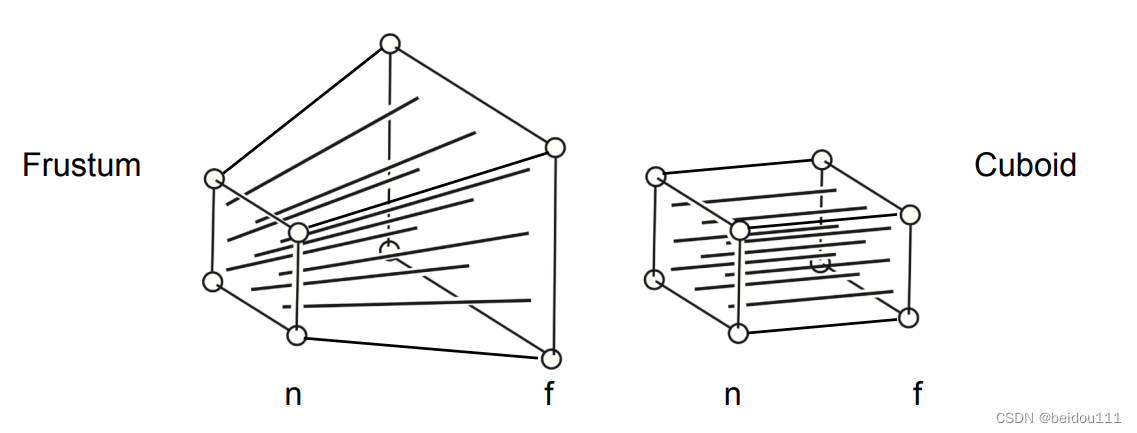
如图,就是要将左边的棱台挤压成右边的标准立方体。关键在于如何找到变换矩阵?
我们还是用待定系数法。
我们观察发现变换前后满足以下条件:
- 近平面和远平面上的z坐标不变
- 近平面n不做任何变换,即n平面上的任何点坐标不变
- 远平面的点虽然变换了,但其中心点坐标变换后与变换前完全一样
这里特别要注意第一条:只有远平面和近平面上的z坐标是不变的,其他平面是不满足这个条件的。
下面我们用这三个条件来待定系数。我们假设变换矩阵为M
于是变换写成
M
(
x
y
z
1
)
=
(
x
′
y
′
z
′
1
)
M\begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix}= \begin{pmatrix} x^\prime \\ y^\prime \\ z^\prime \\ 1 \end{pmatrix}
M⎝⎜⎜⎛xyz1⎠⎟⎟⎞=⎝⎜⎜⎛x′y′z′1⎠⎟⎟⎞
我们的目标就是根据待定系数法算出M
下面开始推导
取任意一条棱,例如最上边那条棱。可以构建出一个相似三角形
利用相似三角形,得到变换前后的坐标关系满足y ′ = n z y y'=\frac{n}{z} y y′=zny
同理得到 x ′ = n z x x'=\frac{n}{z} x x′=znx
将x’和y’带入进去,于是这个变换暂时可以写成
M ( x y z 1 ) = ( n x / z n y / z u n k o w n 1 ) M\begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix}= \begin{pmatrix} nx/z \\ ny/z \\ unkown \\ 1 \end{pmatrix} M⎝⎜⎜⎛xyz1⎠⎟⎟⎞=⎝⎜⎜⎛nx/zny/zunkown1⎠⎟⎟⎞
由于根据规定(见上节课),点的坐标值可以随意乘以一个系数,所以我们不妨同时乘以z,写成 M ( x y z 1 ) = ( n x n y u n k o w n z ) M\begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix}= \begin{pmatrix} nx \\ ny \\ unkown \\ z \end{pmatrix} M⎝⎜⎜⎛xyz1⎠⎟⎟⎞=⎝⎜⎜⎛nxnyunkownz⎠⎟⎟⎞M是一个4x4的矩阵,也就是我们要带求解的
我们观察到:
根据矩阵向量乘法,结果的每一个数都是矩阵的每一行乘以右侧向量。因此我们可以一行一行地待定求解矩阵 也就是把矩阵分解为 M = ( r ⃗ 1 r ⃗ 2 r ⃗ 3 r ⃗ 4 ) M=\begin{pmatrix} \vec r_1 \\ \vec r_2 \\ \vec r_3 \\ \vec r_4 \end{pmatrix} M=⎝⎜⎜⎛r1r2r3r4⎠⎟⎟⎞
因此第一行乘以(x y z 1) 得到 nx 第二行乘以(x y z 1) 得到 ny 第四行乘以(x y z 1) 得到 z
写成方程就是 r ⃗ 1 ⋅ ( x y z 1 ) = n x \vec r_1 \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} =nx r1⋅⎝⎜⎜⎛xyz1⎠⎟⎟⎞=nx
于是很容易就能求出来, r ⃗ 1 = ( n 0 0 0 ) \vec r_1= \begin{pmatrix} n & 0 & 0 &0 \end{pmatrix} r1=(n000)
同理, r ⃗ 2 = ( 0 n 0 0 ) \vec r_2=\begin{pmatrix} 0 & n & 0 &0 \end{pmatrix} r2=(0n00)
r ⃗ 4 = ( 0 0 1 0 ) \vec r_4 =\begin{pmatrix} 0 & 0 & 1 &0 \end{pmatrix} r4=(0010)
所以矩阵M就是 ( n 0 0 0 0 n 0 0 ? ? ? ? 0 0 1 0 ) \begin{pmatrix} n & 0 & 0 & 0\\ 0 & n & 0 &0 \\ ? & ? & ? &? \\ 0 & 0 & 1 &0 \end{pmatrix} ⎝⎜⎜⎛n0?00n?000?100?0⎠⎟⎟⎞
于是我们就只剩下第三行没有确定了。
如何确定第三行呢?
我们利用如下条件:
- 近平面上所有点的坐标不变
- 远平面上中心点的坐标不变
我们先说近平面。
假设近平面任意一点坐标为 ( x y n 1 ) \begin{pmatrix} x \\ y \\ n \\ 1 \end{pmatrix} ⎝⎜⎜⎛xyn1⎠⎟⎟⎞
这是假设了在该平面上的坐标为x y, 且z轴位于n(near)平面上,也就是远近距离为n。该点经过M的变换以后坐标不变,也就是
M ( x y n 1 ) = ( x y n 1 ) M\begin{pmatrix} x \\ y \\ n \\ 1 \end{pmatrix}= \begin{pmatrix} x \\ y \\ n \\ 1 \end{pmatrix} M⎝⎜⎜⎛xyn1⎠⎟⎟⎞=⎝⎜⎜⎛xyn1⎠⎟⎟⎞
但是这样做,M不就是单位阵了嘛?显然这样是没有意义的。但是利用同时乘以一个系数表示同一点的性质,我们可以把坐标同时乘以n。于是就写成 M ( x y n 1 ) = ( n x n y n 2 n ) M\begin{pmatrix} x \\ y \\ n \\ 1 \end{pmatrix}= \begin{pmatrix} nx \\ ny \\ n^2 \\ n \end{pmatrix} M⎝⎜⎜⎛xyn1⎠⎟⎟⎞=⎝⎜⎜⎛nxnyn2n⎠⎟⎟⎞
我们再次待定系数。这里就不写过程了。我们直接观察发现,第三行乘以n得到n^2。而这意味着:第三行把x和y给筛掉了。所以我们可以把第一个数和第二个数写为0。第三个数和第四个数仍然待定,记为A和B。
于是我们只剩下第三行最后两个数没有确定了。
同时,我们还能用上面的式子写出一个方程 A n + B = n 2 An+B=n^2 An+B=n2
然后再利用远平面中心点的那个条件。 远平面的中心点可以写为 ( 0 0 f 1 ) \begin{pmatrix} 0 \\ 0 \\ f \\ 1 \end{pmatrix} ⎝⎜⎜⎛00f1⎠⎟⎟⎞ 其中由于是中心点,所以x y坐标都是0。由于远近距离是f,所以第三个坐标是f
它经过变换以后,也是不变的。 M ( 0 0 f 1 ) = ( 0 0 f 1 ) M\begin{pmatrix} 0 \\ 0 \\ f \\ 1 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ f \\ 1 \end{pmatrix} M⎝⎜⎜⎛00f1⎠⎟⎟⎞=⎝⎜⎜⎛00f1⎠⎟⎟⎞
故技重施,将右端所有坐标同时乘以f M ( 0 0 f 1 ) = ( 0 0 f 2 f ) M\begin{pmatrix} 0 \\ 0 \\ f \\ 1 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ f^2 \\ f \end{pmatrix} M⎝⎜⎜⎛00f1⎠⎟⎟⎞=⎝⎜⎜⎛00f2f⎠⎟⎟⎞
于是我们就能写出第三行的另一个方程 ( 0 0 A B ) ( 0 0 f 1 ) = f 2 \begin{pmatrix} 0 & 0 & A & B \end{pmatrix}\begin{pmatrix} 0 \\ 0 \\ f \\ 1 \end{pmatrix}= f^2 \\ (00AB)⎝⎜⎜⎛00f1⎠⎟⎟⎞=f2
也就是
联立两个式子 A n + B = n 2 A f + B = f 2 An+B=n^2\\ Af+B=f^2 An+B=n2Af+B=f2 就能够解出A和B。
A = n + f B = − n f A=n+f\\ B=-nf A=n+fB=−nf
于是我们就解出来了整个M矩阵:
M = ( n 0 0 0 0 n 0 0 0 0 n + f − n f 0 0 1 0 ) M=\begin{pmatrix} n & 0 & 0 & 0\\ 0 & n & 0 &0 \\ 0 & 0 & n+f &-nf \\ 0 & 0 & 1 &0 \end{pmatrix} M=⎝⎜⎜⎛n0000n0000n+f100−nf0⎠⎟⎟⎞
推导到此结束。
接下来,只要再施加正交投影,就得到了3D到2D固定屏幕上的变换。本节课完。








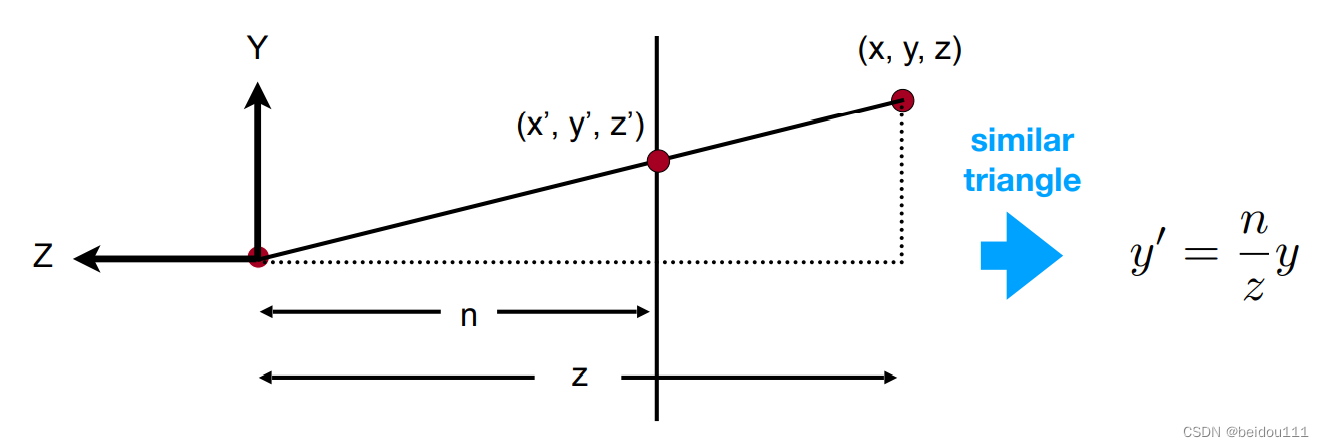
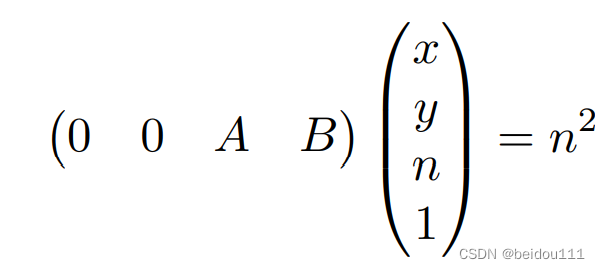













 1546
1546











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








