Rotation Representation 之 Axis-Angle & Rotation Matrix & Euler Angles & Quaternion & Rotation 6D

Axis-Angle

轴-角 / axis-angle 表示法
方便转换，几何意义明显
任何的旋转情况都归类为下面这种情况，
即一个旋转将向量 x 旋转为 x', 一定是绕一个旋转轴 n^旋转了 θ 度
因此，任何一个旋转都可以表示为一个旋转轴(x,y,z)和一个角度θ

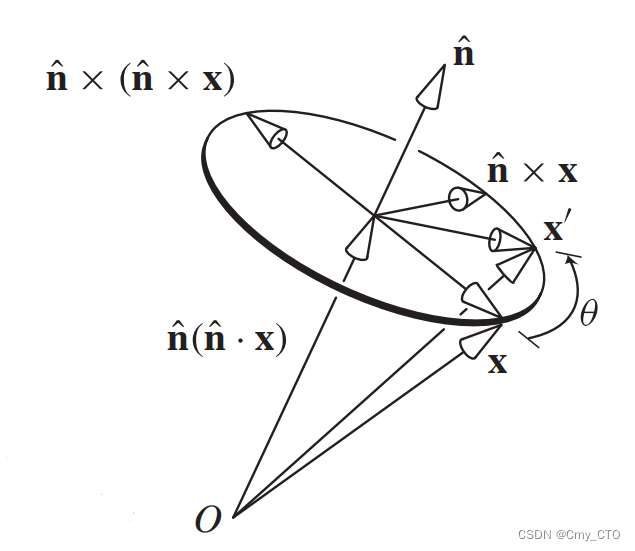
x Calc.

通过Rodrigues formula:

常见的写法Transform into:
通过叉乘矩阵和单位矩阵的一个减法

Euler Angles

Definition

欧拉角是由Leonhard Euler 提出的概念,用来描述刚体/移动坐标系在一个固定坐标系中的姿态.简单的说是使用XYZ三个轴的旋转分量,来描述一个6自由度的旋转.

欧拉角一般具有两大类表示方式,每类按照旋转次序的不同分为6小类:

Proper Euler angles (z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y)

Tait–Bryan angles (x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z).

每个大类都使用了3个变量描述三次旋转过程中的旋转角度, 差别在于Proper Euler angles只涉及两个转轴.而Tait–Bryan angles涉及三个转轴.一般在SLAM中我们使用的是Tait–Bryan angles.

Tait–Bryan angles 也被称为Cardan angles, nautical angles, (heading, elevation, and bank),(yaw, pitch, and roll). 我们接触的比较多的是yaw(偏航), pitch(俯仰), roll(横滚).三个变量一般对应(车体,飞行器的)z,y,x三个坐标轴.

Properties

一般对于旋转矩阵(33),旋转向量/角轴(31),四元数(4*1),给定一串数字,就能表示清楚一个姿态/旋转.
比如:
这里给出一个旋转矩阵R:

表示刚体在A某坐标系下的姿态, 我们就可以确切的画出刚体A的姿态.

但如果我给出一组欧拉角(后面都是指Tait–Bryan angles),绕x,y,z三个轴的转角分别为(α,β,γ),我们不能能确定一个明确的姿态.
需要再追加两个属性:
(1)旋转顺序
(2)内旋/外旋
才能确定的给出这组欧拉角对应的姿态.

Rotation Order

旋转顺序就是我们上文提到的Tait–Bryan angles (x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z).

我们指定绕x轴旋转α,绕y轴旋转β.但是可以有多个旋转顺序, 比如:

情况1:先绕x轴旋转α,再绕y轴旋转β.得到姿态 O1

情况2:先绕y轴旋转β,再绕x轴旋转α,得到姿态 O2

得到的 O1 一般是不等于 O2 的.

对于x,y,z三个轴的不同旋转顺序一共有(x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z)六种组合.
我们需要明确旋转顺序,才能确定欧拉角所指的姿态.

Intrinsic / Extrinsic rotations

等价的概念equipollent coextensive concept:

内旋(intrinsic rotations) = 旋转轴(rotated axis)

外旋(extrinsic rotations) = 固定轴(static/fixed axis)

内旋/外旋的定义

假设在世界坐标系中XYZ中存在物体,物体自身坐标系为xyz,假设初始状态物体相对XYZ的旋转为(0,0,0),即xyz与XYZ重合.
我们定义旋转顺序为z->y->x,转角分别为γ,β,α.

先绕z轴旋转γ,旋转过后,物体的x,y轴的坐标系发生了改变,z轴不变,得到新的物体自身坐标系 x2y2z ,此时的坐标轴 x2, y2 不再与世界坐标系的坐标轴XY重合.

内旋,外旋的区别

在转β(第二个转角)时:

内旋按照旋转后物体的坐标y轴,也就是 y2 旋转.

外旋按照世界坐标系中的Y轴旋转.

旋转最后一个角度时亦然.

因此, 增加了这两个概念(旋转顺序, 内外旋)后,我们描述一个能表示确定姿态/旋转的欧拉角,应该这样:

旋转角度(α,β,γ),旋转顺序(z->y->x),外旋.

或者:

旋转角度(α,β,γ),旋转顺序(x->y->z),内旋.

等等, 三个元素缺一不可.

Tips

旋转角度(α,β,γ),旋转顺序(x->y->z),内旋.

Essence

其实就是三个矩阵相乘

有动态定义和静态定义两种理解方法，

用动态定义理解为绕xyz轴分别旋转三个角度得到最后的图形，只不过要注意的是旋转的轴本身是会变的，但是矩阵乘法刚好也反映了这一点。

Code

以下所有代码表示的都是:

Python tf lib

from tf import transformations
import math
T = transformations.euler_matrix(x, y, z, "sxyz") 

numpy

import numpy as np
Rz = np.mat([[c1,-s1, 0],
[s1, c1, 0],
[0,0,1]])

Ry = np.mat([[c2, 0, s2],
[0, 1, 0],
[-s2, 0, c2]])

Rx = np.mat([[1,0, 0],
[0, c3, -s3],
[0,s3,c3]])

print(np.dot(Rz ,np.dot(Ry ,Rx)))

c++ eigen

#include <Eigen/Core>
#include <Eigen/Geometry>

Eigen::Matrix3d R = Eigen::AngleAxisd(euler[2], Eigen::Vector3d::UnitZ()) *
                    Eigen::AngleAxisd(euler[1], Eigen::Vector3d::UnitY()) * 
                    Eigen::AngleAxisd(euler[0], Eigen::Vector3d::UnitX());

Rotation Matrix

从代数的角度理解旋转矩阵，那就是空间之间的变换，同时，结合上面两种表示法，也可以有另外的理解。
首先是空间之间的变换。想象我们有两个三维线性空间的直角坐标系，一个u1^, u2^, u3^，一个 \hat{u_1}^',\hat{{u_1}‘},\hat{{u_1}^’} ，其中\hat{{u}^'}是u经过某种旋转变换得到的像，那么由线性代数的知识，在u1^, u2^, u3^坐标系下表示\hat{{u_1}^{'},\hat{{u_1}}‘},\hat{{u_1}^’}的坐标

将坐标写成矩阵，实际上就描述了这一旋转的矩阵：

轴-角表示的旋转可以写成rot(n^,θ),的形式，将叉乘矩阵带入上面的Rodrigues Formula，即可得到对应的矩阵形式。

Quaternion

Subconcept

空间中的子空间

一般而言，空间（维度>2）都存在更低维的子空间，比如二维空间中一维子空间，也就是直线；三维空间中的一维子空间和二维子空间，也就是直线和面。当超过三维的概念我们就很难去想象是什么样子，但四维空间一定会存在三维子空间或二维子空间。我们这里会加一个前缀超（hyper）来形容这些空间，比如高维空间中的平面我们称为超平面。

空间和子空间的映射

我们将二维空间表示为(x,y)，当y=0时，其实可以看成是一维的，只不过它表示成(x,0)这种形式。推到四维，(w,x,y,z)，当w=0时，(0,x,y,z)就是一个三维子空间，这也是为什么我们可以用单位四元数对三维向量进行操作，其实我们是将三维向量映射到四维的三维子空间（w=0，这种形式也成纯四元数），然后对其进行旋转，最终得到的向量结果依然是这个三维子空间中的，因而可以映射回三维空间。

广义球

这里的球是广义上的。我们在二维平面上，广义球其实指代circle，三维空间上就是我们认知上的球，称为two-sphere，而四维空间中广义球其实是一个超球（hyper-sphere），又称为three-sphere。单位向量其实就是广义球上面的点，而单位四元数也就是three-sphere上面的点。

约束与特征向量

空间中的一点由x, y, z等参数来表示，一般来说参数的数量与维数相等，二维空间的点用{x, y}参数，四维空间的点用{x, y, z, w}参数。但是对于空间的点加以约束，则该会减少参数的数量，比如三维空间的点在某一单位球面上，原本三个参数{x, y, z}才能表达的点现在只需要两个参数{u, v}就可以表达。如果{u, v}是单位向量，也可以称{u, v}是{x, y, z}的特征向量。

复数

为了满足数学家的强迫症，-1的平方根要有意义。看似很没有意义的复数，在实际中却用处非凡。我们首先看一下它的几何表达形式，令x为实部，y为虚部，则x+iy可以表示为下图。

复数的提出将原本一维的数值范围直接加了一个维度，数据量的增幅可以说是巨大的。那我们从极坐标的角度去思考复数，x+i·y可以写成r·cosθ+i·r·sinθ，我们只考虑单位复数，|r|=1，也就得到cosθ+i·sinθ。说到这，就要提一个代数学中常用的公式——欧拉公式，基本上复数的所有运算推到都会用到这个公式。

如何从复数推导出四元数，正如复数是有一个实部和一个虚部组成的，那我们将一个虚部换成三个虚部，即两两相交{i, j, k}。

其中n为三维的单位向量，i²=j²=k²=i·j·k=-1。这便是四元数的常规表达形式，不过单位四元数是有一大堆的约束的，并不是所有四维向量都是四元数。

这里再开一个脑洞，可能大家听说四元数、八元数，但是存在三元数、五元数？其实从客观上说，三元数、四元数、n元数都是存在的（也就是复数存在无穷个等级），但并不是所有的数系都满足模运算。而且随着维度的提高，特性会逐步牺牲，相比复数运算，四元数牺牲了交换律；相比四元数运算，八元数牺牲了结合律。当然也还存在十六元数，不过十六元数的特性将更少，在数学中也就更加没有意义，所以目前就四元数的应用最为广泛。

Definition & Characteristics

• 四元数（以后不特指四元数=单位四元数）是四维空间中一个超球上面的点，满足w²+x²+y²+z²=1；而纯四元数是四维空间在w=0时的一个子空间的点，形式为{0, q}特别注意的是纯四元数与四元数是不同的概念。
• 四元数是复数虚部扩展的结果，复数的虚部为1个，而四元数虚部有3个，且两两互相正交，其中实部是cosθ/2，而虚部为一个単位轴乘以sinθ/2。
• 四元数自由度并没有四个维度，由于存在w²+x²+y²+z²=1这个约束，它的自由度其实只有3，且每个四元数可以对应一个特征向量，即n。
  但请记住四元数并不是与特征向量一一对应的

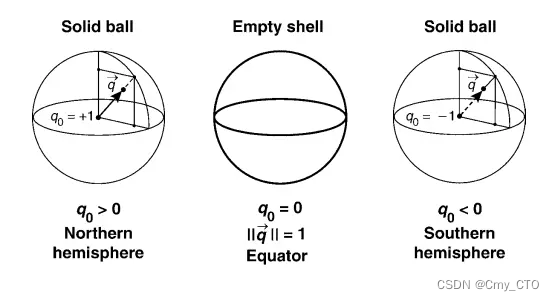
由于四元数存在于四维空间，所以如何利用低维信息去理解高维信息就显得尤为重要。我们这里先用三维举个例子，三维的球用代数表示为x²+y²+z²=1，虽然球上面的点是由x，y，z三个参数来确定，但实际上我们只需要两个。假设取x和z表示，其中y可以通过x和z进行求解。那么，我们将y轴信息给隐去，只看投影平面，如下图所示。这张图的意思是，整个球在XOZ平面上投影是一个圆，当球面一点投影在圆上时，y=0；投影的位置位于圆内时，则分别两种情况，y>0处于北半球，y<0处于南半球。所以我们仅通过投影后的圆即可还原出整个球体。

推广到四维，w²+x²+y²+z²=1中取x、y和z来表示超球。如下图所示，四维空间投影到三维超平面（w=0）可能是一个two-sphere。当投影点在整个two-sphere的边缘时，w一定为0，值得一提的是在这个空间内的四元数是一个纯四元数。当投影点落在two-sphere的内部时，也分为两种情况，w>0和w<0。但是我们可以发现这两种情况下对应的特征向量是一样的，所以我们将旋转矩阵向四元数转换时，是有两个对应值的，四元数的范围是2倍覆盖于3D旋转（2:1 mapping）。

Quaternion Multiply

四元数之间的“乘法”规则是满足群的性质
由于四元数有i，j，k三个虚部，所以得满足i²=j²=k²=i·j·k=-1这个条件。这里令★为“乘法”操作符，则p★q的公式如下

对单位四元数，按照群的性质一条条过：

• 封闭性：易证明，p和p的共轭相乘即可，|p★q|=1。
• 结合律：这条也很好证明，只要证明(p★q)★r=p★(q★r)。

由于单位四元数旋转后还是单位四元数，所以满足封闭性。同时，类比矩阵乘法，单位四元数也应该满足结合律。

• 单位元素：e=(1,0,0,0)，这也是四元数的一个初始值（相当于单位矩阵）。带入上面的公式可知，p★(1,0,0,0)还是等于p。
• 逆元素：p存在一单位四元数，★操作的结果为e，具体参考下面公式，可以看出逆元素就是其共轭除以模的平方。
  
  如果这里是复数，可能还会满足交换律，就是一个阿贝尔群。但四元数肯定不满足交换律，无论从代数的角度，还是从几何角度。

Exponents & Logarithms & Inner Products

指数、对数与内积

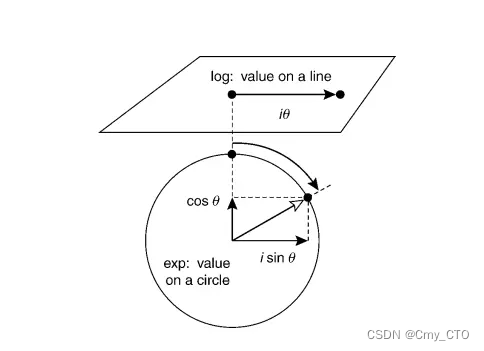
Quaternion Exponents 指数

根据欧拉公式可知，四元数的指数形式只是换了一种表达方式，都是表达同一个东西。而其对数形式也就是四元数指数形式的指数，如下图公式所示。这对公式在计算四元数插值的时候很有用

Quaternion Logarithms 对数

其实对数的变化量其实就是角度的大小，所以用下图可以很直观的看出四元数指数形式和对数形式之间的关系。

Quaternion Inner Products 内积

我们先看三维空间或二维空间，如果两个单位向量算内积，内积的结果为两个向量的夹角。四元数也是如此，两个单位四元数的内积就是其夹角，这个结论推广到n维也是成立，原因很简单，因为三点共面，即使n维空间，两个向量所在的空间也仅是二维子空间。

至于外积，由于对于复数和四元数来说，外积的意义均不是很明显，这里就不做过多讨论。

Rotation 6D

比较了旋转矩阵，欧拉角，四元数等常见三维旋转表示对神经网络训练的影响，并提出了一种适合深度学习的 6D三维旋转表示方法。

6D是指6个自由度，代表了3个自由度的位移 (也叫平移(Translation))，以及3个自由度的空间旋转(Rotation)，合起来就叫位姿(Pose)。 位姿是一个相对的概念，指的是两个坐标系之间的位移和旋转变换。

Rotation Matrix to Rotation 6D

Code

def matrix_to_rotation_6d(matrix: torch.Tensor) -> torch.Tensor:
    """
    Converts rotation matrices to 6D rotation representation by Zhou et al. [1]
    by dropping the last row. Note that 6D representation is not unique.
    Args:
        matrix: batch of rotation matrices of size (*, 3, 3)

    Returns:
        6D rotation representation, of size (*, 6)

    [1] Zhou, Y., Barnes, C., Lu, J., Yang, J., & Li, H.
    On the Continuity of Rotation Representations in Neural Networks.
    IEEE Conference on Computer Vision and Pattern Recognition, 2019.
    Retrieved from http://arxiv.org/abs/1812.07035
    """
    return matrix[..., :2, :].clone().reshape(*matrix.size()[:-2], 6)

Rotation 6D to Rotation Matrix

施密特正交化

Code

def rotation_6d_to_matrix(d6: torch.Tensor) -> torch.Tensor:
    """
    Converts 6D rotation representation by Zhou et al. [1] to rotation matrix
    using Gram--Schmidt orthogonalization per Section B of [1].
    Args:
        d6: 6D rotation representation, of size (*, 6)

    Returns:
        batch of rotation matrices of size (*, 3, 3)

    [1] Zhou, Y., Barnes, C., Lu, J., Yang, J., & Li, H.
    On the Continuity of Rotation Representations in Neural Networks.
    IEEE Conference on Computer Vision and Pattern Recognition, 2019.
    Retrieved from http://arxiv.org/abs/1812.07035
    """

    a1, a2 = d6[..., :3], d6[..., 3:]
    b1 = F.normalize(a1, dim=-1)
    b2 = a2 - (b1 * a2).sum(-1, keepdim=True) * b1#归一化后b1内积为1，表达式中省去
    b2 = F.normalize(b2, dim=-1)
    b3 = torch.cross(b1, b2, dim=-1)#第三个正交向量垂直前两个正交向量所在的面（叉乘）
    return torch.stack((b1, b2, b3), dim=-2)

Visualization

Code

# Copyright (c) Facebook, Inc. and its affiliates.
# All rights reserved.
#
# This source code is licensed under the BSD-style license found in the
# LICENSE file in the root directory of this source tree.

import functools
from typing import Optional
import torch
import torch.nn.functional as F

"""
The transformation matrices returned from the functions in this file assume
the points on which the transformation will be applied are column vectors.
i.e. the R matrix is structured as

    R = [
            [Rxx, Rxy, Rxz],
            [Ryx, Ryy, Ryz],
            [Rzx, Rzy, Rzz],
        ]  # (3, 3)

This matrix can be applied to column vectors by post multiplication
by the points e.g.

    points = [[0], [1], [2]]  # (3 x 1) xyz coordinates of a point
    transformed_points = R * points

To apply the same matrix to points which are row vectors, the R matrix
can be transposed and pre multiplied by the points:

e.g.
    points = [[0, 1, 2]]  # (1 x 3) xyz coordinates of a point
    transformed_points = points * R.transpose(1, 0)
"""


def rotation_6d_to_matrix(d6: torch.Tensor) -> torch.Tensor:
    """
    Converts 6D rotation representation by Zhou et al. [1] to rotation matrix
    using Gram--Schmidt orthogonalization per Section B of [1].
    Args:
        d6: 6D rotation representation, of size (*, 6)

    Returns:
        batch of rotation matrices of size (*, 3, 3)

    [1] Zhou, Y., Barnes, C., Lu, J., Yang, J., & Li, H.
    On the Continuity of Rotation Representations in Neural Networks.
    IEEE Conference on Computer Vision and Pattern Recognition, 2019.
    Retrieved from http://arxiv.org/abs/1812.07035
    """

    a1, a2 = d6[..., :3], d6[..., 3:]
    b1 = F.normalize(a1, dim=-1)
    b2 = a2 - (b1 * a2).sum(-1, keepdim=True) * b1
    b2 = F.normalize(b2, dim=-1)
    b3 = torch.cross(b1, b2, dim=-1)
    return torch.stack((b1, b2, b3), dim=-2)


def matrix_to_rotation_6d(matrix: torch.Tensor) -> torch.Tensor:
    """
    Converts rotation matrices to 6D rotation representation by Zhou et al. [1]
    by dropping the last row. Note that 6D representation is not unique.
    Args:
        matrix: batch of rotation matrices of size (*, 3, 3)

    Returns:
        6D rotation representation, of size (*, 6)

    [1] Zhou, Y., Barnes, C., Lu, J., Yang, J., & Li, H.
    On the Continuity of Rotation Representations in Neural Networks.
    IEEE Conference on Computer Vision and Pattern Recognition, 2019.
    Retrieved from http://arxiv.org/abs/1812.07035
    """
    return matrix[..., :2, :].clone().reshape(*matrix.size()[:-2], 6)

import math
import numpy as np
from torch.nn import functional as F

# 初始化一个旋转角度
angle = 90/180*math.pi
# 创建一个三维坐标变换矩阵
transform_matrix_z = np.array([
        [math.cos(angle), -math.sin(angle), 0],
        [math.sin(angle), math.cos(angle), 0],
        [0, 0, 1]])#绕z轴

transform_matrix_x = np.array([
        [1, 0, 0],
        [0, math.cos(angle), -math.sin(angle)],
        [0, math.sin(angle), math.cos(angle)]])#绕x轴

transform_matrix_y = np.array([
        [math.cos(angle), 0, math.sin(angle)],
        [0, 1, 0],
        [-math.sin(angle), 0, math.cos(angle)]])#绕y轴

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


fig = plt.figure(figsize=(10, 8))
ax = Axes3D(fig)

ax.scatter3D(0,0,0,s=5)
ax.text3D(0,0,0,"(0,0,0)")
ax.text3D(5,0,0,"X")
ax.text3D(0,5,0,"Y")
ax.text3D(0,0,5,"Z")
ax.plot3D([0,5], [0,0], [0,0], marker='>', linewidth=2)
ax.plot3D([0,0], [0,5], [0,0], marker='>', linewidth=2)
ax.plot3D([0,0], [0,0], [0,5], marker='>', linewidth=2)

z = np.linspace(0, 4, 200)
x = z * np.sin(20 * z)
y = z * np.cos(20 * z)
A = np.array([list(x), list(y), list(z)])
'''旋转方向'''
R = transform_matrix_x
R_ = np.array(rotation_6d_to_matrix(matrix_to_rotation_6d(torch.tensor(R))))
print("R", R)
print("R_", R_)

A1 = np.matmul(R_, A)
ax.plot3D(A[0], A[1], A[2], marker='o')
ax.plot3D(A1[0], A1[1], A1[2], marker='>', linewidth=2)

plt.rcParams.update({'font.family': 'Times New Roman'})
plt.rcParams.update({'font.weight': 'normal'})
plt.rcParams.update({'font.size': 20})
# Tweaking display region and labels
# ax.set_xlim(-5, 5)
# ax.set_ylim(-5, 5)
# ax.set_zlim(-5, 5)
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')

plt.show()

Reference

[1] https://en.wikipedia.org/wiki/Euler_angles

[2] https://en.wikipedia.org/wiki/Axis%E2%80%93angle_representation

[3] https://en.wikipedia.org/wiki/Quaternion

[4] https://zhuanlan.zhihu.com/p/85108850

[5]https://openaccess.thecvf.com/content_CVPR_2019/html/Zhou_On_the_Continuity_of_Rotation_Representations_in_Neural_Networks_CVPR_2019_paper.html