👨🎓个人主页
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
无迹卡尔曼滤波(UKF)在FitzHugh-Nagumo神经元动力学研究中的应用
💥1 概述
无迹卡尔曼滤波(UKF)在FitzHugh-Nagumo神经元动力学研究中的应用
本文综述了连续非线性动力系统噪声时间序列测量中参数和未观测到的轨迹分量的估计问题。首先表明,在没有明确考虑测量误差的参数估计技术(如回归方法)中,噪声测量会产生不准确的参数估计。另一个问题是,对于混沌系统,必须最小化以估计状态和参数的成本函数非常复杂,以至于常见的优化例程可能会失败。我们表明,包含有关潜在轨迹的时间连续性的信息可以显着改善参数估计。本文详细描述了两种同时考虑变量误差问题和复杂成本函数问题的方法:射击方法和递归估计技术。两者都在数值示例中进行了演示。
一、FitzHugh-Nagumo神经元动力学模型概述
FitzHugh-Nagumo(FHN)模型是Hodgkin-Huxley模型的简化版本,通过两个耦合的非线性微分方程描述神经元的电活动特性。其核心数学表达式为:

其中:
- V为膜电位(快变量),反映动作电位的快速变化;
- W为恢复变量(慢变量),描述钠/钾通道的慢速恢复过程;
- Iext为外部刺激电流,τ,a,b为模型参数。
该模型在分岔分析中表现出丰富的动力学行为,例如当外部电流IextIext超过阈值时,系统会通过Hopf分岔从静息态转为周期性放电。分数阶FHN模型(通过Caputo导数引入分数阶qq)进一步扩展了整数阶模型,分析表明分数阶模型具有更宽的稳定域和更高的放电频率。
二、无迹卡尔曼滤波(UKF)的核心原理
UKF是一种基于无迹变换(Unscented Transform, UT)的非线性滤波算法,其核心是通过确定性采样(Sigma点)逼近非线性系统的统计特性,避免了扩展卡尔曼滤波(EKF)的线性化误差。具体步骤如下:
- Sigma点生成:根据状态均值和协方差矩阵生成2n+12n+1个Sigma点(nn为状态变量维度),确保其均值和协方差与原分布一致。
- 预测步骤:将Sigma点通过非线性状态方程传播,计算预测状态均值和协方差。
- 更新步骤:利用观测方程计算预测测量值,结合实际观测数据更新卡尔曼增益,最终修正状态估计和协方差。
UKF的优势在于:
- 高阶精度:对非线性函数的统计量估计精度可达二阶或更高,优于EKF的一阶近似;
- 无需雅可比矩阵:适用于不可导或强非线性系统;
- 计算效率:复杂度与EKF相当,适合实时应用。
三、UKF在FHN模型中的状态估计框架
1. 状态变量与观测方程
-
状态变量:通常选择x=[V,W]T,即膜电位和恢复变量。
-
观测方程:假设仅能测量含噪声的膜电位,则观测方程为:

其中vk为高斯白噪声,协方差为RR。
2. 应用场景
UKF在FHN模型中的典型应用包括:
- 状态估计:从噪声观测中恢复真实的膜电位和恢复变量轨迹;
- 参数辨识:联合估计模型参数(如a,b,τa,b,τ)和状态变量;
- 噪声抑制:在神经信号采集设备中滤除环境噪声,提高信号质量。
四、现有文献中的具体应用案例
- 状态估计与参数辨识:
- Voss等人(2004)首次将UKF应用于FHN模型,通过含噪声的膜电位观测数据成功重构了恢复变量和外部电流参数。
- 自适应UKF(RAUKF)被用于Morris-Lecar神经元模型,在参数突变或测量故障时仍保持鲁棒性。
- 仿真实验验证:
- Matlab仿真显示,UKF在FHN模型中的状态估计误差(RMSE)显著低于EKF,尤其在强非线性区域(如动作电位峰值)表现更优。
- 针对分数阶FHN模型,UKF能够有效处理分数阶导数引入的非局部效应。
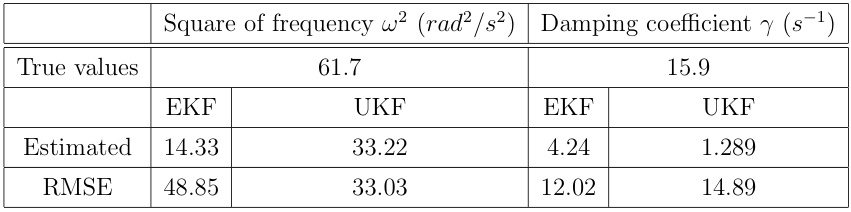
五、UKF性能评估指标
在FHN模型中,滤波性能可通过以下指标量化:
-
均方根误差(RMSE):

用于评估状态估计值与真实值的偏差。
-
参数估计误差:
比较估计参数a^,b^a^,b^与真实值的相对误差,验证辨识精度。 -
收敛速度:
分析状态估计误差随迭代次数的衰减速率,反映算法对初始条件的敏感性。 -
协方差矩阵迹:
协方差矩阵的迹(Trace)反映估计的不确定性,理想情况下应随时间收敛。
六、挑战与未来方向
- 复杂噪声环境:FHN神经元常受非高斯噪声(如双色噪声)干扰,需结合自适应UKF或混合滤波方法。
- 实时性优化:针对大规模神经网络仿真,需开发并行化UKF算法以降低计算负载。
- 临床结合:将UKF估计结果用于闭环神经调控(如深脑刺激),需解决生物信号采集的延迟与非线性问题。
总结
UKF凭借其非线性处理能力和计算效率,为FHN神经元动力学的状态估计提供了高精度解决方案。现有研究已验证其在噪声抑制、参数辨识和分岔分析中的有效性,未来可通过结合自适应机制和硬件加速进一步拓展其应用场景。
📚2 运行结果

部分代码:
% Simulating data: %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
x0=zeros(2,ll); x0(:,1)=[0; 0]; % true trajectory
dt=.1*dT; nn=fix(dT/dt); % the integration time step is smaller than dT
% External input, estimated as parameter p later on:
z=(1:ll)/250*2*pi; z=-.4-1.01*abs(sin(z/2));
% 4th order Runge-Kutta integrator for FitzHugh-Nagumo system with external input:
for n=1:ll-1;
xx=x0(:,n);
for i=1:nn
k1=dt*FitzHughNagumo_int(xx,z(n));
k2=dt*FitzHughNagumo_int(xx+k1/2,z(n));
k3=dt*FitzHughNagumo_int(xx+k2/2,z(n));
k4=dt*FitzHughNagumo_int(xx+k3,z(n));
xx=xx+k1/6+k2/3+k3/3+k4/6;
end;
x0(:,n+1)=xx;
end;
x=[z; x0]; % augmented state vector (notation a bit different to paper)
R=.2^2*var(FitzHughNagumo_obsfct(x))*eye(dy,dy); % observation noise covariance matrix
rng('default'); rng(0)
y=FitzHughNagumo_obsfct(x)+sqrtm(R)*randn(dy,ll); % noisy data
FitzHughNagumo_fct(dq,x); % this is just to suppress an erroneous warning and otherwise has no function
% Initial conditions %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
xhat=zeros(dx,ll);
xhat(:,2)=x(:,2); % first guess of x_1 set to observation
Q=.015; % process noise covariance matrix
Pxx=zeros(dx,dx,ll);
Pxx(:,:,1)=blkdiag(Q,R,R);
errors=zeros(dx,ll);
Ks=zeros(dx,dy,ll); % Kalman gains
% Main loop for recursive estimation %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for k=2:ll
[xhat(:,k),Pxx(:,:,k),Ks(:,:,k)]=ut(xhat(:,k-1),Pxx(:,:,k-1),y(:,k),'FitzHughNagumo_fct','FitzHughNagumo_obsfct',dq,dx,dy,R);
Pxx(1,1,k)=Q;
errors(:,k)=sqrt(diag(Pxx(:,:,k)));
end; % k
% Results %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
chisq=mean((x(1,:)-xhat(1,:)).^2+(x(2,:)-xhat(2,:)).^2+(x(3,:)-xhat(3,:)).^2);
disp(['Chi square = ',num2str(chisq)]);
% Showing last estimated parameter, used for example for the final estimate of a constant parameter:
% est=xhat(1:dq,ll)'; disp(['Estimated x = ' num2str(est)]);
% error=errors(1:dq,ll)'; disp(['Error = ' num2str(error)]);
figure(1)
subplot(2,1,1)
plot(y,'bd','MarkerEdgeColor','blue', 'MarkerFaceColor','blue','MarkerSize',3);
hold on;
plot(x(dq+1,:),'black','LineWidth',2);
%plot(xhat(dq+1,:),'r','LineWidth',2);
xlabel(texlabel('t'));
ylabel(texlabel('x_1, y'));
hold off;
axis tight
title('(a)')
drawnow
subplot(2,1,2)
plot(x(dq+2,:),'black','LineWidth',2);
hold on
plot(xhat(dq+2,:),'r','LineWidth',2);
plot(x(1,:),'black','LineWidth',2);
for i=1:dq; plot(xhat(i,:),'m','LineWidth',2); end;
for i=1:dq; plot(xhat(i,:)+errors(i,:),'m'); end;
for i=1:dq; plot(xhat(i,:)-errors(i,:),'m'); end;
xlabel(texlabel('t'));
ylabel(texlabel('z, estimated z, x_2, estimated x_2'));
hold off
axis tight
title('(b)')
function r=FitzHughNagumo_int(x,z)
% Function for modeling data, not for UKF execution
a=.7; b=.8; c=3.;
r=[c*(x(2)+x(1)-x(1)^3/3+z); -(x(1)-a+b*x(2))/c];
function r=FitzHughNagumo_obsfct(x)
% Observation function G(x)
k1=dt*fc(xnl,p);
k2=dt*fc(xnl+k1/2,p);
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1] Voss H U , Timmer J , Kurths J .NONLINEAR DYNAMICAL SYSTEM IDENTIFICATION FROM UNCERTAIN AND INDIRECT MEASUREMENTS[J].International Journal of Bifurcation and Chaos, 2011, 14(6):1905-1905.DOI:10.1142/S0218127404010345.

























 1021
1021

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










