GNN理论基础：空间域的卷积理论（待更新）

一、参考文献：

Zhewei Wei's Homepage 魏哲巍 (weizhewei.com)

平凡的久月的个人空间-平凡的久月个人主页-哔哩哔哩视频 (bilibili.com)

ShiChuan @ BUPT

图邻接矩阵、训练数据的标准化及批归一化的原则_邻接矩阵归一化-CSDN博客

图嵌入（Graph embedding）- 简介 - 知乎 (zhihu.com)

二、从卷积神经网络到图结构数据序列：

        1.欧氏空间数据与非欧式空间数据：

        1.1欧氏空间数据：

        欧氏空间是对现实空间的规则抽象与推广（从n≤3推广到有限n维空间），在欧几里得几何中，平行线任何位置的间距相等。在中学中学到的余弦值、点间的距离都是在低纬空间（二维空间）中，如果将低维空间所总结的规律推广到n维空间（正弦、余弦等），这些符合定义的空间则被称为欧氏空间。

        再让我们回顾一下概念，在百度百科的定义中“设V是实数域R上的线性空间，如果V上存在定义着正定对称双线性g，则称V是欧几里得空间。”正定对称双线性g满足以下性质。①对称性：②分配律：③始终在曲线之上：且当且仅当的时候成立。

        内积指的是两个向量的乘积，也就是两个向量的长度称两个向量间的余弦角，如果是两个数列的向量相乘，则是这一系列数列内的向量的乘积再加和。

        1.2非欧氏空间数据：

        非欧式几何是指不同于欧几里得几何学的几何体系，简称非欧几何，一般指的是罗巴切夫斯基几何和黎曼几何的椭圆几何。黎曼空间是一种非欧几里得空间，是一种弯曲空间，具有不变的线元ds2=gikdxidxk，其中，作为广义坐标(x0,x1,...xn)，称为黎曼度规。

        通俗的讲，如果空间有四维，而我们生活在三维空间中，而这个三维空间再空间的第四个维度中发生了弯曲，我们的几何必须修正。也就是说对感知不到的维度进行修正的空间被称为非欧式空间数据。

        2.图结构数据序列的无序性：

        3.图的定义以及归一化拉普拉斯矩阵的计算：

          3.1  图的定义：

            一个图可以形式定义为一个二元组：，其中是顶点（结点）的有穷集合。是边集，连接中顶点集合中的顶点的边的集合。如果中的顶点对是有序的，即中的每一条边都是有方向的，则称为有向图。如果边集没有方向则称是无向图。

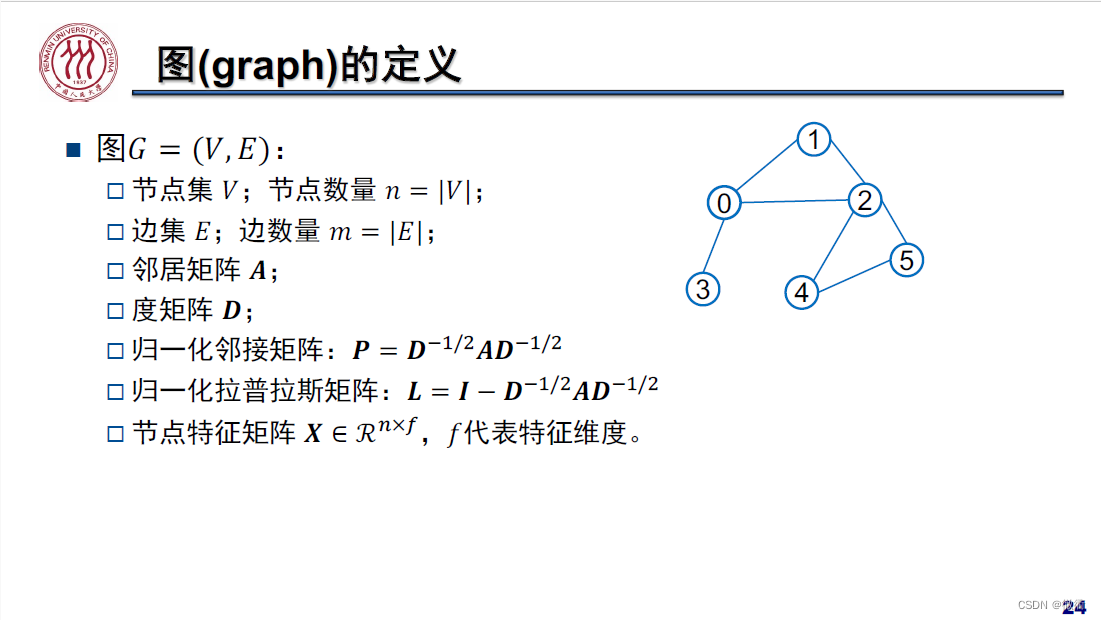
           有向图相较于无向图能带来更多的信息，比如知识图谱中的有向边可以确定父项和子项，无项图可以将节点的边视为节点与节点之间存在两个有向边（例如在下图中节点1和节点0存在两个方向相反的边，发生抵消，故为无向图）

           如果下面这个图是一个有向图，则可以描述为,其中顶点集合{}，边集合为{}。

        3.2 拉普拉斯矩阵的计算方法以及有向图和矩阵之间的转化：

        拉普拉斯矩阵的定义：给定一个具有n个顶点的简单图 = ,为顶点集合，为边集合，其拉普拉斯矩阵的定义为。其中∈为邻接矩阵，∈为度矩阵。邻接矩阵的元素为0和1，其对角线元素全为0。度矩阵是一个对角矩阵，对角线上元素的计算值为。

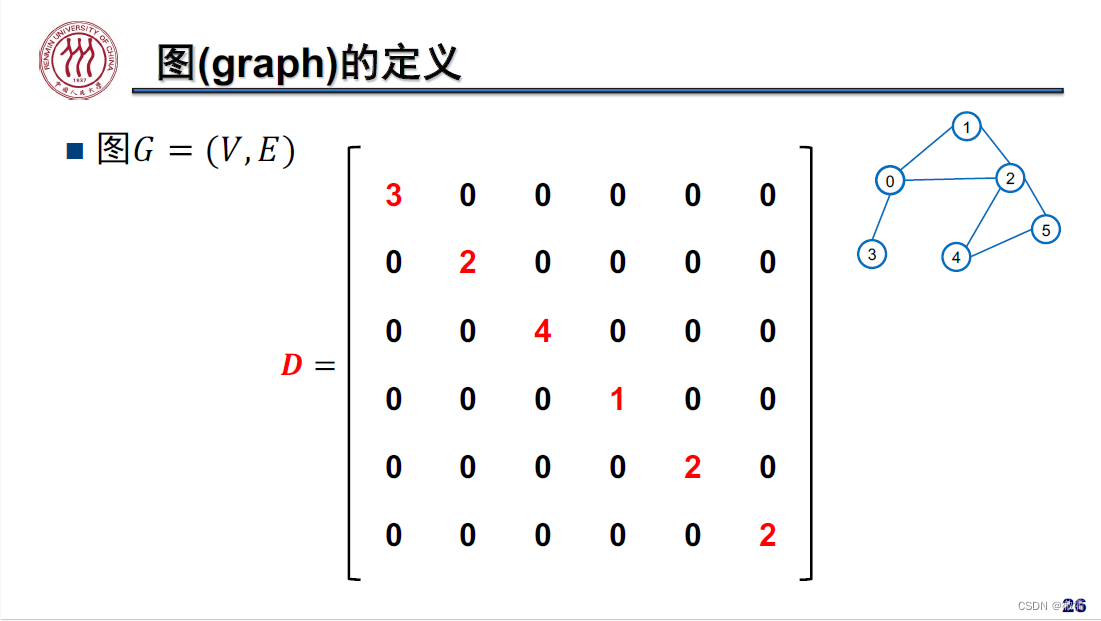
        我们对上面这个有向图转化为邻接矩阵和度矩阵，矩阵的宽和高分别代表着顶点,如果顶点和顶点存在有向边，则度矩阵为1。

        在求解上面有向图的接邻矩阵， 对每一列存在的有向边的数量进行加和，可以得到存在有向边的数量。如果使用邻接表，可以减少计算机的存储，提高计算速度。（,,）

        3.3归一化邻接矩阵以及归一化拉普拉斯矩阵：

        为了能够使拉普拉斯举证的对角上的元素全部为1便于计算，我们通过设计归一化邻接矩阵和归一化拉普拉斯矩阵。归一化邻接矩阵是邻接矩阵和度矩阵的逆矩阵得到。

         使用对角为1的矩阵减去归一化邻接矩阵即可得到归一化拉普拉斯矩阵。

        4.图嵌入（Graph embedding）的基本理论 ：

            4.1使用图嵌入的原因： 

             计算机图形是有限的，图由边和节点组成。这些网络关系只能使用数学、统计和机器学习的特定子集，而向量空间有更丰富的方法工具集。使用邻接矩阵作为大型图的特征空间，会大大增加计算成本，使用嵌入矩阵相较于邻接矩阵更加实用，嵌入矩阵可以将节点属性打包到一个维度更小的向量中。运算更快，运算成本更低。

            4.2图嵌入的概念：

             图嵌入是一种将图数据（高维稠密的矩阵）映射为低纬稠密向量的过程，能够很好地解决图数据难以高效地输入机器学习算法地问题。图嵌入应该捕获图的拓扑结构、顶点到顶点的关系以及关于图、子图和顶点的其他相关信息。

              可以将常见的嵌入式方法分为以下两类：①顶点嵌入：每个顶点用其自身的向量表示进行编码。这种嵌入一般用于在顶点层次上执行可视化或者预测。比如在2D平面上显示顶点，或者居于顶点相似性预测新的连接。②图嵌入：用单个向量表示整个图，这种嵌入用于在图的层次上做出预测，常用于比较化学结构。

        5.顶点嵌入方法：

        顶点嵌入的方法可以分为三大类:因式分解方法、随机游走方法和深度方法。DeepWalk使用随机漫步来生成嵌入，随机游走从一个选定的节点开始，然后我们从一个当前节点移动到随机邻居节点，移动一定数量的步。主要步骤可以分为以下三步：①抽样：用随机游动抽样一个图，作者证明了从每个节点执行32到64游走是足够的，一般良好的随机漫步的长度约为40步。②训练