【PID控制】几种调参方法的比较 (含计算代码)

摸鱼摸鱼疯狂摸鱼

已于 2023-06-27 11:11:40 修改

阅读量4.9k

点赞数 11

分类专栏： PID控制文章标签：笔记

于 2023-06-27 10:51:29 首次发布

本文链接：https://blog.csdn.net/weixin_64530445/article/details/131409616

版权

PID控制专栏收录该内容

2 篇文章 3 订阅

订阅专栏

⭐⭐几种整定方法总结(含参数计算代码)⭐⭐

PID 参数整定方法

临界比例度法 (Ziegle-Nichols算法齐格勒尼科尔斯整定方法)

适用条件

主要原理

PID控制器类型的选择

开环阶跃响应曲线整定 (有Z-N和C-C两套经验公式)

⭐⭐几种整定方法总结(含参数计算代码)⭐⭐

临界振荡调参法是不好用的，很难调到所需的位置；
对于一阶延时系统(弧型阶跃响应)，几种方案优先级：P-V法 > IMC法 > 阶跃响应C-C/Z-N法(会出现明显振荡)
对于一阶无延时系统，可以构造一个d，使用上述方法，其中 阶跃响应C-C/Z-N法最优
对于二阶延时系统，时间常数大、时滞比大时使用IMC法优于等效阶跃响应法(更快，超调相似，简便)
对于更高阶的系统(S型阶跃响应)使用等效阶跃响应法(用一阶延时模拟，再查表选取Z-N/C-C法)可以实现控制

（斜率最大点作切线，以切点的横坐标作为时滞d，切点与后点的时间间隔为时间常数 $\tau_M$ ）

适用性（选择优先级从高到低分别为：绿色 > 黄色 > 红色）：

代码整合：

%%系统已知   或已经被等效过（高阶时滞(等效)阶跃响应曲线法
%%---------------------一阶时滞 优先选择P-V法-灵敏度峰值1.4 PI控制-----------------------------------------
%%---------------------开环阶跃响应图像参数
d = ;tau = ;Kss = ;%%注意simulink中控制器要选用理想型(不用并行)
%%---------------------P-V   PI控制  灵敏度峰值为1.4
K1_pv=(0.2958*(d/(d+tau))^(-1.014)-0.2021)/Kss;I1_pv=1/tau/(1.624*(d/tau)^0.2269-0.5556);
K=K1_pv
I=I1_pv
%%---------------------二阶时滞 时滞比大(tau大)时 IMC法 快速性更好--------------------------------
%%---------------------开环阶跃响应图像参数
d = ;Kss = ;epsi = ;tau1 = ;tau2 = ;%%注意simulink中控制器要选用理想型(不用并行)  一般可取epsi=0
K2_imc=tau1/Kss/(epsi+d);I2_imc=1/min(tau1,4*(epsi+d));D2_imc=tau2;
K=K2_imc
I=I2_imc
D=D2_imc
%%--------------------一阶无时滞时  阶跃响应曲线法-------------------------------  
%%系统未知，需要等效
%%---------------Z-N法/C-C法    具体用哪种可以查表-------------------------------
%%---------------------开环阶跃响应图像的参数--------------------------
d = ;tau = ;Kss = ;%%d是滞后时间、tau为时间常数
%%---------------------注意simulink中控制器要选用理想型(不用并行)
%%---------------------Z-N法-----------------------------------------------------
K1_zn=tau/Kss/d;
K2_zn=tau/Kss/d*0.9;I2_zn=1/3/d;
K3_zn=tau/Kss/d*1.2;I3_zn=1/2/d;D3_zn=0.5*d;
%%---------------------Cohen-Coon法-----------------------------------------------
K1_cc=tau/Kss/d*(1+d/3/tau);
K2_cc=tau/Kss/d*(0.9+d/12/tau);I2_cc=1/(d*(20*tau+3*d)/(9*tau+20*d));
K3_cc=tau/Kss/d*(4/3+d/4/tau);I3_cc=1/(d*(32*tau+6*d)/(13*tau+8*d));D3_cc=4*d*tau/(11*tau+2*d);

基本都需要依靠系统的阶跃响应曲线、读取时滞等参数、进行PID参数整定。

下文中详细介绍各种方法的适用条件、原理、优缺点以及实际仿真结果。

PID 参数整定方法

临界比例度法 (Ziegle-Nichols算法齐格勒尼科尔斯整定方法)

是用纯比例控制器，将系统放入闭环(单位负反馈回路)中进行整定 ---> 闭环

PID控制及整定算法_pid自整定_挥剑踏苍穹的博客-CSDN博客

一文弄懂调节器的PID自整定原理和方法_正弦信号pid调节-CSDN博客

适用条件

适用于临界振幅小、振动周期长的过程控制系统

主要参考：PID控制算法与参数整定，用这几招轻松搞定!_strongerHuang的博客-CSDN博客

适用于阶跃响应曲线是个S型临界振幅不大、振荡周期较长的过程控制系统

不适用于一阶（除了一阶加纯滞后），适用于二阶以上，但不能有稳定零点(负平面零点)；

一阶不适用：要出现等幅振荡，即在高斯判稳时出现整行0，或者说有一对纯虚根；而对于一阶系统，特征根不可能成对；

对于一阶滞后系统，可以对其阶跃响应进行推导：

$Y(s)=\cfrac{1}{s}·\cfrac{e^{-ns}}{Ts+1}=\cfrac{e^{-ns}}{s}-\cfrac{e^{-ns}}{s+1/T}$ ；拉反得响应 $y(t)=u(t-n)-e^{-\cfrac{t-n}{T}}$ 但这个好像不会...

仿真发现，当闭环阶跃响应为 $Y(s)=\cfrac{1}{s}·\cfrac{e^{-ns}}{Ts+e^{-ns}}=\cfrac{1}{s}-\cfrac{T}{Ts+e^{-ns}}$ ，当 $n=\cfrac{\pi T}{2}$ 时，总会出现等幅振荡

如当T为1时， $n=\cfrac{\pi}{2}$ ，对于 $Y(s)=\cfrac{1}{s}·\cfrac{e^{-ns}}{s+e^{-ns}}=\cfrac{1}{s}-\cfrac{1}{s+e^{-ns}}$ 出现等幅振荡，拉反应该与三角函数相关（或者可能与周期性拉氏变换有关？周期信号的拉氏变换.ppt）

滞后环节的滞后时间n与一阶系统时间常数T的关系： $T=\cfrac{2n}{\pi}$ ；如果没有滞后环节，系统闭环阶跃响应应为 $y(t)=1-e^{-\cfrac{t}{T}}$

对于二阶系统阶跃响应，特征根为共轭虚根，就是阻尼比为0；关于二阶系统的阶跃响应分析：二阶系统的时域响应及动态性能(时域分析)_二阶系统响应_wanrenqi的博客-CSDN博客 关于频域Bode图分析：第十一讲频域分析法(伯德图) 时域分析： 自控原理-线性系统时域分析_pd反馈控制_M12-ll,的博客-CSDN博客

主要原理

可以参考：使用Ziegler-Nichols方法的自整定控制但不是很明白

其实主要是微分常数与P(稳定振荡周期)的正相关性：微分常数越大，快速性越好，而对于稳定振荡时过程量变化缓慢的系统(P比较大)，应该使用较为灵敏的控制，在产生变化时立即控制住；而对于P较小的灵敏系统，保守控制；

安全验证 - 知乎

PID控制器类型的选择

控制规律的选择

P: 适用于干扰变化幅度小，自衡能力强，对象滞后(τ∕T )较小，控制质量要求不高，且系统允许有一定范围余差的场合。

PI: 工艺要求静态无余差，控制对象容量滞后很小，负荷变化幅度较大，但变化过程又较缓慢的场合。

PD: 适用于控制对象T0较大的场合。对于滞后很小，信号有噪声或周期性干扰的系统不能采用微分作用。

PID: 适用于负荷变化和对象容量滞后都较大、时滞不太大且控制质量要求又较高，被控变量变化缓慢的场合。

PID控制器各个环节作用参考：PID参数整定一些总结_呆萌蜗牛的博客-CSDN博客

增大量	安定时间	滞后时间d	时间常数
Kp	稍增	增加	减少
Ki	增加	增加	稍减
Kd	减少	稍减	稍减

开环阶跃响应曲线整定 (有Z-N和C-C两套经验公式)

适用于系统传函未知，形式为开环，给予阶跃激励，记录输出，属离线方法；

上表分析Kp的整定公式是合理的

在低频段(与稳定性相关)，主要是PI控制规律起作用，提高系统型别，消除或减少稳态误差；

在中高频段(与快速性相关)主要是PD规律起作用，增大截止频率和相角裕度，提高响应速度；

基于 Z-N 法

主要参考：基于齐格勒-尼科尔斯法则(Ziegler–Nichols

基于Ziegler-Nichols法的PID参数整定_我要积分我要积分的博客-CSDN博客(给出了Z-N的改进法)

Ziegler-Nichols工程整定法

控制算法手记-自动整定方法初步

PID参数 Ziegler-Nichols基于时域响应曲线的整定反应曲线法_陈蜜蜂的博客-CSDN博客

这个原理可以猜想一下(没有查到)：

在斜率最大处做切线，与稳定值交点对应d为滞后(死区)时间，动态响应时间的测度(对象时间常数$$\tau$$)；

阶跃响应曲线的Kss与Kc反比容易理解，而如果时间常数大，即快速性差，也需要通过增大比例常数提高快速性；

积分环节中积分常数越大，积分作用越弱，即动态响应变快，但对应稳态误差较大；

难道说比例常数增大是加快上升，而积分常数增大会使动态响应提前？？确实如此

继电器法难道就是这样？给予阶跃信号分析输出的时域响应？？？？

实例：PID整定一:响应曲线法_响应曲线法整定pid参数_lijil168的博客-CSDN博客

PID参数 Ziegler-Nichols基于时域响应曲线的整定反应曲线法_陈蜜蜂的博客-CSDN博客

基于 Cohen-Coon 科恩-库恩法

与Z-N法相比，校正了缓慢稳态响应情况，即相对于开环时间常数，存在较大的死区时间（过程延迟d）的情况，因此只适用于有时间延迟的一阶模型

比例常数Kc：显而易见相当于加入了一项1/3Kss，改进后，当Kss较大时二者相同，Kss较小时，还要再大一点
积分常数：当时间常数>>d，仍为3.33d；而d>>时间常数，迫切需要通过增加微分常数来将响应提前；
微分常数：相似，当时间常数>>d，仍为0.36d；而d>>时间常数，2，通过增加微分常数来将响应提前；

二者比较

主要参考：2. 通过经典方法进行 PID 调谐_蔚蓝慕的博客-CSDN博客

简单比较：PID控制& Simulink& 标定_simulink超前校正_Jar_Lee的博客-CSDN博客

注意这里都是时域分析，时间常数体现了响应的快慢，而滞后时间，则需要考虑使用微分环节抵消系统本身滞后产生的影响，是因为系统存在滞后环节

IMC-PID 内模控制整定

计算原理主要参考：基于内模原理的PID控制器参数整定

与之类似：基于内模控制的PID参数整定及仿真.PDF

灵敏度峰值

灵敏度峰值第二章P46图片/P52 灵敏度幅值就是用于扰动抑制的整定规则

灵敏度与干扰抑制相关，灵敏度函数反映了扰动对于输出的影响；最大灵敏度Ms越小，系统抗干扰性就越好

灵敏度峰值的计算可以直接通过灵敏度公式求；而在两种整定中，设计了两种目标最大灵敏度，抗扰前提下求参

猜测：由于d放大高频噪声，所以不抗干扰；对于Ms设定值越小，也就是越抗干扰的，d作用要减弱，而快速性也变差，因此P16说产生较慢的闭环响应

但抑制噪声和抑制扰动总是存在矛盾的

是否含有积分环节

而关于含有积分环节的系统控制器仍采用积分

频域法分析系统详解及个人笔记_51CTO博客_系统的频域分析法

解释一阶系统不能靠增大K产生振荡

⭐整体比较⭐

整定方法		方法简述	本质原理	适用场景	不适用	优点	缺点
临界比例度法	Ziegle-Nichols	闭环/在线调试纯比例控制器接入到闭环控制系统中，记录等幅振荡(其实书上写的是出现持续振荡)对应的临界增益和临界周期参数，查表得出PID控制器参数；	从开环阶跃实验中辨识模型相关参数，后通过经验查询表格直接确定PID参数	一阶纯滞后系统二阶及以上系统临界振幅小、振动周期长的过程控制系统	一阶系统含稳定零点二阶某些系统时间常数较大的单容对象 (任意比例控制均稳定) 从安全性考虑不允许进行稳定边界试验的系统	简直没有发现...	调参后的响应初期常有较为明显的振荡，较为激进（可以通过减小P/I等参数来修正）；持续振荡难确定；
阶跃响应曲线	Ziegle-Nichols	开环/离线调试记录阶跃响应曲线，在曲线最大斜率(延时拐点)处做切线,求得滞后时间 t,对象时间常数 $\tau$	根据被控系统开环传递函数Nyquist曲线与负实轴交点处的增益和频率确定PID参数并将该交点移到指定位置，调整Nyquist曲线形状(环路整形方法)	有时延的一阶(一阶纯滞后) 被控对象的单位阶跃响应曲线看起来近似一条S形曲线（广义对象的响应曲线可以用“一阶+纯滞后”来近似）		破坏性小	由于简化模型只适用于特定工作频率下的特定被控对象，导致基于简化模型整定出来的控制器应用范围和性能大大受限，某些条件下甚至会导致系统失稳；
阶跃响应曲线	Cohen-Coon	开环/离线调试记录阶跃响应曲线，在曲线最大斜率(延时拐点)处做切线,求得滞后时间 t,对象时间常数 $\tau$				校正了缓慢稳态 ( $d>>\tau$ )

仿真调参【Z-N 临界振荡法】

一阶系统

一阶是不适用于临界比例度法的，因为不会产生等幅振荡，可以通过以下阶跃响应的推导证明：

经典一阶，如图P参数为P，对应于闭环系统：

$\cfrac{\cfrac{P}{s}}{\cfrac{P}{s}+1}=\cfrac{P}{s+P}$

其阶跃响应传函为

$\cfrac{1}{s}·\cfrac{P}{s+P}=\cfrac{1}{P}·(\cfrac{1}{s}-\cfrac{1}{s+P})$

拉反得响应信号为

$y(t)=\cfrac{1}{P}·(1-e^{-Pt})u(t)$

无论P怎么变化，总是会得到上图中的响应曲线；

一阶纯滞后

这个指在闭环中加入纯滞后环节，这里加入延时1，即模块 $u(t-1)$ ，对应传函 $e^{-s}$

推导一下：其阶跃响应传函为

$\cfrac{1}{s}·\cfrac{Pe^{-s}}{s+P}=\cfrac{e^{s}}{P}·(\cfrac{1}{s}-\cfrac{1}{s+Pe^{-s}})$

可以参考信号与系统P282，无失真传输：但求不出响应时域解，想过把拉变改为傅变

可以用但仍然没法求解或者 $\cfrac{1}{1-e^{-Ts}}$ 是周期的标志；

因此考虑使用Taylor展开，将纯滞后环节展开 $e^{-Ts}=\cfrac{1}{e^{Ts}}=\cfrac{1}{1+Ts+\cfrac{T^2s^2}{2!}+\cfrac{T^3s^3}{3!}+...}$ 可以用多阶环节代替：

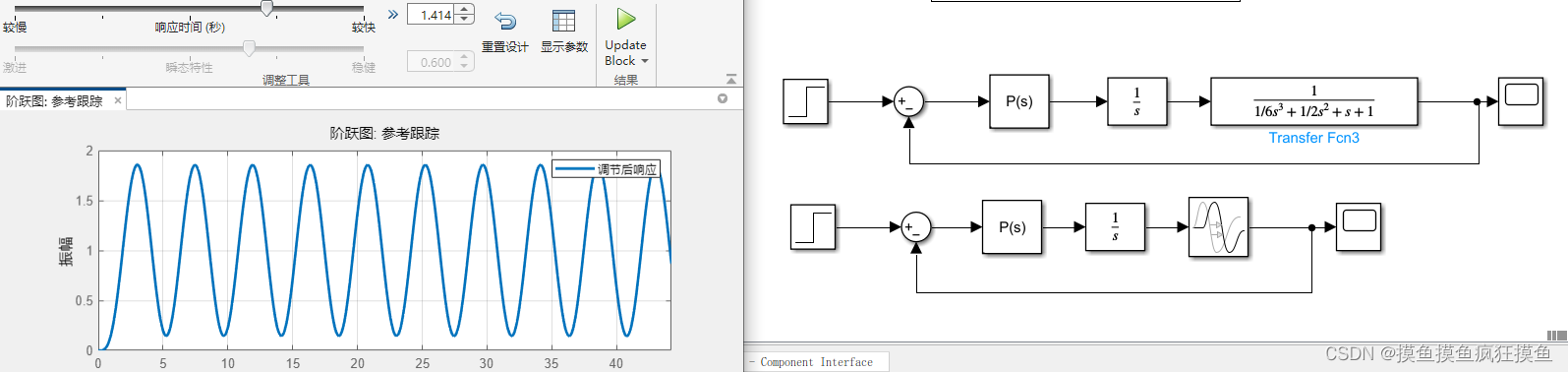
或者直接用一阶惯性环节代替：

其实T越小，用一阶惯性来近似效果越好，但上图仿真和推导发现只可能是欠阻尼的衰减振荡

二阶系统

典型二阶系统的传递函数为 $\cfrac{\omega_n^2}{s^2+2\xi\omega_ns+\omega_n^2}$ ，对其阶跃响应拉反：

$\cfrac{1}{s}\cfrac{\omega_n^2}{s^2+2\xi\omega_ns+\omega_n^2}=\cfrac{1}{s}\cfrac{\omega_n^2}{(s+\xi\omega_n+\sqrt{\xi^2-1}\omega_nj)(s+\xi\omega_n-\sqrt{\xi^2-1}\omega_nj)} =\cfrac{\omega_n^2}{2\omega_n\sqrt{1-\xi^2}j}·\cfrac{1}{s}·(\cfrac{-1}{s+\xi\omega_n+\sqrt{1-\xi^2}\omega_nj}+\cfrac{1}{s+\xi\omega_n-\sqrt{1-\xi^2}\omega_nj})=\cfrac{\omega_n}{2\sqrt{1-\xi^2}j}·[\cfrac{1}{\xi\omega_n+\sqrt{1-\xi^2}\omega_nj}(\cfrac{-1}{s}+\cfrac{1}{s+\xi\omega_n+\sqrt{1-\xi^2}\omega_nj})+\cfrac{1}{\xi\omega_n-\sqrt{1-\xi^2}\omega_nj}(\cfrac{1}{s}-\cfrac{1}{s+\xi\omega_n-\sqrt{1-\xi^2}\omega_nj})]=\cfrac{1}{2\sqrt{1-\xi^2}j}·[(\xi-\sqrt{1-\xi^2}j)(\cfrac{-1}{s}+\cfrac{1}{s+\xi\omega_n+\sqrt{1-\xi^2}\omega_nj})-(\xi+\sqrt{1-\xi^2}j)(\cfrac{1}{s}-\cfrac{1}{s+\xi\omega_n-\sqrt{1-\xi^2}\omega_nj})]=\cfrac{1}{s}+\cfrac{1}{2\sqrt{1-\xi^2}j}·[(\xi-\sqrt{1-\xi^2}j)(\cfrac{1}{s+\xi\omega_n+\sqrt{1-\xi^2}\omega_nj})+(\xi+\sqrt{1-\xi^2}j)(\cfrac{1}{s+\xi\omega_n-\sqrt{1-\xi^2}\omega_nj})]$

拉反得：

$y(t)=1+e^{-\xi\omega_n t}\cfrac{1}{2\sqrt{1-\xi^2}j}·[(\xi-\sqrt{1-\xi^2}j)e^{-\sqrt{1-\xi^2}\omega j}+(\xi+\sqrt{1-\xi^2}j)e^{\sqrt{1-\xi^2}\omega j}]=1-e^{-\xi\omega_n t}\cfrac{1}{\sqrt{1-\xi^2}}·[\xi cos(\sqrt{1-\xi^2}\omega_n t)+\sqrt{1-\xi^2}sin(\sqrt{1-\xi^2}\omega_n t)]=1-e^{-\xi\omega_n t}\cfrac{1}{\sqrt{1-\xi^2}}·[sin(\sqrt{1-\xi^2}\omega_n t+arctan\cfrac{\xi}{\sqrt{1-\xi^2}})]$

将 $\sqrt{1-\xi^2}\omega_n$ 记作 $\omega_d$ ，将 $arctan\cfrac{\xi}{\sqrt{1-\xi^2}}$ 记作 $\phi$ ，就得到了经典的二阶系统通用阶跃时域响应函数：

$y(t)=1-e^{-\xi\omega_n t}\cfrac{1}{\sqrt{1-\xi^2}}·sin(\omega_d t+\phi)$

分情况分析：

阻尼比 $\xi=0$ ：$$y(t)=1-sin(\omega_n t)$$ 等幅振荡
阻尼比 $\xi=1$ (临界阻尼)：

$y(t)=1-e^{-\xi\omega_n t}\cfrac{1}{\sqrt{1-\xi^2}}·[\xi cos(\sqrt{1-\xi^2}\omega_n t)+\sqrt{1-\xi^2}sin(\sqrt{1-\xi^2}\omega_n t)]$

$y(t)=1-e^{-\xi\omega_n t}\cfrac{1}{\sqrt{1-\xi^2}}·[sin(\sqrt{1-\xi^2}\omega_n t+arctan\cfrac{\xi}{\sqrt{1-\xi^2}})]=1-e^{-\omega_n t}[\cfrac{\sqrt{1-\xi^2}\omega_n t}{\sqrt{1-\xi^2}}+\cfrac{\cfrac{\xi}{\sqrt{1-\xi^2}}}{\sqrt{1-\xi^2}})]$

得到： $y(t)=1-e^{-\omega_n t}(\omega_n t+1)$

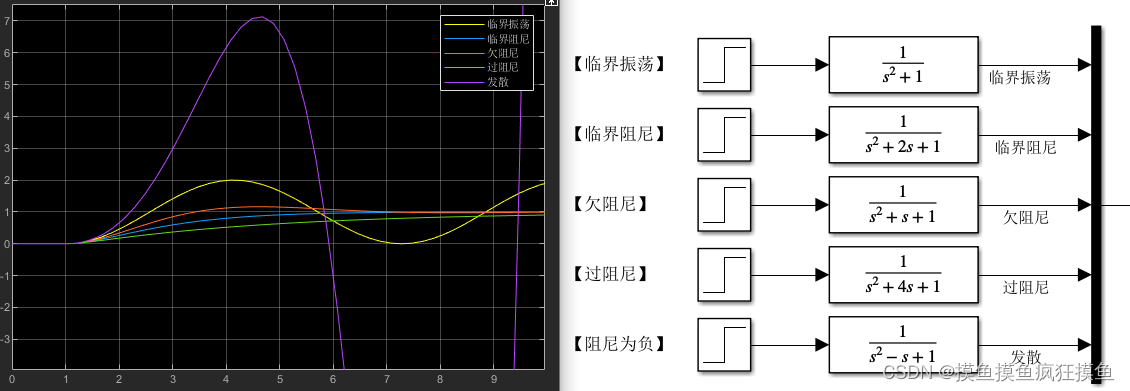
基本曲线图像：假设固有频率为1， $y(t)=-e^{-t}$

3. 欠阻尼 $\xi<1$ ： $y(t)=1-e^{-\xi\omega_n t}\cfrac{1}{\sqrt{1-\xi^2}}·sin(\omega_d t+\phi)$ 呈现一种衰减的周期振荡

4. 过阻尼 $\xi>1$ ：印象中这个很复杂又不会出题所以干脆不考虑了反正是发散

小结

可以通过系统传函的特征方程求出特征根，来判断系统阶跃响应的形式：

如对于二阶系统的特征方程 ${s^2+2\xi\omega_ns+\omega_n^2}$ ：

如果 $\xi=0$ ，得到特征根为 $\omega_nj$ ，位于虚轴上，系统临界稳定，出现等幅振荡
如果 $\xi<0$ ，得到特征根为一对位于右半平面上的共轭复根，系统发散
如果 $\xi=[0,1]$ ，得到特征根为一对位于左半平面上的共轭复根，系统稳定
如果 $\xi=1$ ，得到特征根为 $-\omega_n$ ，位于负半平面，系统稳定
如果 $\xi>1$ ，特征根必然是一对位于实轴上的实根，一负一正，系统稳定？

调参

因此在闭环的二阶控制系统中，设开环系统的传函为： $\cfrac{1}{s^2+as}$ ，加入PID控制器的P比例控制：

得到闭环传函为 $\cfrac{P}{s^2+as+P}$ ，映射为经典二阶传函形式： $\omega_n=\sqrt{P},\xi=\cfrac{a}{2\sqrt{P}}$

高阶系统

K=7.5，P=3.36s

P控制器应选用：计算出为：3.75

PI控制器选用： $I=\cfrac{1}{\tau_i}=\cfrac{1.2}{P_o}$ ，计算出分别为：3.375 和 0.3571

PID控制器选用： $I=\cfrac{1}{\tau_i}=\cfrac{2}{P_o}$ ； $D=\cfrac{P_o}{8}=\cfrac{1}{4I}$ ，计算出分别为：4.5、0.56、0.42

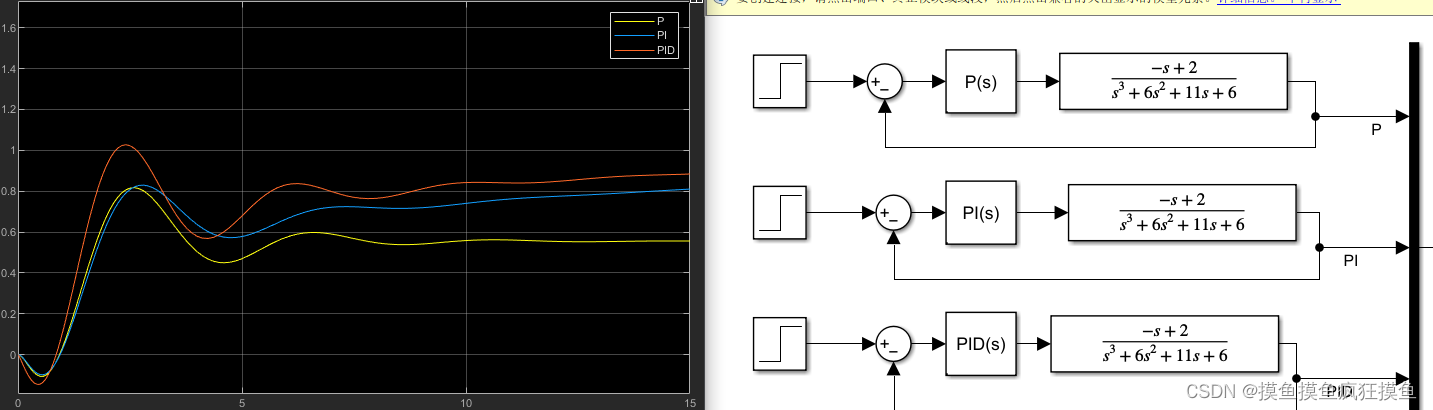
我竟觉得跟上面尝试的结果差不多...都是振荡如此严重...而且在纯用P时会出现比较大的稳态误差；

如果要修正这种不良结果，可以考虑减小K，减小I，即可以选用

； $I=\cfrac{1}{\tau_i}=\cfrac{1}{2.2P_o}$ ，计算出分别为：2.3475 和 0.1353

这结果好多了...

而且发现如果时间常数较大，在整定时无论怎么调节K总会产生持续的振荡

而如果有稳定的零点，将会导致无论如何调P，系统总是稳定、没有振荡的，连一点超调都没有

P越大，超调越小（内环控制允许超调？？？？）

仿真调参【阶跃响应曲线法】

典型一阶延迟模型：

选取 $\cfrac{2}{2s+1}·e^{-2s}$ 开环阶跃响应： $\cfrac{K_{ss}}{\tau_M s+1}·e^{-ds}$

通过响应中 $Ys=2;Y_0=0;U_s=1;U_0=0;d=2;\tau_M=2$ 斜率可以通过对原图像求导得到是1，画图可得2

能和设计的系统得到验证，以此确定PID参数：

Z-N 阶跃响应调参查表

$P:K_c=\cfrac{\tau_M}{K_{ss}d}$

$PI:K_c=0.9\cfrac{\tau_M}{K_{ss}d}$ ； $\tau_I=3d$

$PID:K_c=1.2\cfrac{\tau_M}{K_{ss}d};\tau_I=2d;D=0.5d$

(注意在simulink中的参数I是这里的倒数，并乘以参数Kc，或者选择用理想型的代替并行的)

C-C 阶跃响应调参查表

$P: K_c=\cfrac{\tau_M}{K_{ss}d}(1+\cfrac{d}{3\tau_M})$

$PI:K_c=\cfrac{\tau_M}{K_{ss}d}(0.9+\cfrac{d}{12\tau_M});\tau_I=\cfrac{d(30\tau_M+3d)}{9\tau_M+20d}$

$PID:K_c=\cfrac{\tau_M}{K_{ss}d}(\cfrac{4}{3}+\cfrac{d}{4\tau_M});\tau_I=\cfrac{d(32\tau_M+6d)}{13\tau_M+8d};D=\cfrac{4d\tau_M}{11\tau_M+2d}$

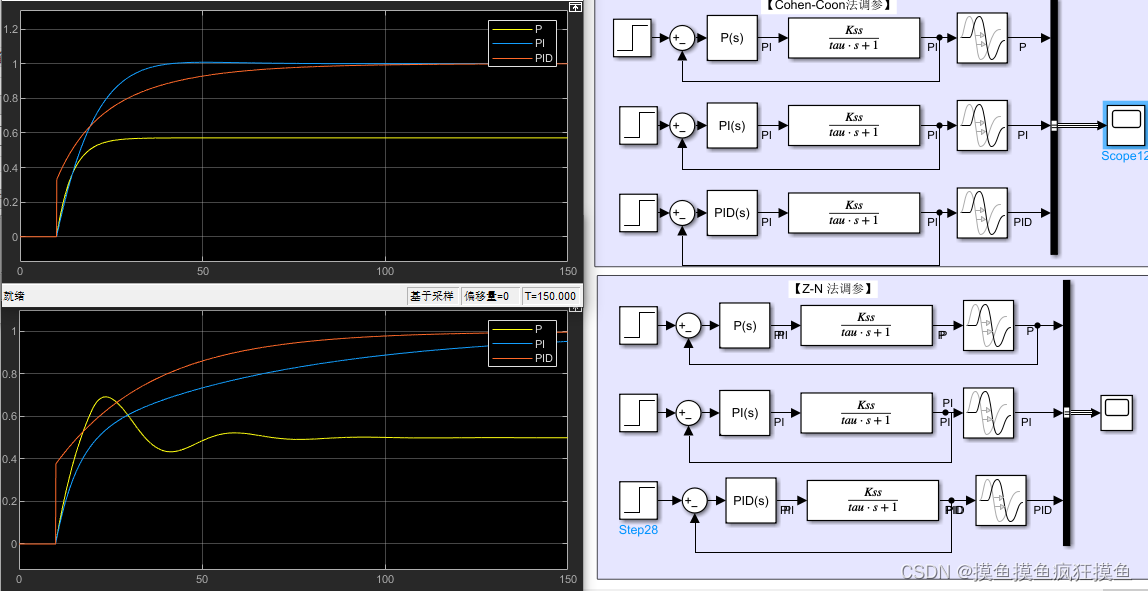
仿真（CC/ZN对比）

选取较小的时间常数与滞后时间

显然此时：

整体上，C-C法在稳定性和快速性方面都更好；

但纯比例控制下，两种方法都有稳态误差(这点其实很难，有没有延时模块都会存在误差)

可以用公式推导一下：

不考虑滞后，纯比例控制下的阶跃响应传函为 $\cfrac{PK_{ss}}{PK_{ss}+1}(\cfrac{1}{s}-\cfrac{PK_{ss}}{\tau_Ms+PK_{ss}+1})$ ，最终误差项 $\cfrac{1}{PK_{ss}+1}$

只有使劲增大比例系数P才能使误差减小，尝试将这里的从0.5调整到10和100：

但一旦加上延时模块，使用大比例系数很可能导致系统的发散

当选用大时间常数（tau/d比较大）

显然此时：

如果纯比例控制： Cohen-Coon调参无超调，但两种方法都存在稳态误差(但时间常数大、P大，误差较小)；

如果使用PID控制：两种方法的PI/PID控制效果相似，两种方法都不会有误差；

因此如果时间常数与d时滞的比值 $\cfrac{\tau_M}{d}$ 很大时，用纯比例控制才不会有很大的误差，而用C-C法能避免超调

尝试用了下比值为100的：

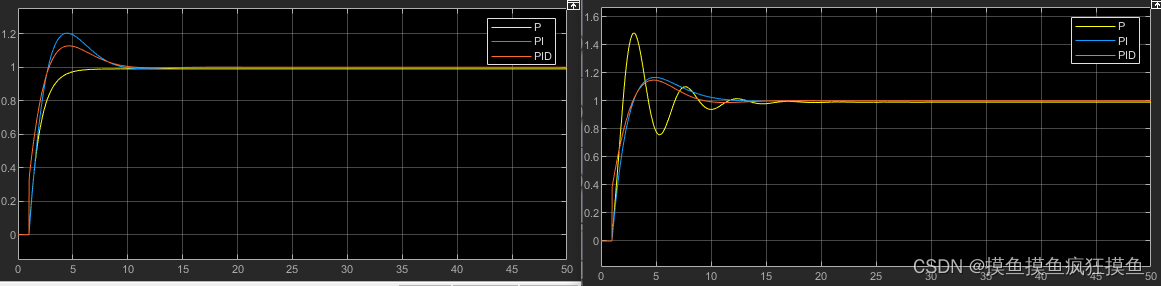
当选用大延时时间（tau/d比较小）

，根据上面的分析，纯比例肯定会误差很大，但很离谱的是ZN法直接发散了

C-C控制很慢，但毕竟控制住了

如果比值 $\cfrac{\tau_M}{d}$ 过小时，用Z-N法调参甚至会使系统发散（而 $\cfrac{\tau_M}{d}$ 较小会导致纯比例控制误差更大、CC控制变慢）

当选用较大的时间常数与滞后时间

τM=10，Kss=2，d=10 并没有发散，不过Z-N的控制速度更慢了

此时如果把Kss也增加到10，两种方法的仿真图像基本未变：

参数Kss的变化对几种控制都不会有影响

⭐仿真结论分析⭐

重点关注图像中的 $\cfrac{\tau_M}{d}$ 比值(简记为时滞比)，无需关注：

除非时滞比很大时可用，否则使用纯比例控制都会有大稳态误差，且Z-N法的纯比例总有超调(初始振荡)
当时滞比较大时，两种调参方法控制效果相似
当时滞比较小时，用Z-N法调参甚至会使系统发散，纯比例控制误差非常大；C-C的PI/PID可以控制 (但较慢)
当时滞比约为1时，使用两种方法的PI/PID均可，但C-C法控制快 (且PI更快) d或tau较大时可选C-C

简而言之，任何时候用 C-C 的 PI 或者 PID 都没错

⭐阶跃响应法参数计算代码⭐

参数算起来有点麻烦，要不写成代码吧：


%%---------------------开环阶跃响应图像的参数--------------------------
d = ;tau = ;Kss = ;%%d是滞后时间、tau为时间常数
%%---------------------注意simulink中控制器要选用理想型(不用并行)
%%---------------------Z-N法-----------------------------------------------------
K1_zn=tau/Kss/d;
K2_zn=tau/Kss/d*0.9;I2_zn=1/3/d;
K3_zn=tau/Kss/d*1.2;I3_zn=1/2/d;D3_zn=0.5*d;
%%---------------------Cohen-Coon法-----------------------------------------------
K1_cc=tau/Kss/d*(1+d/3/tau);
K2_cc=tau/Kss/d*(0.9+d/12/tau);I2_cc=1/(d*(20*tau+3*d)/(9*tau+20*d));
K3_cc=tau/Kss/d*(4/3+d/4/tau);I3_cc=1/(d*(32*tau+6*d)/(13*tau+8*d));D3_cc=4*d*tau/(11*tau+2*d);

二阶延时系统的模拟

尝试用 $\cfrac{e^{-s}}{s+1}$ 来模拟 $\cfrac{e^{-s}}{s^2+s+1}$ ，二者的阶跃响应如图：

左图是Z-N法，右图是C-C

系统的开环阶跃和闭环PID如图所示：

发现是不是用不带延时模块的二阶系统，和一阶延时更近似呢？

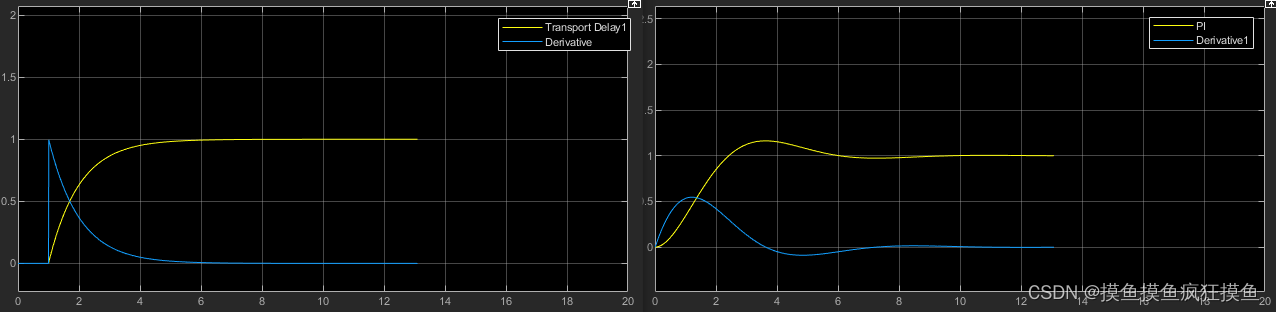
不过看起来控制效果没啥变化

将最终到达稳态值的时间点6作为稳定点，重新设置时间常数为1，时滞为s=0.5，可以得到：

虽然这两个的阶跃响应图像已经很接近了，但不知道为什么就是振荡的很厉害，但整体来说 PID 勉勉强强；

提出修改措施：

更精准的函数模拟（控制效果反推）
讨论控制效果与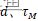的关系

函数模拟

对于高阶系统的阶跃响应图像，总是呈现 S 形，选取图像上斜率最大的一点作切线，与起始位置和终止平衡位置的交点分别对应d和 $\tau_M$ ：

垃圾桶（果然最开始做的总是垃圾）

拉线得到（之后发现这个有误），将参数输入到一阶延时的模拟：

感觉不是贴合的很紧密

优化函数模拟

同样的，Z-N法的控制效果优于C-C，并且两种方法均是PID控制效果更好；

如果把时间常数减小：τM=70 感觉吻合的很不错

而Z-N(右图)仍然优于C-C：

而且与调整参数前相比，振荡有所减弱

所以真正可靠的参数选择应该以斜率最大值点为分界点，其左为时滞d，其右为时间常数τM

对于这个系统的响应曲线来说，分界点坐标为(80.215，0.1626)，

作切线与两平行线交点分别为（36，0）（155，0.5），因此

阶跃响应对比：

而在控制时都没有给高阶系统加入延时模块，如果加入延时进行控制，如延时100s：
：这时选取PID的控制效果更好

⭐总结⭐

在用一阶延时模拟高阶延迟系统时，通过高阶的阶跃响应S曲线，求导取最大值点，做切线交于起始位置和平衡位置，零点到前点、切点与后点的时间间隔分别为d、τM，再根据前文总结表格选择最优的控制方法

在上面的控制中，高阶系统并未加入延时模块。因此d的大小其实与系统无关，而是决定了参数，选用不同的d：

由于上面的实例均为时滞比较大的情况，修改高阶函数的滞后时间为100s，取，阶跃响应：

C-C法中的PI控制最优，符合之前表格中的结论

而如果将d改为75，即与时间常数相同，得到仿真参数如下：

参数修正

加入延时模块

在这里给实际受控系统加入延时模块：

对于使用上面的方法得到时滞两个参数，是否可以找到方法去优化这两个参数？

尝试使用PID自动tune，调出来的参数与此前C-C法的PID参数对比：

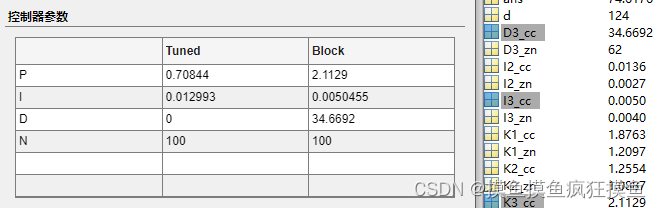
由于根本没使用到微分项，因此改为和PI控制器进行比较：

修正后的控制效果果然更好

如果一开始，就以斜率极大值切点横坐标作为时滞参数d，即d=160.5，代入

控制效果更好一点

⭐总结⭐

如果受控高阶系统中不含延时模块，如 $\cfrac{0.5}{(30s+1)^3 }$ ，在阶跃响应图中找到切点到右点的间隔时间常数后，给其一个和时间常数接近或稍大的时滞，代入公式求参；

如果高阶系统本身就含有延时模块，如 $\cfrac{0.5e^{-20s}}{(30s+1)^3}$ ，可以在响应图像的基础上稍微修改一下对于参数的确定，以切点的横坐标作为时滞d往往更加合适；

例如在按照常规思路算出左点横坐标d=36，代入后：

而如果选取切点作为d=80：

控制效果改善了一些

当然如果去看同样的参数控制的无延迟模块的效果，由于此时符合d与相近的原则，控制效果还可以

仿真调参【IMC-PID 内模控制整定】

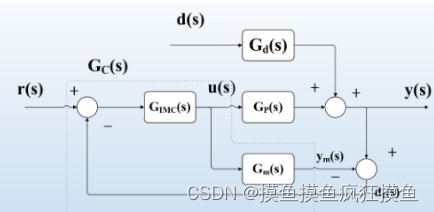
内模控制框图与传函推导：是过程

$Y(s)=\cfrac{G_pG_{IMC}}{1+G_{IMC}(G_p-G_m)}r(s)+\cfrac{1-G_{IMC}G_m}{1+G_{IMC}(G_p-G_m)}d(s)$

而内模控制PID整定的原理就是输入传函计算中，虚线框内的 $G_c(s)=\cfrac{G_{IMC}}{1-G_{IMC}G_m}$ ，就相当于所选用的PID控制

而内模控制消除干扰d的最大原则是过程函数，即与被控系统的形式相同，基于内模原理的PID

其参数计算公式正是据此推导，同样参考：基于内模原理的PID控制器参数整定

对于被控系统 $G_p=G_m=\cfrac{K_{ss}(1-as)e^{-ds}}{(\tau_Ms+1)^r}={G_{m+}}G_{m-}$ ， $G_{m-}=\cfrac{1}{(\tau_Ms+1)^r}$ ，

根据内模控制原理 $G_{IMC}=\cfrac{1}{G_{m-}(\epsilon s+1)^r}$ (含低通滤波)，得到 $\cfrac{Y(s)}{r(s)}=\cfrac{K_{ss}(1-as)e^{-ds}}{(\epsilon s+1)^r}$

代入可得： $G_c=\cfrac{1}{G_{m-}[(\epsilon s+1)^r-G_{m+}]}=\cfrac{1}{s}f(s)$

将其taylor展开： $G_c=\cfrac{1}{s}(f(0)+f'(0)s+\cfrac{f''(0)}{2!}s^2)=\cfrac{1}{s}[f'(0)(\cfrac{f(0)}{f'(0)}+s+\cfrac{f''(0)}{2f'(0)}s^2)]$ $=\cfrac{1}{s}K_c(\cfrac{1}{I}+s+Ds)$

就可以得到 $Kc=f'(0);I=\cfrac{f'(0)}{f(0)};D=\cfrac{f''(0)}{2f'(0)}$

⭐结论⭐

$I=\tau_M+\cfrac{\tau_M^2}{2(\epsilon+\tau_M)},K_c=\cfrac{2\epsilon\tau_M+3\tau_M^2}{2K_{ss}(\epsilon+\tau_M)^2},D=\cfrac{4\epsilon\tau_M^2+7\tau_M^3}{6(\epsilon+\tau_M)(2\epsilon+3\tau_M)}$ (参考链接)

而书上P15有各种系统的结论：ϵ是所设计的理想的一阶延时系统(相当于低通滤波)

关于一阶延迟 $G_m(s)=\cfrac{K_{ss}e^{-ds}}{\tau_Ms+1}$ ： $Kc=f'(0)=\cfrac{\tau_M}{K_{ss}(\epsilon+d)}$ ， $I=\cfrac{f'(0)}{f(0)}=\tau_M$ （和推导吻合）

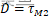
关于二阶延迟 $G_m(s)=\cfrac{K_{ss}e^{-ds}}{(\tau_{M1}s+1)(\tau_{M2}s+1)}$ ： $Kc=f'(0)=\cfrac{\tau_{M1}}{K_{ss}(\epsilon+d)}$ ，，

而修正之后 $I=min(\tau_{M1},4(\epsilon+d))$

关于 $G_m(s)=\cfrac{K_{ss}e^{-ds}}{s}$ ： $Kc=f'(0)=\cfrac{1}{K_{ss}(\epsilon+1)}$ ，

关于 $G_m(s)=\cfrac{K_{ss}e^{-ds}}{s(\tau_Ms+1)}$ ： $Kc=f'(0)=\cfrac{1}{K_{ss}(\epsilon+1)}$ ，，

关于 $G_m(s)=\cfrac{K_{ss}e^{-ds}}{s^2(\tau_Ms+1)}$ ： $Kc=f'(0)=\cfrac{1}{K_{ss}(\epsilon+1)}$ ，，

仿真

一阶延迟

对于一阶延迟系统 $G_m(s)=\cfrac{0.5e^{-20s}}{30s+1}$ ，仿真并与C-C法相比较：

可以看出IMC方法确实更加优秀

二阶延迟

对于二阶延迟系统 $G_m(s)=\cfrac{0.5e^{-20s}}{(30s+1)(40s+1)}$ ，先通过阶跃响应得到其一阶延迟近似(d=54.5，tau=70)

仿真并与C-C法对比，可以发现IMC更优

而如果实际系统中的延时模块去除后，仿真可得：（左为二阶，右为一阶）

带有延时模块：
d=20；tau1=30，tau2=40（C-C法的等效是d=40,tau=70）

d=20，tau1=5，tau2=1（C-C法等效 d=22，tau=6，为小时滞比）

d=5，tau1=30，tau2=40（C-C法等效 d=40，tau=70，为大时滞比）

⭐总结⭐

综合方法的简便性、可靠性等因素：

当被控系统不含有时滞模块时，使用Z-N/C-C或IMC方法均可，对于二阶系统使用IMC更为简便；

当被控系统中含有时滞模块时，使用IMC可以减弱振荡的幅度；

对于二阶延时系统，当被控系统的时间常数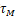较大时，使用IMC一般快速性优于C-C法，但C-C的PID超调小；

IMC的计算代码：

%%---------------------开环阶跃响应图像参数
d = ;tau = ;Kss = ;epsi = ;tau1 = ;tau2 = ;
%%---------------------注意simulink中控制器要选用理想型(不用并行)
%%---------------------IMC-PID法_适用于一阶延迟系统
K1_imc=tau/Kss/(epsi+d);I1_imc=1/tau;
%%------与C-C法相比较
K1_cc=tau/Kss/d*(1+d/3/tau);
K2_cc=tau/Kss/d*(0.9+d/12/tau);I2_cc=1/(d*(20*tau+3*d)/(9*tau+20*d));
K3_cc=tau/Kss/d*(4/3+d/4/tau);I3_cc=1/(d*(32*tau+6*d)/(13*tau+8*d));D3_cc=4*d*tau/(11*tau+2*d);
%%---------------------IMC-PID法_适用于二阶延迟系统
K2_imc=tau1/Kss/(epsi+d);I2_imc=1/min(tau1,4*(epsi+d));D2_imc=tau2;
%%---------------------IMC-PID法_适用于积分延迟系统
K3_imc=1/Kss/(epsi+d);I3_imc=1/4/(epsi+d);

仿真调参【P-V法】

只适用于一阶延时系统，对于 $G_m(s)=\cfrac{0.5e^{-20s}}{30s+1}$ ，灵敏度峰值分别为1.4和2的仿真结果如下：

如果修改一下参数，对于 $G_m(s)=\cfrac{0.5e^{-20s}}{5s+1}$ ，灵敏度峰值分别为1.4和2的仿真结果如下：

两种情况好像都是PI控制效果更好，与之前的IMC或者C-C法相比较：

仿真

大时滞比

对于d=5，tau=20的大时滞比：PV法控制结果：

C-C法与Z-N法：

小时滞比

对于d=20，tau=5的小时滞比：PV法控制结果：

C-C法与Z-N法：

去掉延时模块：

⭐总结⭐

P-V法只适用于一阶延时系统，对于时滞参数d大的系统，控制效果优于IMC或C-C法；
如果被控系统不含有延时模块，则C-C法或Z-N法都能取得比P-V超调更小的控制效果；
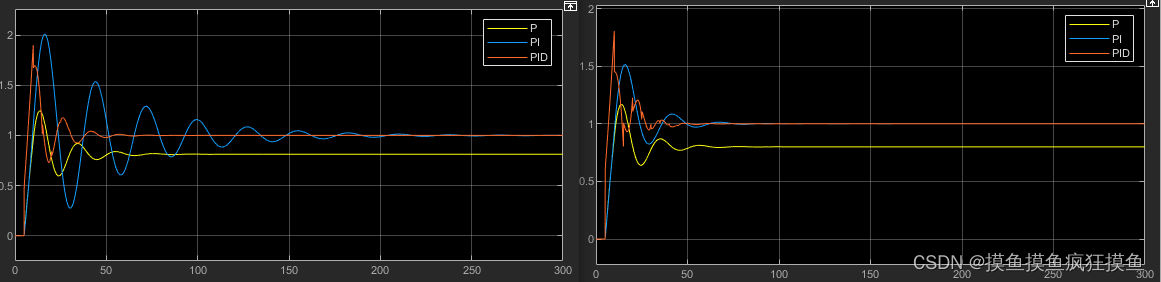
对于P-V法本身而言，灵敏度峰值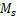较大时，控制较快，但容易有振荡，无论什么时候选择灵敏度峰值较小的参数调整更好；PI控制器超调小，PID超调较大；

参数计算代码：

%%---------------------开环阶跃响应图像参数
d = ;tau = ;Kss = ;
%%---------------------注意simulink中控制器要选用理想型(不用并行)
%%---------------------P-V   PI控制  灵敏度峰值分别为1.4/2
K1_pv=(0.2958*(d/(d+tau))^(-1.014)-0.2021)/Kss;I1_pv=1/tau/(1.624*(d/tau)^0.2269-0.5556);
K2_pv=(0.5327*(d/(d+tau))^(-1.029)-0.2428)/Kss;I2_pv=1/tau/(1.44*(d/tau)^0.4825-0.1019);
%%---------------------P-V   PID控制  灵敏度峰值分别为1.4/2
K3_pv=(0.1724*(d/(d+tau))^(-1.259)-0.05052)/Kss;I3_pv=1/tau/(0.5968*(d/tau)^0.6388+0.07886);
D3_pv=tau*(0.5856*(d/tau)^0.5004-0.1109);
K4_pv=(0.2002*(d/(d+tau))^(-1.414)+0.06139)/Kss;I4_pv=1/tau/(0.446*(d/tau)^0.9541+0.1804);
D4_pv=tau*(0.6777*(d/tau)^0.4968-0.1499);