五大经典智能算法实现机器人路径规划，包含简单路径与复杂路径，详细对比实验...

本期文章采用五大经典的智能优化算法，对机器人路径进行规划。

五大经典算法分别是：粒子群算法(PSO)，遗传算法(GA)，差分进化算法(DE)，灰狼优化算法(GWO)，麻雀优化算法(SSA)。

学会这五种算法后，其他任何智能优化算法可以随意替换！地图也是可以随意更改！

参考一些论文，还可以将改进的智能算法用于机器人路径规划中，突出改进智能算法的优势！

接下来先上结果图：其中，红线表示遗传算法，黄线表示麻雀算法，蓝线表示粒子群算法，绿线表示差分进化算法，青线表示灰狼算法。

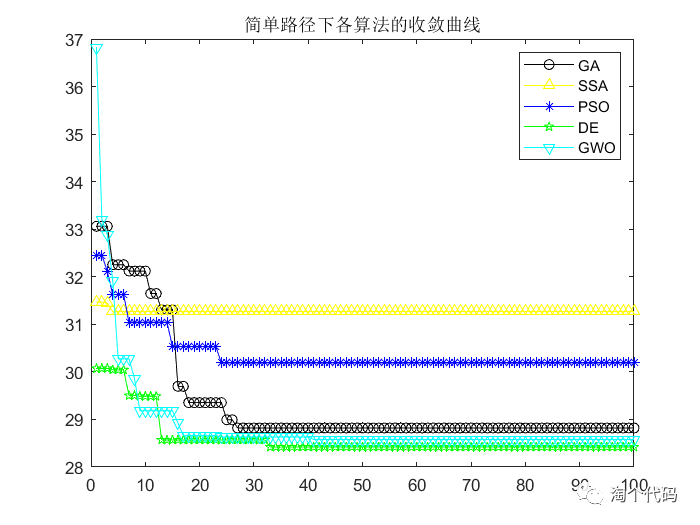
简单路径规划结果

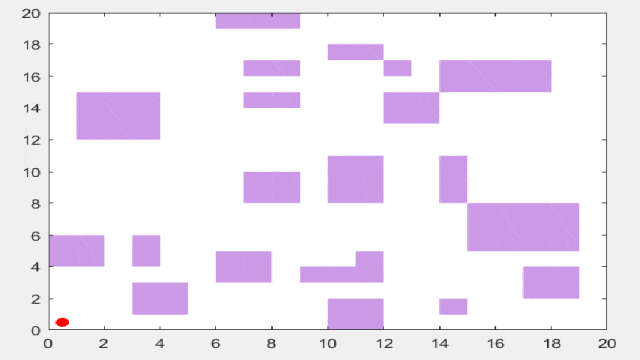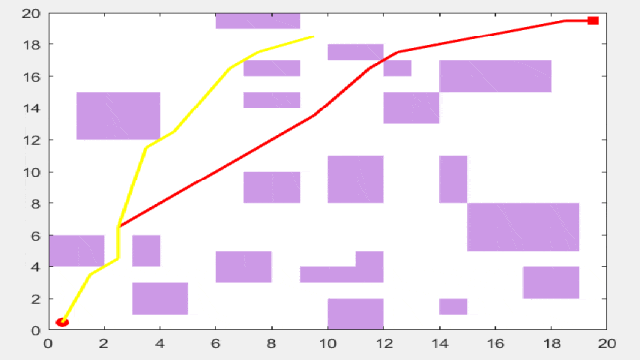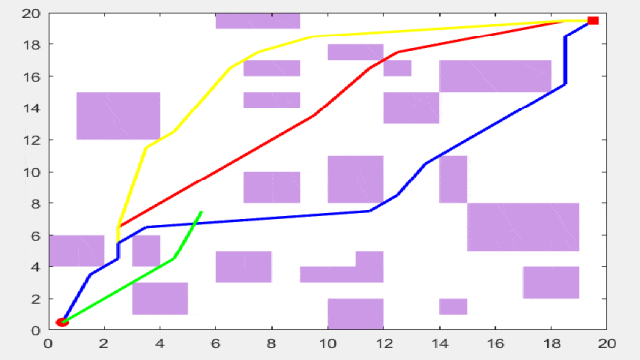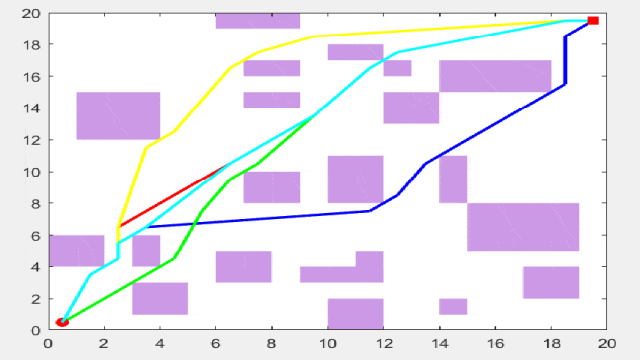
复杂路径规划结果

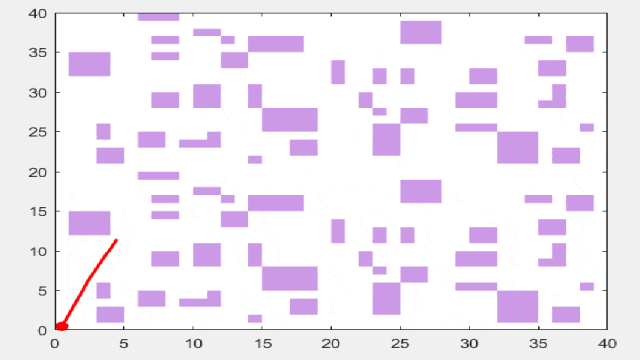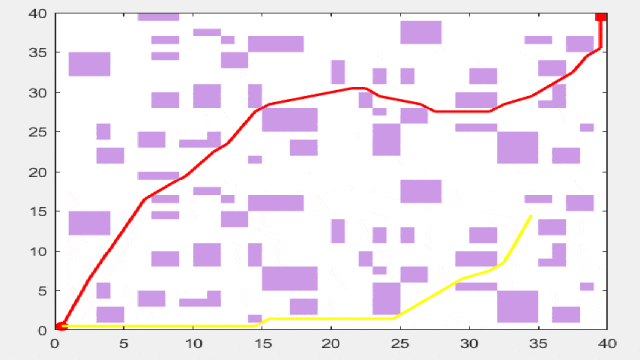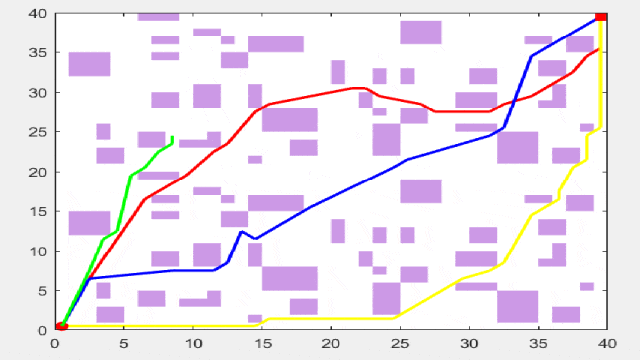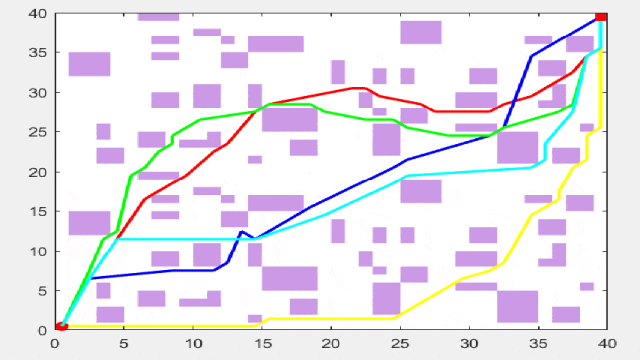
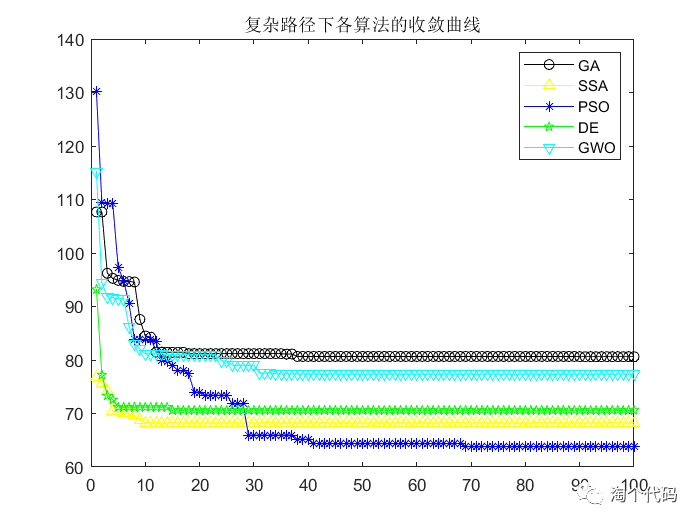
在复杂路径下，其实更能展现一个算法的优劣！因此可以将改进的智能算法用于此模型中，算法替换十分简单！

部分代码展示

clc
clear
close all
tic
%% 地图
G=[0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0; 
   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0; 
   0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0; 
   0 0 0 0 0 0 0 1 1 0 0 0 1 0 1 1 1 1 0 0; 
   0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0; 
   0 1 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 0 0 0; 
   0 1 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0;
   0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0; 
   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0; 
   0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0; 
   0 0 0 0 0 0 0 1 1 0 1 1 0 0 1 0 0 0 0 0; 
   0 0 0 0 0 0 0 1 1 0 1 1 0 0 1 0 0 0 0 0; 
   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0; 
   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0; 
   1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0; 
   1 1 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0; 
   0 0 0 0 0 0 1 1 0 1 1 1 0 0 0 0 0 1 1 0; 
   0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0; 
   0 0 0 1 1 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0; 
   0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0;];


num = size(G,1);
for i=1:num/2  
    for j=1:num
        m=G(i,j);
        n=G(num+1-i,j);
        G(i,j)=n;
        G(num+1-i,j)=m;
    end
end
%% 
S = [1 1];   
E = [num num];  
G0 = G;
G = G0(S(1):E(1),S(2):E(2)); 
[Xmax,dimensions] = size(G); X_min = 1;         
dimensions = dimensions - 2;            


%% 参数设置
max_gen = 100;    % 最大迭代次数
num_polution = 50;         % 种群数量


fobj=@(x)fitness(x,G);
[Best_score,Best_pos,GA_curve]=GA(num_polution,max_gen,X_min,Xmax,dimensions,fobj,G);
%结果分析
Best_pos = round(Best_pos);
disp(['GA算法寻优得到的最短路径是：',num2str(Best_score)])
route = [S(1) Best_pos E(1)];
path_GA=generateContinuousRoute(route,G);
path_GA=GenerateSmoothPath(path_GA,G);  
path_GA=GenerateSmoothPath(path_GA,G);


[Best_score,Best_pos,SSA_curve]=SSA(num_polution,max_gen,X_min,Xmax,dimensions,fobj,G);
%结果分析
Best_pos = round(Best_pos);
disp(['SSA算法寻优得到的最短路径是：',num2str(Best_score)])
route = [S(1) Best_pos E(1)];
path_SSA=generateContinuousRoute(route,G);
path_SSA=GenerateSmoothPath(path_SSA,G);  
path_SSA=GenerateSmoothPath(path_SSA,G);


[Best_score,Best_pos,PSO_curve]=PSO(num_polution,max_gen,X_min,Xmax,dimensions,fobj,G);
%结果分析
Best_pos = round(Best_pos);
disp(['PSO算法寻优得到的最短路径是：',num2str(Best_score)])
route = [S(1) Best_pos E(1)];
path_PSO=generateContinuousRoute(route,G);
path_PSO=GenerateSmoothPath(path_PSO,G);  
path_PSO=GenerateSmoothPath(path_PSO,G);


[Best_score,Best_pos,DE_curve]=DE(num_polution,max_gen,X_min,Xmax,dimensions,fobj,G);
%结果分析
Best_pos = round(Best_pos);
disp(['DE算法寻优得到的最短路径是：',num2str(Best_score)])
route = [S(1) Best_pos E(1)];
path_DE=generateContinuousRoute(route,G);
path_DE=GenerateSmoothPath(path_DE,G);  
path_DE=GenerateSmoothPath(path_DE,G);


[Best_score,Best_pos,GWO_curve]=GWO(num_polution,max_gen,X_min,Xmax,dimensions,fobj,G);
%结果分析
Best_pos = round(Best_pos);
disp(['GWO算法寻优得到的最短路径是：',num2str(Best_score)])
route = [S(1) Best_pos E(1)];
path_GWO=generateContinuousRoute(route,G);
path_GWO=GenerateSmoothPath(path_GWO,G);  
path_GWO=GenerateSmoothPath(path_GWO,G);




%% 画寻优曲线
figure(1)
plot(GA_curve,'k-o')
hold on
plot(SSA_curve,'y-^')
hold on
plot(PSO_curve,'b-*')
hold on
plot(DE_curve,'g-P')
hold on
plot(GWO_curve,'c-v')
legend('GA','SSA','PSO','DE','GWO')
title('简单路径下各算法的收敛曲线')

代码目录

其中simplemain.m是简单路径规划，complexmain.m是复杂路径规划。运行这两个脚本文件即可！

点击下方卡片获取更多代码！