前言
点云处理中常用到平面模型和圆柱模型分割点云或者精确确定目标点云范围。平面方程可以根据邻域点集使用最小二乘法估计得出,但是圆柱方程使用最小二乘法却没有线性方程参数估计那么简单。使用最小二乘法估计模型参数的抗粗差(噪声数据)能力不强,这也促进了稳健估计方法的研究。当前以有大量的稳健估计方法可供选择使用,如:RANSAC、BaySAC、Hough变换、Random Hough变换、极大似然法、最小中值法等等,本文中将对最简单的RANSAC稳健估计方法进行讲解。RANSAC算法笔者用的较多,具有迭代次数少,抗粗差能力强的特点。算法具体过程很多点云处理方面的论文中都有涉及,再此就不赘述了(等毕业答辩后会花时间整理算法流程,并把C++代码共享)。这篇博客里就基于PCL利用RANSAC算法对平面参数和圆柱参数进行求解。
平面方程参数估计
常用的平面方程是平面的法线式:ax+by+cz=d,其中a^2+b^2+c^2=1,d>0,(a,b,c)为平面法矢,d为原点至平面的距离,这四个参数可以确定一个平面。
//存放局内点索引
pcl::PointIndices::Ptr inliers (new pcl::PointIndices);
//创建分割对象
pcl::SACSegmentation<pcl::PointXYZ> seg;
//选择模型系数是否需要优化
seg.setOptimizeCoefficients (true);
//设置模型类型
seg.setModelType (pcl::SACMODEL_PLANE);
//设置模型估计方法
seg.setMethodType (pcl::SAC_RANSAC);
//设置最大迭代次数
seg.setMaxIterations(10000);
//距离阈值(离散点到模型表面距离)
seg.setDistanceThreshold (0.01);
//输入点云
seg.setInputCloud (cloud);
//计算模型参数和得到符合此模型的局内点索引
seg.segment (*inliers, *coefficients);
//输出平面模型的四个参数
std::cerr << "Model coefficients: " << coefficients->values[0] << " "
<< coefficients->values[1] << " "
<< coefficients->values[2] << " "
<< coefficients->values[3] << std::endl;
平面模型参数估计结束。
圆柱方程参数估计
圆柱方程可以表示为:(x-x0)^2+(y-y0)^2+(z-z0)^2-r^2=[l(x-x0)+m(y-y0)+n(z-z0)]^2/(l^2+m^2+n^2)。下图为空间圆柱示意图。
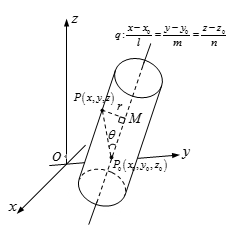
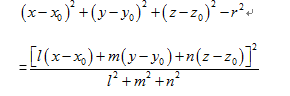
其中,(x0,y0,z0)为圆柱轴线L上一点,(l,m,n)为圆柱轴线L方向向量,r为圆柱的半径,这七个参数可以确定一个圆柱方程。
下面代码的含义和估计平面参数时代码含义基本一致,不介绍了。
// Create the segmentation object for cylinder segmentation and set all the parameters
seg.setOptimizeCoefficients(true);
seg.setModelType(pcl::SACMODEL_CYLINDER);
seg.setMethodType(pcl::SAC_RANSAC);
seg.setNormalDistanceWeight(0.1);
seg.setMaxIterations(10000);
seg.setDistanceThreshold(0.1);
seg.setRadiusLimits(0, 0.5);
seg.setInputCloud(cloud);
seg.setInputNormals(cloud_normals);
// Obtain the cylinder inliers and coefficients
seg.segment(*inliers_cylinder, *coefficients_cylinder);
std::cerr << "Cylinder coefficients: " << *coefficients_cylinder << std::endl;
// Write the cylinder inliers to disk
extract.setInputCloud(cloud);
extract.setIndices(inliers_cylinder);
extract.setNegative(false);
pcl::PointCloud<PointT>::Ptr cloud_cylinder(new pcl::PointCloud<PointT>());
extract.filter(*cloud_cylinder);
if (cloud_cylinder->points.empty())
std::cerr << "Can't find the cylindrical component." << std::endl;
else
{
std::cerr << "PointCloud representing the cylindrical component: " << cloud_cylinder->points.size() << " data points." << std::endl;
writer.write("table_scene_mug_stereo_textured_cylinder.pcd", *cloud_cylinder, false);
}计算效果

平面和圆柱(杯子)参数

平面和圆柱(杯子)分割结果










 本文介绍如何使用RANSAC算法进行点云处理中的平面和圆柱模型参数估计。通过设置不同的参数,实现从点云数据中精确提取平面和圆柱特征。
本文介绍如何使用RANSAC算法进行点云处理中的平面和圆柱模型参数估计。通过设置不同的参数,实现从点云数据中精确提取平面和圆柱特征。
















 1674
1674

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








