1. 适用于RxRyRz顺序的旋转矩阵与欧拉角变换关系
1.1. 基本旋转矩阵

1.2. 欧拉角->旋转矩阵

相乘后,得:
注意这个结果与以相反顺序绕固定轴旋转三次得到的结果完全相同!总之,这是一个不太直观 的结果:三次绕固定轴旋转的最终姿态和以相反顺序三次绕运动坐标轴旋转的最终姿态相同。因为式(2-71)和式(2-64)等价,所以无需通过旋转矩阵的反复计算去求Z-Y-X欧拉角。也就是说,式(2-66)也可用来求解同一个已知旋转矩阵的Z-Y-X欧拉角。
1.3. 旋转矩阵->欧拉角


Eigen自带的转换函数会出现欧拉角跳变的现象,虽然结果上没有问题,但使用起来不直观,这里提供一个自定义的转换方式,输出的欧拉角顺序是yaw, pitch, roll
Eigen::Vector3d ToYPRAngles(const Eigen::Matrix3d &rotation) {
Eigen::Vector3d ypr;
if (rotation(2, 0) < 1) {
if (rotation(2, 0) > -1) {
ypr.y() = std::asin(-rotation(2, 0));
ypr.x() = std::atan2(rotation(1, 0), rotation(0, 0));
ypr.z() = std::atan2(rotation(2, 1), rotation(2, 2));
} else {
ypr.y() = M_PI_2;
ypr.x() = -std::atan2(-rotation(1, 2), rotation(1, 1));
ypr.z() = 0.0;
}
} else {
ypr.y() = -M_PI_2;
ypr.x() = std::atan2(-rotation(1, 2), rotation(1, 1));
ypr.z() = 0.0;
}
return ypr;
}2. 轴角与旋转矩阵的变换关系
![]()

当已知旋转矩阵也可以得到旋转轴和旋转角:
![]()
![]()
旋转轴上的向量在旋转后不发生变化,即Rn=n
因此,旋转轴n为旋转矩阵R的特征值为1对应的特征向量。
旋转矩阵和旋转轴还可以写成如下形式:


3. 四元数转欧拉角
绕固定坐标系的X-Y-Z依次旋转α, β, γ角
则由四元数或
到欧拉角的转换为
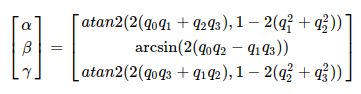
4. 四元数转旋转矩阵

5. 方向余弦矩阵

参考文献
四元数与欧拉角(RPY角)的相互转换 - XXX已失联 - 博客园
旋转矩阵(Rotation matrix):旋转轴与旋转角 ( axis and angle )_Sandy_WYM_的博客-CSDN博客_根据旋转矩阵求旋转轴的方向和旋转角度








 本文详细介绍了旋转矩阵与欧拉角之间的转换,包括从欧拉角到旋转矩阵以及从旋转矩阵到欧拉角的自定义转换函数,解决了Eigen库中可能出现的欧拉角跳变问题。此外,还讨论了旋转矩阵与旋转轴、旋转角的关系,以及四元数到欧拉角的转换方法。同时提供了四元数到旋转矩阵的转换,并提到了方向余弦矩阵在旋转描述中的应用。
本文详细介绍了旋转矩阵与欧拉角之间的转换,包括从欧拉角到旋转矩阵以及从旋转矩阵到欧拉角的自定义转换函数,解决了Eigen库中可能出现的欧拉角跳变问题。此外,还讨论了旋转矩阵与旋转轴、旋转角的关系,以及四元数到欧拉角的转换方法。同时提供了四元数到旋转矩阵的转换,并提到了方向余弦矩阵在旋转描述中的应用。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








