三维空间刚体运动4-1：四元数表示旋转（各形式相互转换加代码）

序：本篇系列文章参照高翔老师《视觉SLAM十四讲从理论到实践》，讲解三维空间刚体运动，为读者打下坚实的数学基础。博文将原第三讲分为五部分来讲解，其中四元数部分较多较复杂，又分为四部分。如果读者急于实践，可直接阅读第五部分的机器人运动轨迹，此部分详细讲解了安装准备工作。此系列总体目录如下：

1. 旋转矩阵和变换矩阵；
2. 旋转向量表示旋转；
3. 欧拉角表示旋转；
4. 四元数包括以下部分：
   4-1. 四元数表示变换；
   4-2. 四元数线性插值方法：LinEuler/LinMat/Lerp/Nlerp/Slerp；
   4-3. 四元数多点插值方法：Squad；
   4-4. 四元数多点连续解析解插值方法：Spicv；
   4-5. 四元数多点离散数值解插值方法：Sping。
5. 实践：SLAM中显示机器人运动轨迹及相机位姿。

1. 四元数的定义

1.1 为什么使用四元数

旋转矩阵用9个量描述3自由度的旋转，具有冗余性；欧拉角和旋转向量是紧凑的，但具有奇异性。事实上，我们找不到不带奇异性的三维向量描述方式。
回忆之前学习过的复数，我们用复数集$\mathbb{C}$表示复平面上的向量，可以表示为$z=a+bi$的形式，其中$a,b\in R$而且$i^2=-1$，而复数的乘法则表示复平面上的旋转：例如，乘上复数$i$相当于逆时针把一个复向量旋转$90^{\circ }$。类似的，在表达三维空间旋转时，也有一种类似于复数的代数：四元数（Quaternion）。四元数是Hamilton找到的一种扩展的复数。它既是紧凑的，也没有奇异性。如果说缺点，四元数不够直观，其运算稍复杂些。

1.2 复数与四元数

把四元数与复数类比可以帮助你更快地理解四元数。例如，当我们想要将复平面的向量旋转$\theta$角时，可以给这个复向量乘以$e^{i\theta }$，这是极坐标表示的复数，它也可以写成普通的形式，只要用欧拉公式即可：$$e^{i\theta }=cos\theta +isin\theta .$$
欧拉公式将指数函数的定义域扩大到了复数域，建立三角函数和指数函数的关系，被誉为“数学中的天桥”。欧拉公式的简单推导如下，$e^x$的泰勒展开式为：
$$e^x=1+x+\frac{1}{2!}{x}^2+\frac{1}{3!}{x}^3+\cdot \cdot \cdot$$将$x$替换为$i\theta$：
$$\begin{array}{rl}{e}^{i\theta }& =1+i\theta +\frac{1}{2!}(i\theta {)}^2+\frac{1}{3!}(i\theta {)}^3+\frac{1}{4!}(i\theta {)}^4+\frac{1}{5!}(i\theta {)}^5+\frac{1}{6!}(i\theta {)}^6+\frac{1}{7!}(i\theta {)}^7+\frac{1}{8!}(i\theta {)}^8+\cdot \cdot \cdot \\ & =1+i\theta -\frac{1}{2!}{\theta }^2-\frac{1}{3!}i{\theta }^3+\frac{1}{4!}{\theta }^4+\frac{1}{5!}i{\theta }^5-\frac{1}{6!}{\theta }^6-\frac{1}{7!}i{\theta }^7+\frac{1}{8!}{\theta }^8+\cdot \cdot \cdot \\ & =(1-\frac{{\theta }^2}{2!}+\frac{{\theta }^4}{4!}-\frac{{\theta }^6}{6!}+\frac{{\theta }^8}{8!}-\cdot \cdot \cdot )+i(\theta -\frac{{\theta }^3}{3!}+\frac{{\theta }^5}{5!}-\frac{{\theta }^7}{7!}+\cdot \cdot \cdot )\\ & =cos\theta +isin\theta .\end{array}$$当$\theta =\pi$时，带入欧拉公式得到：$$e^{i\pi }=cos\pi +isin\pi =-1\Rightarrow e^{i\pi }+1=0$$其中$e^{i\pi }+1=0$就是欧拉恒等式，它被誉为上帝公式，因为$e、\pi 、i$、乘法单位元1、加法单位元0，这五个重要的数学元素全部被包含在内，在数学爱好者眼里，它仿佛一行诗道尽了数学的美好。欧拉公式的详细说明可参见《欧拉公式之美》。
欧拉公式的右侧正是一个单位长度的复数，所以在二维情况下，旋转可以有单位复数来描述。类似的，可以看到，三维旋转可以有单位四元数来描述。

1.3 四元数的形式

四元数的定义和复数非常类似，唯一的区别就是四元数有三个虚部，而复数只有一个。所有的四元数$q\in \mathbb{H}$（$\mathbb{H}$代表四元数的发现者William Rowan Hamilton）都可以写成如下形式：$$\mathbf{q}=q_0+q_{1}i+q_{2}j+q_{3}k.$$其中$i,j,k$为四元数的三个虚部，这三个虚部满足以下关系式：$$\{\begin{array}{c}{i}^2=j^2=k^2=-1\\ ij=k,ji=-k\\ jk=i,kj=-i\\ ki=j,ik=-j\end{array}.$$
如果把$i,j,k$看成三个坐标轴，那么它们与自己的乘法和复数一样，相互之间的乘法和外积一样。有时，人们也用一个标量和一个向量来表达四元数：$$\mathbf{q}=[s,v{]}^T,s=q_0\in \mathbb{R},v=[q_1,q_2,q_3{]}^T\in {\mathbb{R}}^3.$$这里，$s$称为四元数的实部，而$v$称为它的虚部。如果一个四元数的虚部为0，则称为实四元数。反之，若实部为0，则称为虚四元数或纯四元数。
如果$\Vert q\Vert =1$，那么$q$是单位四元数。可以用单位四元数表示三维空间中任意一个旋转，不过这种表达方式和复数有着微妙的不同。在复数中，乘以$i$意味着旋转$90^{\circ }$，而在四元数中，乘以$i$对应着旋转$180^{\circ }$，这样才能保证$ij=k$的性质。而$i^2=-1$，意味着绕$i$轴旋转$360^{\circ }$后得到一个相反的东西，也就是要旋转两周才会和它原先的样子相等。
下面我们看一下四元数之间的运算法则。

2. 四元数的运算

四元数和复数一样，可以进行一系列的运算。常见的有四则运算、数乘、内外积、模长、共轭、求逆等，高阶运算有指数、对数、求微分等，下面分别介绍。
为了方便，这里给出三个定义：1）不包含四元数{[0,(0,0,0)]}的集合记为$\stackrel{\circ }{H}$；2）单位四元数集合记为${\mathbb{H}}_1$，它是$\stackrel{\circ }{H}$的子集；3）中元（neutral element)为：$I=[1,0]\in {\mathbb{H}}_1$，它使得：$qI=Iq=[1s,1v]=[s,v]=q$。

2.1 基础运算

现有四元数$q，q_a，q_b$，单元运算时使用$q$，否则使用$q_a,q_b$。它们的向量表示为$[s,v]，[s_a,v_a]$，$[s_b,v_b]$，其中$v=xi+yj+zk，v_a=x_{a}i+y_{a}j+z_{a}k，v_b=x_{b}i+y_{b}j+z_{b}k$，或者原始四元数表示为：$$q=s+xi+yj+zk，q_a=s_a+x_{a}i+y_{a}j+z_{a}k，q_b=s_b+x_{b}i+y_{b}j+z_{b}k.$$那么，其运算可表示如下：

1. 加法和减法$$q_a\pm q_b=[s_a\pm s_b,v_a\pm v_b]$$
2. 数乘
   又称标量乘法，四元数可以与数$k\in \mathbb{R}$相乘，$k$的四元数形式为$k=[k,0]$，故数乘可以表示为：$$kq=[k,0][s,v]=[ks,kv]$$
3. 内积或点积
   假设$q_a$和$q_b$之间的夹角为$\alpha$，则内积或点积定义为：$$\begin{array}{rl}{q}_a\cdot q_b& =\Vert q_a\Vert \Vert q_b\Vert \cos \alpha \\ & =s_a{s}_b+x_a{x}_b+y_a{y}_b+z_a{z}_b\end{array}$$
4. 外积或叉积
   一般意义的四元数乘法指的是外积或叉积，它是把$q_a$的每一项与$q_b$的每一项相乘，最后相加，整理得：$$\begin{array}{rl}{q}_a{q}_b& =s_a{s}_b-x_a{x}_b-y_a{y}_b-z_a{z}_b\\ & +(s_a{x}_b+x_a{s}_b+y_a{z}_b-z_a{y}_b)i\\ & +(s_a{y}_b-x_a{z}_b+y_a{s}_b+z_a{x}_b)j\\ & +(s_a{z}_b+x_a{y}_b-y_a{x}_b+z_a{s}_b)k.\end{array}$$虽然稍微复杂，但形式上还是整齐有序的。如果写成向量形式并利用内外积运算，该表达会更加简洁：$$q_a{q}_b=[s_a{s}_b-v_a^T{v}_b,s_a{v}_b+s_b{v}_a+v_a\times v_b]$$这个结果也称为$GraBmann$积，它是四元数与旋转联系起来的关键。
   另外，由于最后一项外积的存在，四元数乘法通常是不可交换的，除非$v_a$和$v_b$在$\mathbb{R}$中共线，此时外项积为零。
   不过对于同一个四元数，具有相乘和幂的性质：$$q^a{q}^b=q^{a+b},(q^a{)}^b=q^{ab},a,b\in \mathbb{R}$$
5. 模长或范数
   四元数的模长或范数定义为：$$\Vert q\Vert =\sqrt{q{q}^{\ast }}=\sqrt{s^2+x^2+y^2+z^2}$$可以验证，两个四元数乘积的模即模的乘积，这使得单位四元数相乘后仍是单位四元数：$$\Vert q_a{q}_b\Vert =\Vert q_a\Vert \Vert q_b\Vert$$
6. 共轭
   四元数的共轭是把虚部取成相反数：$$q^{\ast }=s-xi-yj-zk=[s,-v].$$四元数共轭与其本身相乘，会得到一个实四元数，其实部为模长的平方：$$q^{\ast }q=q{q}^{\ast }=[s^2+v^{T}v,0{]}^T$$此外，共轭的乘积满足以下性质：$$(q_a{q}_b{)}^{\ast }=q_b^{\ast }{q}_a^{\ast }$$
7. 逆
   四元数$q\in \stackrel{\circ }{H}$的逆为：$$q^{-1}=q^{\ast }/\Vert q\Vert$$按此定义，四元数和自己的逆的乘积为实四元数$1$：$$q{q}^{-1}=q^{-1}q=q{q}^{\ast }/{\Vert q\Vert }^2=1$$如果$\mathbf{q}$为单位四元数，其逆和共轭就是同一个量。同时，乘积的逆具有和矩阵相似的性质：$$(q_a{q}_b{)}^{-1}=q_b^{-1}{q}_a^{-1}$$

2.2 高阶运算

高阶运算包括对数、指数和微分运算，对数和指数在5.3节旋转证明完后再次引出定义，这里作为性质总结先做一下介绍，感兴趣的可以阅读后边证明。介绍高阶运算前，引入以下定理：
四元数定理1：设$q=[s,\mathbf{v}]\in {\mathbb{H}}_1$，那么存在${\mathbf{v}}^{{}^{\prime }}\in {\mathbb{R}}_1^3$和$\theta \in [-\pi ,\pi ]$，使得$q=[\cos \theta ,{\mathbf{v}}^{{}^{\prime }}\sin \theta ]$。
证明：如果$q=[1,0]$，使$\theta =0$，那么${\mathbf{v}}^{{}^{\prime }}$可以在${\mathbb{R}}^3$中的单位向量自由选择。
如果$q\ne [1,0]$，使$k=\left|\mathbf{v}\right|$，那么${\mathbf{v}}^{{}^{\prime }}=\frac{1}{k}\mathbf{v}$，这时$\mathbf{v}=k{\mathbf{v}}^{{}^{\prime }}$并且${\mathbf{v}}^{{}^{\prime }}$也是${\mathbb{R}}^3$中的单位向量，此时$q=[s,k{\mathbf{v}}^{{}^{\prime }}]$。由于$q$是一个单位四元数，因此可以得到：$$1=\Vert q\Vert =s^2+\mathbf{v}\cdot \mathbf{v}=s^2+k^2{\mathbf{v}}^{{}^{\prime }}\cdot {\mathbf{v}}^{{}^{\prime }}=s^2+k^2$$等式$s^2+k^2=1$代表平面中的圆，由于圆也可以表示为${\cos }^2\theta +{\sin }^2\theta =1$，因此存在$\theta \in [-\pi ,\pi ]$，使得$s=\cos \theta ,k=\sin \theta$，总之，我们会得到想要的结果：$$q=[s,\mathbf{v}]=[s,k{\mathbf{v}}^{{}^{\prime }}]=[\cos \theta ,{\mathbf{v}}^{{}^{\prime }}\sin \theta ]$$
接下来我们具体介绍四元数的高阶运算：

1. 对数
   使$q\in {\mathbb{H}}_1$，$q$表示为$[\cos \theta ,\mathbf{v}\sin \theta ],\theta \in \mathbb{R},\mathbf{v}\in {\mathbb{R}}^3,|\mathbf{v}|=1$，那么对数函数可以定义为：$$\log q\equiv [0,\theta \mathbf{v}]$$注意，根据定义存在$\log [1,(0,0,0)]=[0,(0,0,0)]$，并且$\log q$不是单位四元数。
2. 指数
   对于以下形式的四元数：$q=[0,\theta \mathbf{v}],\theta \in \mathbb{R},\mathbf{v}\in {\mathbb{R}}^3,|\mathbf{v}|=1$，指数函数被定义为：$$\exp q\equiv [\cos \theta ,\mathbf{v}\sin \theta ]$$注意：指数函数和对数函数可以互相转换，并且指数可以对应到单位四元数。
   从上面的定义可得到以下定义，对于$q^t,q\in {\mathbb{H}}_1,t\in \mathbb{R}$，它的指数方程形式：$$q^t=\exp (t\log q)$$此外当$q\in {\mathbb{H}}_1,t,a,b\in \mathbb{R}$还有其他性质，枚举如下（限于篇幅这里不再给出证明）：$$\log q^t=t\log q,q^a{q}^b=q^{a+b},(q^a{)}^b=q^{ab}$$
3. 微分
   此处给出常用的微分性质和证明，并将用于下一篇的四元数插值曲线的推导。
   （1）当指数为常数时的微分法则
   对于$q^t,q\in {\mathbb{H}}_1,t\in \mathbb{R}$，有：$$\frac{d}{dt}{q}^t=q^t\log (q)$$下边给出证明。
   公式左侧：$$\begin{array}{rl}\frac{d}{dt}{q}^t& =\frac{d}{dt}\exp (t\log (q))=\frac{d}{dt}\exp (t[0,\theta \mathbf{v}])\\ & =\frac{d}{dt}\exp ([0,t\theta \mathbf{v}])=\frac{d}{dt}[\cos (t\theta ),\sin (t\theta )\mathbf{v}]\\ & =\theta [-\sin (t\theta ),\sin (t\theta )\mathbf{v}]\end{array}$$公式右侧：$$\begin{array}{rl}{q}^t\log (q)& =\exp (t\log (q))\log (q)=[\cos (t\theta ),\sin (t\theta )\mathbf{v}][0,\theta \mathbf{v}]\\ & =[-\theta \sin (t\theta )(\mathbf{v}\cdot \mathbf{v}),\theta \cos (t\theta )\mathbf{v}+\theta \sin (t\theta )(\mathbf{v}\times \mathbf{v})]\\ & =[-\theta \sin (t\theta ),\theta \cos (t\theta )\mathbf{v}]\\ & =\theta [-\sin (t\theta ),\cos (t\theta )\mathbf{v}]\end{array}$$
   （2）当指数为函数时的微分法则
   在此之前，给出乘积微分法则和链式微分法则。
   乘积微分法则：使$f,g\in C^1(\mathbb{R},\mathbb{H})$，其中$C^1(\mathbb{R},\mathbb{H})$代表函数在定义域$\mathbb{R}$，值域$\mathbb{H}$范围内一阶连续可导，这时有：$$\frac{d}{dt}(f(t)g(t))=(\frac{d}{dt}f(t))g(t)+f(t)(\frac{d}{dt}g(t))$$
   链式微分法则：使$f\in C^1(\mathbb{H},\mathbb{H}),g\in C^1(\mathbb{R},\mathbb{H})$，这时有：$$\frac{d}{dt}(f(g(t))=f^{{}^{\prime }}(g(t))g^{{}^{\prime }}(t))$$
   当指数为函数时的微分法则:使$q\in C^1(\mathbb{R},{\mathbb{H}}_1),r\in C^1(\mathbb{R},\mathbb{R})$，由于$q$为单位四元数，所以$q(t)$可写为$[\cos \theta (t),\mathbf{v}(t)\sin \theta (t)]$，这时有：$$\begin{array}{rl}\frac{d}{dt}q(t{)}^{r(t)}& =\frac{d}{dt}\exp (r(t)\log (q(t)))\\ & =\frac{d}{dt}\exp (r(t)[0,\mathbf{v}(t)\theta (t)])\\ & =\frac{d}{dt}\exp ([0,r(t)\mathbf{v}(t)\theta (t)])\\ & =\frac{d}{dt}[\cos (r(t)\theta (t)),\sin (r(t)\theta (t))\mathbf{v}(t)]\\ & =[-\sin (r(t)\theta (t))(r^{{}^{\prime }}(t)\theta (t)+r(t){\theta }^{{}^{\prime }}(t)),\\ & \cos (r(t)\theta (t))(r^{{}^{\prime }}(t)\theta (t)+r(t){\theta }^{{}^{\prime }}(t))\mathbf{v}(t)+\sin (r(t)\theta (t)){\mathbf{v}}^{{}^{\prime }}(t)]\end{array}$$

3. 用四元数表示旋转

本节讲解四元数与旋转的关系，并给出几何证明。

3.1 四元数与旋转关系

我们可以用四元数表达对一个点的旋转。假设有一个空间三维点$v=[x,y,z]\in {\mathbb{R}}^3$，以及一个由单位四元数$q$指定的旋转。三维点$v$经过$q$的旋转后变为$v^{{}^{\prime }}$。如果使用矩阵描述，那么有$v^{{}^{\prime }}=Rv$。而如何用四元数描述旋转呢？
首先，把三维空间点用一个虚四元数来描述：$$w=[0,x,y,z{]}^T=[0,v{]}^T$$相当于把四元数的3个虚部和空间中的3个轴相对应。那么，旋转后的点$w^{{}^{\prime }}$可表示为这样的乘积：$$w^{{}^{\prime }}=qw{q}^{-1}$$这里的乘法均为四元数乘法，结果也是四元数。最后把$w^{{}^{\prime }}$的虚部取出，即得旋转之后点的坐标。并且可以验证，计算结果的实部为0，即为虚四元数。
下面从几何的角度进一步讲解四元数与3D旋转之间的关联。如果只是简单应用，不需要了解几何证明过程，则本小节就足够了。

3.2 四元数与3D旋转几何证明

回忆一下《旋转向量与罗德里格斯公式》讨论的内容：如果我们需要将一个向量$v$沿着一个用单位向量所定义的旋转轴$u$旋转$\theta$度，那么可以将其拆分为正交于旋转轴的$v_{\perp }$以及平行于旋转轴的$v_{\parallel }$，进行旋转后获得$v_{\perp }^{{}^{\prime }}$和$v_{\parallel }^{{}^{\prime }}$，相加后得到旋转后的结果$v^{{}^{\prime }}=v_{\perp }^{{}^{\prime }}+v_{\parallel }^{{}^{\prime }}$。
将这些向量定义为纯四元数，下标$q$代表三维空间变量对应的四元数：
$$\begin{array}{rlrl}& w=[0,v]& & w^{{}^{\prime }}=[0,v^{{}^{\prime }}]\\ & w_{\perp }=[0,v_{\perp }]& & w_{\perp }^{{}^{\prime }}=[0,v_{\perp }^{{}^{\prime }}]\\ & w_{\parallel }=[0,v_{\parallel }]& & w_{\parallel }^{{}^{\prime }}=[0,v_{\parallel }^{{}^{\prime }}]\\ & u_q=[0,u]& & \end{array}$$那么我们就能得到：$$\begin{array}{rlr}w=w_{\perp }+w_{\parallel }& & w^{{}^{\prime }}=w_{\perp }^{{}^{\prime }}+w_{\parallel }^{{}^{\prime }}\end{array}$$和之前一样，这里也分开讨论$w_{\perp }$和$w_{\parallel }$的情况。

3.2.1 $w_{\perp }$的旋转

之前推导过（见《旋转向量与罗德里格斯公式》第2.2.1节），如果一个向量$v_{\perp }$正交于旋转轴$u$，那么$$v_{\perp }^{{}^{\prime }}=cos(\theta )v_{\perp }+sin(\theta )(u\times v_{\perp })$$将三维向量替换为对应的四元数，$v_{\perp }^{{}^{\prime }}$和$v_{\perp }$可以直接替换，而对于$u\times v_{\perp }$，由于$$\begin{array}{rl}{u}_q{w}_{\perp }& =[-u\cdot v_{\perp },u\times v_{\perp }]\\ & =[0,u\times v_{\perp }]\\ & =u\times v_{\perp }\end{array}$$将之前定义的四元数带入，就能得到$$w_{\perp }^{{}^{\prime }}=cos(\theta )w_{\perp }+sin(\theta )(u_q{w}_{\perp })$$因为四元数遵守分配率，可以继续变换这个等式：$$w_{\perp }^{{}^{\prime }}=(cos(\theta )+sin(\theta )u_q)w_{\perp }$$此时，可以将$cos(\theta )+sin(\theta )u_q$看作一个四元数，记为$q$，且$\Vert q\Vert =1$（读者可以自证，用到$\Vert u\Vert =1$），这样我们就能将旋转写成四元数的乘积了。到此为止，我们已经将旋转与四元数的积联系起来了，由此得到$$w_{\perp }^{{}^{\prime }}=q{w}_{\perp }$$也就是说，如果旋转轴$u$的坐标为$u=\left[\begin{array}{c}{u}_x\\ u_y\\ u_z\end{array}\right]$，旋转角为$\theta$，那么完成这一旋转所需要的四元数$q$可以构造为：$$\begin{array}{rl}q& =cos(\theta )+sin(\theta )u_q\\ & =[cos(\theta ),0]+[0,sin(\theta )u]\\ & =[cos(\theta ),sin(\theta )u]\\ & =cos(\theta )+sin(\theta )u_{x}i+sin(\theta )u_{y}j+sin(\theta )u_{z}k\end{array}$$总结一下，得到定理3D旋转公式（正交四元数型）：当$v_{\perp }$正交于旋转轴$u$时，旋转$\theta$角度之后的$v_{\perp }^{{}^{\prime }}$可以使用$v_{\perp }$的对应四元数与四元数$q$相乘来获得。令$w_{\perp }=[0,v_{\perp }],w_{\perp }^{{}^{\prime }}=[0,v_{\perp }^{{}^{\prime }}],q=[cos(\theta ),sin(\theta )u]$，那么：$$w_{\perp }^{{}^{\prime }}=q{w}_{\perp }$$

3.2.2 $w_{\parallel }$的旋转

接下来是平行于旋转轴的$w_{\parallel }$。之前已经讨论过，如果一个向量$v_{\parallel }$平行于$u$，那么旋转$\theta$后对它不会做出任何变换，由此得到定理3D旋转公式（平行四元数型）：当$v_{\parallel }$平行于旋转轴$u$时，旋转$\theta$角度之后的$v_{\parallel }^{{}^{\prime }}$用四元数可以写为：$$w_{\parallel }^{{}^{\prime }}=w_{\parallel }$$

3.2.3 $w$的旋转

有了前面的结论，我们可以获得一般情况下$w^{{}^{\prime }}$的结果了：$$\begin{array}{rl}{w}^{{}^{\prime }}& =w_{\parallel }^{{}^{\prime }}+w_{\perp }^{{}^{\prime }}\\ & =w_{\parallel }+q{w}_{\perp }\end{array}$$在进一步化简之前，引入三个引理：

1. 四元数引理1 ：如果$q=[cos(\theta ),sin(\theta )u]$，而且$u$为单位向量，那么$q^2=qq=[cos(2\theta ),sin(2\theta )u]$。
2. 四元数引理2 ：假设$w_{\parallel }=[0,v_{\parallel }]$是一个纯四元数，而$q=[\alpha ,\beta u]$，其中$u$是一个单位向量，$\alpha ,\beta \in \mathbb{R}$。在这种条件下，如果$v_{\parallel }$平行于$u$，那么$q{w}_{\parallel }=w_{\parallel }q$。
3. 四元数引理3 ：假设$w_{\perp }=[0,v_{\perp }]$是一个纯四元数，而$q=[\alpha ,\beta u]$，其中$u$是一个单位向量，$\alpha ,\beta \in \mathbb{R}$。在这种条件下，如果$v_{\perp }$垂直于$u$，那么$q{w}_{\perp }=w_{\perp }{q}^{\ast }$。

关于引理的证明，读者可以参考文献2，这里不再扩展。
为方便证明，再引入一个新的四元数$p=[cos(\frac{1}{2}\theta ),sin(\frac{1}{2}\theta )u]$，$q=p^2$，$\Vert p\Vert =1$。现在，我们就能对原本的旋转公式进行变形了：$$\begin{array}{rl}{w}^{{}^{\prime }}& =w_{\parallel }+q{w}_{\perp }\\ & =p{p}^{-1}{w}_{\parallel }+pp{w}_{\perp }\\ & =p{p}^{\ast }{w}_{\parallel }+pp{w}_{\perp }\\ & =p{w}_{\parallel }{p}^{\ast }+p{w}_{\perp }{p}^{\ast }\\ & =p(w_{\parallel }+w_{\perp })p^{\ast }\\ & =p{w}_{}{p}^{\ast }\end{array}$$至此，我们就解开了四元数与3D旋转之间的谜题。3D空间中任意一个旋转都能够用三个四元数相乘的形式表达出来。
综上，我们可以总结出一个定理3D旋转公式（一般情况四元数型）：任意向量$v$沿着以单位向量定义的旋转轴$u$旋转$\theta$度之后的$v^{{}^{\prime }}$，可以使用四元数乘法来获得。令$w=[0,v],w^{{}^{\prime }}=[0,v^{{}^{\prime }}]q=[cos(\frac{1}{2}\theta ),sin(\frac{1}{2}\theta )u]$，那么：$$w^{{}^{\prime }}=qw{q}^{\ast }=qw{q}^{-1}$$这里用的是$\frac{1}{2}\theta$而不是$\theta$。这是因为$q$做的就是一个$\frac{1}{2}\theta$的旋转，而$q^{\ast }$或$q^{-1}$也做了一个$\frac{1}{2}\theta$的旋转。我们进行了两次旋转，而不是一次，这两次旋转的结果是一个旋转角为$\theta$的旋转。下图或可解释旋转的过程：
注释：对$w^{{}^{\prime }}=qw{q}^{\ast }=qw{q}^{-1}$，可以这样理解：对向量$v$转化成的纯四元数$w$，经过$q$的旋转$qw$后，得到实部不为0的普通四元数，这时没办法映射到三维超平面（总不能转着圈就转到了四维空间吧），结果与最初的点不在同一三维空间。为了解决这个问题，先对第四维（角度）旋转一半，再用逆或共轭反转回来，这时正好将产生的第四维变为0，重新回到初始的三维超平面空间。这样不仅解决了奇点问题，也不会产生冗余数据，不知道$Hamilton$怎么想到的，总之很佩服。

4. 四元数到其它旋转表示的相互转换

任意单位四元数描述了一个旋转，该旋转也可用旋转向量、旋转矩阵或欧拉角描述。现在来考察四元数与旋转向量、旋转矩阵以及欧拉角的相互转换关系。

4.1 旋转向量

本节介绍旋转向量与四元数之间的转换关系。
绕坐标轴的多次旋转可以等效为绕某一转轴旋转一定的角度。假设已知等效旋转轴方向单位旋转向量$u$的坐标为$u=\left[\begin{array}{c}{u}_x\\ u_y\\ u_z\end{array}\right]$，旋转角为$\theta$。根据3.2.3推导的定理3D旋转公式（一般情况四元数型），设其等效的单位四元数为$q=[q_0,q_1,q_2,q_3]$，则有：$$\{\begin{array}{c}{q}_0=cos(\frac{1}{2}\theta )\\ q_1=u_{x}sin(\frac{1}{2}\theta )\\ q_2=u_{y}sin(\frac{1}{2}\theta )\\ q_3=u_{z}sin(\frac{1}{2}\theta )\end{array}\text{\hspace{1em}(4.1)}$$
同理，当已知单位四元数$q=[q_0,q_1,q_2,q_3]$，其对应的旋转角$\theta$和旋转向量$u$为：$$\{\begin{array}{c}\theta =2\arccos q_0\\ [u_x,u_y,u_z{]}^T=[q_1,q_2,q_3{]}^T/\sin (\frac{2}{\theta })\end{array}\text{\hspace{1em}(4.2)}$$

4.2 旋转矩阵

已知单位四元数$q$，根据博文《三维空间刚体运动2：旋转向量与罗德里格斯公式》中的罗德里格斯公式展开式（2.3）及本文公式（4.2），将单位旋转向量$u$及旋转角$\theta$替换为单位四元数$q$，省去计算过程，得到单位四元数到旋转矩阵的转换公式为：$$R=\left[\begin{array}{ccc}1-2q_2^2-2q_3^2& 2(q_1{q}_2-q_0{q}_3)& 2(q_1{q}_3+q_0{q}_2)\\ 2(q_1{q}_2+q_0{q}_3)& 1-2q_1^2-2q_3^2& 2(q_2{q}_3-q_0{q}_1)\\ 2(q_1{q}_3-q_0{q}_2)& 2(q_2{q}_3+q_0{q}_1)& 1-2q_1^2-2q_2^2\end{array}\right]\text{\hspace{1em}(4.3)}$$
假设已知变换矩阵：$$R=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]$$根据公式（4.3），推导对应的单位四元数为：$$\{\begin{array}{c}{q}_0=\frac{1}{2}\sqrt{1+r_{11}+r_{22}+r_{33}}\\ q_1=\frac{r_{32}-r_{23}}{4q_0}\\ q_2=\frac{r_{13}-r_{31}}{4q_0}\\ q_3=\frac{r_{21}-r_{12}}{4q_0}\end{array}\text{\hspace{1em}(4.4)}$$

4.3 欧拉角

4.3.1 转换关系

那么将Z-Y-X欧拉角（或RPY角：绕固定坐标系的X-Y-Z依次旋转α,β,γ角）转换为四元数：$$q=\left[\begin{array}{c}\cos \frac{\gamma }{2}\\ 0\\ 0\\ \sin \frac{\gamma }{2}\end{array}\right]\left[\begin{array}{c}\cos \frac{\beta }{2}\\ 0\\ \sin \frac{\beta }{2}\\ 0\end{array}\right]\left[\begin{array}{c}\cos \frac{\alpha }{2}\\ \sin \frac{\alpha }{2}\\ 0\\ 0\end{array}\right]=\left[\begin{array}{c}\cos \frac{\alpha }{2}\cos \frac{\beta }{2}\cos \frac{\gamma }{2}+\sin \frac{\alpha }{2}\sin \frac{\beta }{2}\sin \frac{\gamma }{2}\\ \sin \frac{\alpha }{2}\cos \frac{\beta }{2}\cos \frac{\gamma }{2}-\cos \frac{\alpha }{2}\sin \frac{\beta }{2}\sin \frac{\gamma }{2}\\ \cos \frac{\alpha }{2}\sin \frac{\beta }{2}\cos \frac{\gamma }{2}+\sin \frac{\alpha }{2}\cos \frac{\beta }{2}\sin \frac{\gamma }{2}\\ \cos \frac{\alpha }{2}\cos \frac{\beta }{2}\sin \frac{\gamma }{2}-\sin \frac{\alpha }{2}\sin \frac{\beta }{2}\cos \frac{\gamma }{2}\end{array}\right]$$
根据上面的公式可以求出逆解，即由四元数$q=(q_0,q_1,q_2,q_3)$到欧拉角的转换为：$$\left[\begin{array}{c}\alpha \\ \beta \\ \gamma \end{array}\right]=\left[\begin{array}{c}atan2(2(q_0{q}_1+q_2{q}_3),1-2(q_1^2+q_2^2))\\ \arcsin (2(q_0{q}_2-q_1{q}_3)\\ atan2(2(q_0{q}_3+q_1{q}_2),1-2(q_2^2+q_3^2))\end{array}\right]$$这里使用了$atan2(y,x)$而不是$arctan(\frac{y}{x})$，因为$arctan(\frac{y}{x})$的取值范围为$[-\frac{\pi }{2},\frac{\pi }{2}]$，只有$180°$，而绕某个轴旋转时范围是$360°$，$atan2(y,x)$正好满足需求。$atan2(y,x)$是一个函数，在C语言里返回的是指方位角，函数原型为$doubleatan2(doubley,doublex)$ ，返回以弧度表示的 $y/x$ 的反正切。y 和 x 的值的符号决定了正确的象限。也可以理解为计算复数$x+yi$ 的辐角，计算时atan2 比 atan 稳定。

4.3.2 转换中的万象锁问题

另外需要注意的就是奇异性问题，即万向锁，下面分析这种情况。当刚体绕Y轴旋转了$90°$（俯仰角pitch=90）时，如何计算横滚角roll和偏航角yaw？这时会发生自由度丢失的情况，即Yaw和Roll会变为一个自由度。此时再使用上面的公式根据四元数计算欧拉角会出现问题：$\arcsin (2(q_0{q}_2-q_1{q}_3)$的定义域为$[-1,1]$，当$2(q_0{q}_2-q_1{q}_3)=\pm 0.5$时（在程序中浮点数不能直接进行等于判断，要使用合理的阈值），俯仰角$\beta$为$\pm 90°$，将其带入正向公式计算出四元数$(q_0,q_1,q_2,q_3)$，然后可以发现逆向公式中atan2函数中的参数全部为0，即出现了$\frac{0}{0}$的情况！无法计算。
当$\beta =90°$时，$\sin \frac{\beta }{2}=\cos \frac{\beta }{2}=0.707$，将其带入公式中有：$$q=\left[\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\end{array}\right]=\left[\begin{array}{c}0.707(\cos \frac{\alpha }{2}\cos \frac{\gamma }{2}+\sin \frac{\alpha }{2}\sin \frac{\gamma }{2})\\ 0.707(\sin \frac{\alpha }{2}\cos \frac{\gamma }{2}-\cos \frac{\alpha }{2}\sin \frac{\gamma }{2})\\ 0.707(\cos \frac{\alpha }{2}\cos \frac{\gamma }{2}+\sin \frac{\alpha }{2}\sin \frac{\gamma }{2})\\ 0.707(\cos \frac{\alpha }{2}\sin \frac{\gamma }{2}-\sin \frac{\alpha }{2}\cos \frac{\gamma }{2})\end{array}\right]=\left[\begin{array}{c}0.707\cos \frac{\alpha -\gamma }{2}\\ 0.707\sin \frac{\alpha -\gamma }{2}\\ 0.707\cos \frac{\alpha -\gamma }{2}\\ -0.707\sin \frac{\alpha -\gamma }{2}\end{array}\right]$$则$\frac{q_1}{q_0}=-\frac{q_3}{q_2}=\tan \frac{\alpha -\gamma }{2}$，于是有：$$\alpha -\gamma =2atan2(q_1,q_0)$$通常令$\alpha =0$，这时$\gamma =-2atan2(q_1,q_0)$。当俯仰角$\beta$为-90°，即刚体竖直向下时的情况也与之类似，可以推导出奇异姿态时的计算公式。
将四元数转换为欧拉角的代码可以参考附件。需要注意欧拉角有12种旋转次序，而上面推导的公式是按照Z-Y-X顺序进行的，所以有时会在网上看到不同的转换公式（因为对应着不同的旋转次序），在使用时一定要注意旋转次序是什么。比如ADAMS软件里就默认Body 3-1-3次序，即Z-X-Z欧拉角，而VREP中则按照X-Y-Z欧拉角旋转。另外万向锁问题代码的Z-Y-X欧拉角代码见类CameraSpacePoint。

5. 四元数的其他性质

为更全面理解四元数和方便引入slerp插值，这一节补充四元数的其它性质：旋转复合、双倍覆盖和指数形式。

5.1 旋转的复合

旋转的复合其实在我们之前证明$q^2=qq=[cos(2\theta ),sin(2\theta )u]$的时候就已经涉及到一点了，但是这里我们考虑的是更一般的情况。
假设有两个表示沿着不同轴、不同角度旋转的四元数$q_1、q_2$。首先，我们实施 $q_1$的变换，变换之后的$v^{{}^{\prime }}$为$$v^{{}^{\prime }}=q_{1}v{q}_1^{\ast }$$接下来，对$v^{{}^{\prime }}$进行$q_2$的变换，得到$v^{{}^{\prime \prime }}$：$$v^{{}^{\prime \prime }}=q_2{v}^{{}^{\prime }}{q}_2^{\ast }=q_2{q}_{1}v{q}_1^{\ast }{q}_2^{\ast }=q_{net}v{q}_{net}^{\ast }$$其中$q_{net}=q_2{q}_1$，另外写成上面的形式，还用到性质$q_1^{\ast }{q}_2^{\ast }=(q_2{q}_1{)}^{\ast }$。
注意四元数乘法的顺序，这和矩阵、复数的复合非常相似，都是从右向左叠加。另外要注意的是，$q_1$与$q_2$的等价旋转$q_{net}$并不是沿着$q_1$与$q_2$的两个旋转轴进行的两次旋转，它是沿着一个全新的旋转轴进行的一个等价旋转，仅仅只有旋转的结果相同。

5.2 双倍覆盖

四元数与 3D 旋转的关系并不是一对一的，同一个 3D 旋转可以使用两个不同的四元数来表示．对任意的单位四元数$q=[cos(\frac{1}{2}\theta ),sin(\frac{1}{2}\theta )u]$，$q$与$-q$代表的是同一个旋转。如果$q$表示的是沿着旋转轴$u$旋转$\theta$度，那么$-q$代表的是沿着相反的旋转轴$-u$旋转$(2\pi -\theta )$，负负得正：$$\begin{array}{rl}-q& =[-cos(\frac{1}{2}\theta ),-sin(\frac{1}{2}\theta )u]\\ & =[cos(\pi -\frac{1}{2}\theta ),sin(\pi -\frac{1}{2}\theta )(-u)]\end{array}$$所以，这个四元数旋转的角度为$2(\pi -\frac{1}{2}\theta )=2\pi -\theta$，从下面的图中我们可以看到，这两个旋转是完全等价的：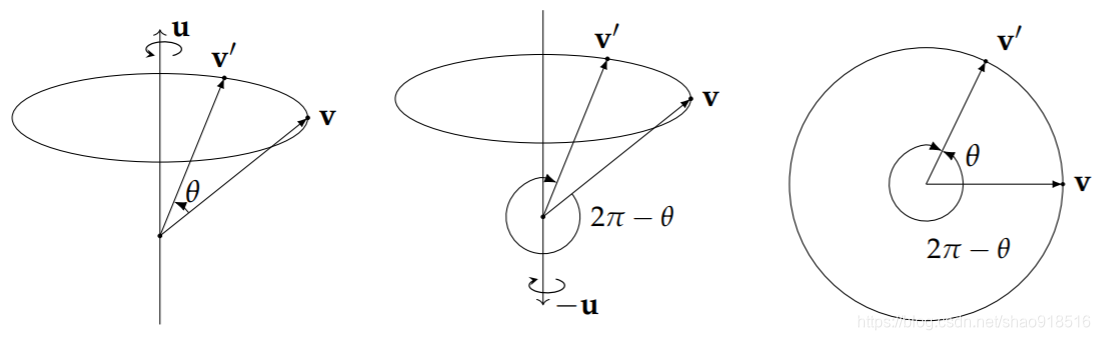
其实从四元数的旋转公式中也能推导出相同的结果：$$(-q)v(-q{)}^{\ast }=(-1{)}^{2}qv{q}^{\ast }=qv{q}^{\ast }$$所以，我们经常说单位四元数与3D旋转有一个「2对1满射同态」(2-1 Surjective Homomorphism) 关系，或者说单位四元数双倍覆盖(Double Cover)了3D旋转。它的严格证明会用到一些李群的知识，这里不再拓展。
有一点需要注意的是，虽然$q$与$-q$是两个不同的四元数，但是由于旋转矩阵中的每一项都包含了四元数两个分量的乘积，它们的旋转矩阵是完全相同的，即旋转矩阵并不会出现双倍覆盖的问题。

5.3 指数形式

在讨论复数的时候，我们利用欧拉公式将2D的旋转写成了$v^{{}^{\prime }}=e^{i\theta v}$这样的指数形式。实际上，我们也可以利用四元数将 3D 旋转写成类似的形式。
类似于复数的欧拉公式，四元数也有一个类似的公式。如果$u$是一个单位向量，那么对于单位四元数$u_q=[0,u]$，有：$$e^{u\theta }=cos(\theta )+u_{q}sin(\theta )=cos(\theta )+usin(\theta )$$这也就是说，$q=[\cos (\theta ),\sin (\theta )u]$可以使用指数表示为$e^{u\theta }$。这个公式的证明与欧拉公式的证明非常类似，直接使用级数展开就可以了，这里不再扩展。
注意，因为$u$是一个单位向量，$u^2=[-u\cdot u,0]=-\Vert u{\Vert }^2=-1$．这与欧拉公式中的$i$是非常类似的。有了指数型的表示方式，我们就能够将之前四元数的旋转公式改写为指数形式了，由此可得到定义：
3D旋转公式（指数型）：任意向量$v$沿着以单位向量定义的旋转轴$u$旋转$\theta$角度之后的$v^{{}^{\prime }}$可以使用四元数的指数表示。令$w=[0,v],u_q=[0,u]$，那么：$$w^{{}^{\prime }}=e^{u_q\frac{\theta }{2}}v{e}^{-u_q\frac{\theta }{2}}$$有了四元数的指数定义，我们就能够定义四元数的更多运算了。首先是自然对数$log$，对任意单位四元数$q=[cos(\theta ),sin(\theta )u]=e^{u_q\theta }$：$$log(q)=log(e^{u_q\theta })=[0,u\theta ]$$接下来是单位四元数的幂运算：$$q^t=(e^{u_q\theta }{)}^t=e^{u_q(t\theta )}=[cos(t\theta ),sin(t\theta )u]$$可以看到，一个单位四元数的$t$次幂等同于将它的旋转角度缩放至$t$倍，并且不会改变它的旋转轴（$u$必须是单位向量，所以一般不能与$t$结合）。这些运算会在之后讨论四元数插值时非常有用。限于篇幅，四元数插值的讲解见下一篇博客《三维空间刚体运动4-2：四元数插值（lerp，Nlerp，Slerp，Squad等）》

5.4 幂函数性质

上面给出四元数的指数形式后，可推导出一个重要的指函数性质，这一性质下一篇将用到。首先看推论：
四元数推论1 ：设$q\in {\mathbb{H}}_1,p=[a,b\mathbf{v}]$，其中$a,b,r\in \mathbb{R},\mathbf{v}\in {\mathbb{R}}^3$，如果$q[r,\mathbf{v}]q^{\ast }=[r,{\mathbf{v}}^{{}^{\prime }}]$，那么$q[a,b\mathbf{v}]q^{\ast }=[a,b{\mathbf{v}}^{{}^{\prime }}]$。
推论证明：$$\begin{array}{rl}qp{q}^{\ast }& =q[a,b\mathbf{v}]q^{\ast }\\ & =qb[\frac{a}{b},\mathbf{v}]q^{\ast }\\ & =b[\frac{a}{b},{\mathbf{v}}^{{}^{\prime }}]\\ & =[a,b{\mathbf{v}}^{{}^{\prime }}]\end{array}$$根据推论，得出以下定理：
四元数定理2 ：设$q,p\in {\mathbb{H}}_1,p=[\cos \theta ,\sin \theta \mathbf{v}],t\in \mathbb{R}$，那么$q{p}^t{q}^{\ast }=(qp{q}^{\ast }{)}^t$。
定理证明：
根据推论，存在${\mathbf{v}}^{{}^{\prime }}\in {\mathbb{R}}^3$，使得$q[\cos \theta ,\sin \theta \mathbf{v}]q^{\ast }=[\cos \theta ,\sin \theta {\mathbf{v}}^{{}^{\prime }}]$，因此得到：$$\begin{array}{rl}q{p}^t{q}^{\ast }& =q(\exp (t\log p))q^{\ast }\\ & =q(\exp (t[0,\theta \mathbf{v}]))q^{\ast }\\ & =q(\exp [0,t\theta \mathbf{v}])q^{\ast }\\ & =q([\cos t\theta ,\sin t\theta \mathbf{v}])q^{\ast }\\ & =[\cos t\theta ,\sin t\theta {\mathbf{v}}^{{}^{\prime }}]\\ & =\exp (t[0,\theta {\mathbf{v}}^{{}^{\prime }}])\\ & =\exp (t\log [\cos \theta ,\sin \theta {\mathbf{v}}^{{}^{\prime }}])\\ & =\exp (t\log (qp{q}^{\ast }))\\ & =(qp{q}^{\ast }{)}^t\end{array}$$
至此，四元数表示旋转的理论部分讲解完了。

6. 实践

现在，我们通过两个小程序实际演练四元数的运算。其中四元数的基础运算和高阶运算程序实现放在下一讲Slerp中。

6.1 四元数旋转运算

第一个小程序是演示四元数的常规运算，包括与旋转矩阵、旋转向量的转换，以及用四元数旋转一个向量，如下所示：

#include<iostream>
#include<cmath>
using namespace std;

#include<eigen3/Eigen/Core>
#include<eigen3/Eigen/Geometry>

using namespace Eigen;

int main(int argc, char **argv){
    //Eigen/Geometry模块提供了各种旋转和平移的表示，3D旋转矩阵直接使用Matrix3d或Matrix3f
    Matrix3d rotation_matrix = Matrix3d::Identity();
    //旋转向量使用AngleAxis，它底层不直接是Matrix，但运算可以当做矩阵，因为重载了运算符
    AngleAxisd rotation_vector(M_PI/4, Vector3d(0, 0, 1));
    //设置输出精度
    cout.precision(3);
    cout<<"rotation matrix =\n"<<rotation_matrix<<endl;
    cout<<"rotation vector =\n"<<rotation_vector.matrix()<<endl;
    
    //旋转向量转换的矩阵可以直接赋值给旋转矩阵
    rotation_matrix = rotation_vector.toRotationMatrix();
    cout<<"rotation vector to Matrix =\n"<<rotation_matrix<<endl;
    
    //旋转向量
    Vector3d v(1, 0, 0);
    cout<<"v = "<<v.transpose()<<endl;
    
	//四元数，可以直接把AngleAxis赋值给四元数，反之亦然
    Quaterniond q = Quaterniond(rotation_vector);
    //coeffs:多项式系数（coefficients)，其顺序为(x,y,z,w)，w为实部，xyz为虚部
    cout<<"quaternion from rotation vector = "<<q.coeffs().transpose()<<endl;
    //也可以直接把旋转矩阵赋给它
    q = Quaterniond(rotation_matrix);
    cout<<"quaternion from rotation matrix = "<<q.coeffs().transpose()<<endl;
    //使用四元数旋转一个向量，使用重载的乘法即可
    //注意q*v在数学上是qvq^{-1}
    v_rotated = q*v;
    cout<<"(1,0,0) after rotation = "<<v_rotated.transpose()<<endl;
    //用常规向量乘法表示qvq^{-1}，则计算如下：
    Quaterniond q_rotate_v = q*Quaterniond(0,1,0,0)*q.inverse();
    cout<<"should be equal to "<<q_rotate_v.coeffs().transpose()<<endl;
    
    return 0;

输出结果如下：

rotation matrix =
1 0 0
0 1 0
0 0 1
rotation vector =
 0.707 -0.707      0
 0.707  0.707      0
     0      0      1
rotation vector to Matrix =
 0.707 -0.707      0
 0.707  0.707      0
     0      0      1
v = 1 0 0
v transofrmed = 1.71 3.71    4
quaternion from rotation vector =     0     0 0.383 0.924
quaternion from rotation matrix =     0     0 0.383 0.924
(1,0,0) after rotation = 0.707 0.707     0
should be equal to 0.707 0.707     0     0

请读者注意，程序代码通常和数学表示有一些细微的差别。例如，通过运算符重载，四元数和三维向量可以直接计算乘法，但在数学上则需要先把向量转成虚四元数，再利用四元数乘法进行计算，同样的情况也适用于变换矩阵乘三维向量的情况。总体而言，程序中的用法会比数学公式更灵活。

6.2 坐标变换

下面我们举一个小例子来演示坐标变换。
例子：设有小萝卜一号和小萝卜二号位于世界坐标系中。记世界坐标系为$W$，小萝卜们的坐标系分别为$R_1$和$R_2$。小萝卜一号的位姿为$q_1=[0.35,0.2,0.3,0.1{]}^T$，$t_1=[0.3,0.1,0.1{]}^T$。小萝卜二号的位姿为$q_2=[-0.5,0.4,-0.1,0.2{]}^T$，$t_2=[-0.1,0.5,0.3{]}^T$。这里的$q$和$t$表达的是$T_{R_k,W},k=1,2$，也就是世界坐标系到相机坐标系的变换关系。现在，小萝卜一号看到某个点在自身的坐标系下坐标为$p_{R_1}=[0.5,0,0.2{]}^T$，求该向量在小萝卜二号坐标系下的坐标。
这是一个非常简单，但又具有代表性的例子。在实际场景中你经常需要在同一个机器人的不同部分，或者不同机器人之间转换坐标。计算过程也很简单，只需计算：$$p_{R_2}=T_{R_2,W}{T}_{W,R_1}{p}_{R_1}$$下面请看程序：

#include<iostream>
#include<vector>
#include<algorithm>
#include<eigen3/Eigen/Core>
#include<eigen3/Eigen/Geometry>

using namespace std;
using namespace Eigen;

int main(int argc, char** argv){
    //位姿四元数q1,q2
    Quaterniond q1(0.35, 0.2, 0.3, 0.1), q2(-0.5, 0.4, -0.1, 0.2);
    cout<<"q1.coeffs=\n"<<q1.coeffs()<<endl;
    cout<<"q2.coeffs=\n"<<q2.coeffs()<<endl;
    
    //四元数转换为旋转矩阵
    cout<<"q1.matrix=\n"<<q1.matrix()<<endl;
    cout<<"q2.matrix=\n"<<q2.matrix()<<endl;
    //归一化，转换为单位四元数
    q1.normalize();
    q2.normalize();
    cout<<"q1.normalize="<<q1.matrix()<<endl;
    cout<<"q2.normalize="<<q2.matrix()<<endl;
    //位移向量t1,t2,小萝卜一号下的坐标pr1
    Vector3d t1(0.3, 0.1, 0.1), t2(-0.1, 0.5, 0.3);
    Vector3d pr1(0.5, 0, 0.2);
    
    //Eigen::Isometry3d:欧式变换矩阵4*4
    Isometry3d Twr1(q1), Tr2w(q2);
    cout<<"Twr1.matrix="<<Twr1.matrix()<<endl;
    cout<<"Tr2w.matrix="<<Tr2w.matrix()<<endl;
    //坐标转换，计算T=Ra+t
    Twr1.pretranslate(t1);
    Tr2w.pretranslate(t2);
    
    //先将pr1转换为世界坐标系，然后转换为小萝卜二号下的坐标pr2
    Vector3d pr2 = Tr2w * Twr1.inverse()*pr1;
    cout<<"pr2.transpose="<<pr2.transpose()<<endl;
    
    return 0;
}

输出结果如下：

q1.coeffs=
 0.2
 0.3
 0.1
0.35
q2.coeffs=
 0.4
-0.1
 0.2
-0.5
q1.matrix=
  0.8  0.05  0.25
 0.19   0.9 -0.08
-0.17   0.2  0.74
q2.matrix=
  0.9  0.12  0.26
-0.28   0.6  0.36
 0.06 -0.44  0.66
q1.normalize=
  0.238095   0.190476   0.952381
   0.72381   0.619048  -0.304762
 -0.647619   0.761905 0.00952381
q2.normalize=
 0.782609   0.26087  0.565217
-0.608696  0.130435  0.782609
 0.130435 -0.956522   0.26087
Twr1.matrix=
  0.238095   0.190476   0.952381          0
   0.72381   0.619048  -0.304762          0
 -0.647619   0.761905 0.00952381          0
         0          0          0          1
Tr2w.matrix=
 0.782609   0.26087  0.565217         0
-0.608696  0.130435  0.782609         0
 0.130435 -0.956522   0.26087         0
        0         0         0         1
pr2.transpose=
-0.0309731    0.73499   0.296108

四元数的第一部分讲解到此。

本文基于《视觉SLAM十四讲：从理论到实践》和《Quaternions, Interpolation and Animation》编写，但相对于原文会适当精简，同时为便于全面理解，会收集其他网络好文，根据作者理解，加入一些注解和扩展知识点，如果您觉得还不错，请一键四连（点赞关注收藏评论），让更多的人看到。

参考文献：

1. 《视觉SLAM十四讲：从理论到实践》，高翔、张涛等著，中国工信出版社
2. Quaternions, Interpolation and Animation
3. 四元数与三维旋转
4. 四元数与欧拉角（RPY角）的相互转换
5. 如何形象地理解四元数？